当前，数据成为核心生产要素，企业将消费者信息整合成为大数据，对消费者偏好加以搜集、整理、研究的能力在市场竞争中变得愈发重要^[1]。企业利用这些数据对消费者群体进行建模，并采用“一人一价”定制化价格，但同时也带来了“大数据杀熟”价格歧视问题^[2-4]。加剧消费者隐私泄露风险的同时，也降低了消费者对网络交易市场的信任^[5]。随着消费者个人信息保护意识的增强，国家也出台相关政策法规对个人信息进行保护，如2021年颁布的《中华人民共和国个人信息保护法》，使企业搜集信息的难度及成本发生变化，影响着企业产品定价决策。据此，本文在大数据背景下以两类制造商为主体，通过建立制造商定价策略的双群体演化博弈模型，研究制造商定价策略的动态演化及其影响机理。

与本文研究相关的文献主要有两类，一是关于歧视性定价策略的研究，Armstrong^[6]指出歧视性定价不仅减弱了竞争对手对自身利润的影响而且也减小了企业与消费者的信息不对称，有利于提升企业利润；Sundararajan分析了消费者需求差异下的定价问题，研究表明歧视定价提高了垄断企业的利润^[7]；Anderson等^[8]考虑了消费者支付意愿，通过构建垄断企业的歧视定价模型，研究了价格歧视使企业获利条件。但斌等^[9]通过细分消费者偏好研究了企业产品的歧视定价策略，发现与单一定价策略相比歧视定价策略获利更高。周慧妮等^[10]认为在竞争市场中非歧视价格策略定价总是高于歧视价格策略，而歧视定价的利润总是高于非歧视定价；Li等^[11]研究指出与没有价格歧视的模型相比，在价格歧视模型下企业获得了更多利润，对环境造成的影响更小；Bergemann等^[12]比较分析了三级价格歧视和统一定价的问题。二是关于大数据下歧视性定价策略的研究，学者们研究指出，在大数据时代企业根据消费者信息实施歧视定价的方法已经不断丰富，如对消费者购买记录进行跟踪^[13-14]、为消费者提供预售折扣作为价格歧视机制^[15]、基于行为的价格歧视的盈利能力^[16]及数据对不同规模的平台企业定价及收益影响^[17-18]等。由于细分市场是实施价格歧视的前提，学术界也开始关注消费者的偏好问题^[19-20]。最近，李世杰^[21]探讨了互联网平台阶梯式定价策略及其产业实践对平台用户规模的影响机理，并指出阶梯式定价机制与价格歧视理论的本质差异。

综上，现有研究主要探讨了同一性定价策略和歧视定价策略的选择问题，学者们对同一性定价还是歧视定价对企业更优产生分歧，但大多数学者都倾向于认为歧视定价对企业更优。然而，没有重视个人信息保护力度、信息搜集成本、定制成本、企业间的技术差距等因素对企业价格决策的影响。为此，本文在大数据背景下建立制造商定价策略的双群体演化博弈模型，研究了个人信息保护力度、信息搜集成本、定制成本、制造商间的技术差距等因素对同一性定价和歧视性定价策略的影响。本文创新之处在于通过构建双群体演化博弈模型揭示制造商群体定价策略的动态演化过程，解析个人信息保护力度、信息搜集成本、定制成本、制造商间的技术差距等因素对制造商定价策略的影响机理。

基于Hotelling线性市场模型，假设市场中存在两类基于iOS平台和Andriod平台的制造商群体，前者如IPHONE、IPAD等，后者如华为、OPPO、VIVO、小米等，两类群体中随机选择位于线性市场[0, 1]两端0和1处的两个代表性制造商0和1，两个制造商为均匀地分布在线性市场中总量为1的消费者提供产品。假设消费者对产品水平偏好类型x(简称“偏好类型”)以其在市场中所处位置表示，每位消费者对该产品愿意支付的保留价格为v^①；据Ishibashi等^[22]的研究，假设偏好类型为x的消费者，在观测到产品价格P(x)和质量水平q后，选择购买一单位或不购买该产品。若购买，则获得效用u(x)=v+q－P(x)，若不购买则效用为0。考虑到IPHONE等产品定位和实际售价，一般而言，基于iOS平台的消费者保留价格高于Andriod，但由于基于Android平台的制造商也逐渐推出高端产品，加之消费者需求的差异性，两个平台的消费者保留价格关系比较复杂，不失一般性，假设基于两个平台的消费者保留价格均为v(v足够大)，故其一定选择购买产品。假设消费者选择购买使自身效用更大的产品或同自身偏好类型更接近的产品，假设消费者产品购买选择与产品质量和价格之差q_i－P_i(x)相关，根据王世强等^[2]的研究称之为产品性价比。

① 当消费者最高支付意愿是可变函数v(x)时，不会改变研究结论^[2]。

对于线性市场两家制造商i(i=0，1)而言，可能产生三类成本，第一类是质量成本，即产品质量水平为q_i，根据Banker等^[23]的研究，每件产品质量成本为c(q_i)=q_i²/2k_i，k_i为可变质量成本系数，越大表示效率越高，相应制造商技术水平越高，且k_i是共同知识；第二类是定制成本，是指制造商投入与消费者偏好相关的成本，以满足消费者特定偏好，对于偏好类型为x的消费者，制造商0的该项成本为tx，制造商1则为t(1－x)，t为单位定制成本。假设市场中消费者偏好分布是共同知识，而每个消费者偏好是私人信息，当制造商无法掌握每个消费者偏好的私人信息时，只能基于消费者偏好分布提供产品并由消费者自行选择购买，此时，制造商只能基于消费者偏好分布进行同一性定价(U)，即产品的价格对任意消费者偏好x均为常数，以制造商1为例，有P₁(x)=p₁+t(1－x)，其中p₁为常数。

三是信息搜寻成本，制造商可运用大数据技术对消费者信息进行分析进而精准识别每个消费者的偏好类型和支付意愿。为获取此类信息，制造商需要付出信息搜寻成本，与制造商自身定位同消费者偏好间的差距相关。例如，偏好iOS平台这类消费者更易在该平台留下搜索痕迹和(或)购买记录，这利于iOS平台对相关消费者进行精准识别，而竞争对手Andriod平台对该类消费者进行精准识别所付出的成本相对较高。假设对偏好类型为x的消费者，制造商0所需付出的信息搜集成本为c₀(x)=cx，制造商1所需付出成本相应为c₁(x)=c(1－x)，c为制造商的单位信息搜寻成本。制造商获取消费者偏好信息后能够将具有某特征的产品直接卖给特定消费者，并采用歧视性定价(D)，即产品价格仍随消费者偏好x的变化而发生改变，以制造商1为例，即P₁(x)=p₁(x)+t(1－x)，其中p₁(x)为与消费者偏好类型x相关的函数。根据Wattal等^[24]的研究，消费者对产品水平特征的偏好使得制造商能够通过满足消费者的偏好来弥补其产品在质量层面的不足，从而仍可制定较高的产品价格，这为制造商选择歧视性定价提供了激励。

进一步假设制造商在线性市场分界点为x₀∈[0, 1]，制造商0市场范围为[0，x₀]，制造商1市场范围为[x₀，1]。制造商搜寻消费者信息产生的总成本为C_i(x₀)，i=0，1。制造商的利润函数分别为$\left.\Pi_0=\int_0^{x_0}\left[P_0(x)-c\left(q_0\right)-t x\right)\right] d x-C_0(x) $和$\Pi_1=\int_{x_0}^1\left[P_1(x)-c\left(q_1\right)-t(1-x)\right] d x-C_1(x) $。当制造商进行歧视性定价时，制造商搜寻消费者信息产生的总成本分别为$C_0(x)=\int_0^{x_0} \alpha c_0(x) d x $和$C_1(x)=\int_{x_0}^1 \alpha c_1(x) d x $，其中α为个人信息保护力度；若制造商进行同一性定价时，不需要支付信息搜寻成本，则c=0，相应的C_i(x)=0，i=0，1。为保证分析在经济学上有意义，参考王世强等^[2]的研究，假设制造商0在质量提升方面具有技术优势即k₀>k₁；为保证技术劣势制造商1不会被逐出市场，假设0＜k₀－k₁＜2t。

本文的博弈结构为，两家制造商同时决定自身质量水平(q₀，q₁)，观测到自身及竞争对手的质量之后，两家制造商决定价格策略U或D，有均选择同一性价格(U，U)，或均选择歧视性价格(D，D)，或只有一家选择歧视性价格(U，D)或(D，U)等四种策略组合，制造商双方的策略选择行为会随时间进行演进，依据制造商群体的平均收益值而做出动态调整。

来自基于iOS平台和基于Andriod平台随机配对的制造商0和制造商1都选择U策略，此时不产生信息搜寻成本，即有C₁(x)=C₂(x)=0。两家制造商价格分别为P₀(x)=p₀+tx和P₁(x)=p₁+t(1－x)。由此易知，市场分界点x₀由两家制造商的价格和质量决定，而在x₀的消费者选择任一家制造商产品获得的效用无差异，即v+q₀－P₀(x)=v+q₁－P₁(x)，解得$x_0= \frac{\left(q_0-p_0-q_1+p_1+t\right)}{2 t} $，进一步代入制造商0和1的利润函数后对p₀和p₁求导，可得两家制造商的优定价，代入制造商0和1的利润后的两家制造商最优利润，进而对q₀和q₁求导可得两家制造商的最优产品质量水平为$q_0^{U{U *}}=k_0, q_1^{U U *}=k_1 $；制造商0和1的最优定价、市场临界点为$p_0^{U U *}=\frac{4 k_0-k_1+6 t}{6}, p_1^{U U *}=\frac{4 k_1-k_0+6 t}{6}, x_0^{U U *}=\frac{k_0-k_1+6 t}{12 t} $；进而可得两家制造商的最优利润分别为$\Pi_0^{U U *}=\frac{\left(k_0-k_1+6 t\right)^2}{72 t}, \Pi_1^{U U *}=\frac{\left(k_0-k_1-6 t\right)^2}{72 t} $。

若制造商0选择U策略，制造商1选择D策略，此时，制造商0采用同一性定价，不产生信息搜集成本，即有C₀(x)=0，其价格表示为P₀(x)=p₀+tx。制造商1基于大数据技术对消费者信息进行搜集，产生信息搜寻成本C₁(x)>0，根据消费者偏好类型x设置产品价格P₁(x)。对偏好类型为x的消费者，若q₁－P₁(x)＜q₀－P₀(x)，制造商1将失去此类消费者；若P₁(x)＜P₀(x)－q₀+q₁，制造商1稍提高自身价格即可获得更高的利润水平。可知，制造商1的定价策略将始终保证其与制造商0的产品性价比相同，满足P₁(x)=P₀(x)－q₀+q₁，此时制造商1的产品价格和市场份额与信息搜寻成本有关。事实上，制造商1为实现利润最大化，在销售范围内每一类消费者的获利均不小于0。故对偏好类型为x的消费者，制造商1的最低定价是$k_1 q_1+\frac{1}{2} q_1^2+t(1-x)+c(1-x) $。故此时市场分界点将满足$p_0+t x-q_0+q_1=\frac{q_1^2}{2 k_1}+t(1-x)+c(1-x) $，类似地易得制造商最优产品质量水平$q_0^{U D *}=k_0, q_1^{U D *}=k_1 $；制造商0和1的最优定价、市场临界点为$p_0^{U D *}=\frac{3 k_0-k_1+2 t+2 c}{4}, p_1^{U D *}=\frac{(4 t+3 c) k_1-c k_0+2 c(3 t+c)}{4(2 t+c)}, x_0^{U D *}=\frac{\left(k_0-k_1+2 t+2 c\right)}{4(2 t+c)} $；制造商的最优利润分别为$\Pi_0^{U D *}=\frac{\left(k_0-k_1+2(t+c)\right)^2}{16(2 t+c)}, \Pi_1^{U D *}=\frac{(2 t+2 c-c \alpha)\left(k_0-k_1-2(3 t+c)\right)^2}{32(2 t+c)^2} $。

若制造商0选择D策略，制造商1选择U策略，此时，制造商1采用同一性定价，不产生信息搜集成本，即有C₁(x)=0，其价格表示为P₁(x)=p₁+t(1－x)。制造商0基于大数据技术对消费者信息进行搜集，产生信息搜寻成本C₀(x)>0，并进行价格歧视，根据消费者偏好类型x设置产品价格P₀(x)。对偏好类型为x的消费者，若q₀－P₀(x)＜q₁－P₁(x)，制造商0将失去此类消费者；若P₀(x)＜P₁(x)－q₁+q₀，制造商0稍提高自身价格即可获得更高的利润水平。由此可知，制造商0的定价策略将始终保证其与制造商1的产品性价比相同，价格满足P₀(x)=P₁(x)－q₁+q₀，此时制造商0产品价格和市场份额与信息搜寻成本有关。制造商0为实现利润最大化，在销售范围内每一类消费者处获得的利润均不小于0。故对偏好类型为x的消费者，制造商0的最低定价是自身成本$\frac{q_0^2}{2 k_0}+t x+c x$。故此时市场分界点满足$p_1+t(1-x)-q_1+q_0=\frac{q_0^2}{2 k_0}+t x+c x$，类似地易得制造商最优产品质量水平$q_0^{D U *}=k_0, q_1^{D U *}=k_1$；制造商0和1的最优定价、市场临界点为$p_0^{D U *}=\frac{(4 t+3 c) k_0-c k_1+2 c(3 t+c)}{4(2 t+c)}, p_1^{D U *}=\frac{3 k_1-k_0+2 t+2 c}{4}, x_0^{D U *}=\frac{k_0-k_1+6 t+2 c}{4(2 t+c)}$；制造商的最优利润分别为$\Pi_0^{D U *}=\frac{(2 t+2 c-c \alpha)\left(k_0-k_1+2(3 t+c)\right)^2}{32(2 t+c)^2}, \Pi_1^{D U *}=$ $\frac{\left(k_0-k_1-2(t+c)\right)^2}{16(2 t+c)}$。

若制造商0和制造商1都选择D策略，此时，两家制造商均进行信息搜寻并选择歧视性定价，双方都会产生信息搜寻成本，有C₀(x)>0及C₁(x)>0，此时两家制造商将根据竞争对手的成本函数确定自身的价格。实际上，对制造商0而言，其对偏好类型为x的消费者所能制定的价格上限P₀(x)满足$\bar{P}_0(x)-q_0=\frac{q_1^2}{2 k_1}+t(1-x)+c(1-x)-q_1$，即保证竞争对手采用成本定价时，自身市场范围内的消费者选择两类产品可取得相同的效用水平。类似地，制造商1所能制定的价格上限P₁(x)满足$\bar{P}_1(x)-q_1=\frac{q_0^2}{2 k_0}+t x+c x-q_0$，此时，两家制造商的市场分界点满足$\frac{q_0^2}{2 k_0}+t x+c x-q_0=\frac{q_1^2}{2 k_1}+t(1-x)+c(1-x)-q_1$，类似地易得制造商最优产品质量水平$q_0^{D D *}=k_0, q_1^{D D *}=k_1$；制造商0和1的最优定价、市场临界点为$p_0^{D D *}=\frac{(2 t+3 c) k_0-c k_1+2 c(t+c)}{4(t+c)}, p_1^{D D *}=\frac{(2 t+3 c) k_1-c k_0+2 c(t+c)}{4(t+c)}, x_0^{D D *}=\frac{k_0-k_1+2 t+2 c}{4(t+c)}$；制造商的最优利润分别为$\Pi_0^{D D *}=\frac{(2 t+3 c-c \alpha)\left(k_0-k_1+2(t+c)\right)^2}{32(t+c)^2}, \Pi_1^{D D *}=\frac{(2 t+3 c-c \alpha)\left(k_0-k_1-2(t+c)\right)^2}{32(t+c)^2}$。综上可得，两家制造商0和1的博弈支付矩阵，如表 1所示：

根据前文分析研究，由表 1可得命题1：

命题1：(1)当制造商1选择策略U时，制造商0选择策略U和D的利润分别为Π₀^UU*和Π₀^DU*，制造商0选择U和D策略的临界点为α₁>0，当α>α₁时，Π₀^UU*－Π₀^DU*>0，制造商0选择U策略；当α＜α₁时，Π₀^UU*－Π₀^DU*＜0，制造商0选择D策略。

(2) 当制造商1选择策略D时，制造商0选择策略U和D的利润分别为Π₀^UD*和Π₀^DD*，制造商0选择U和D策略的临界点为α₂>0，当α>α₂时，Π₀^DD*－Π₀^UD*＜0，制造商0选择U策略；当α＜α₂时，Π₀^DD*－Π₀^UD*>0，制造商0选择D策略。

(3) 当制造商0选择策略U时，制造商1选择策略U和D的利润分别为Π₁^UU*和Π₁^UD*，制造商0选择U和D策略的临界点为α₃>0，当α>α₃时，Π₁^UU*－Π₁^UD*>0，制造商1选择U策略；当α＜α₃时，Π₁^UU*－Π₁^UD*＜0，制造商1选择D策略。

(4) 当制造商0选择策略D时，制造商1选择策略U和D的利润分别为Π₁^DU*和Π₁^DD*，制造商0选择U和D策略的临界点为α₂>0，当α>α₂时，Π₁^DD*－Π₁^DU*＜0，制造商1选择U策略；当α＜α₂时，Π₁^DD*－Π₁^DU*>0，制造商1选择D策略。其中：

命题1表明，当制造商0或1选定策略时，制造商1或0的最优策略与个人信息保护力度有关，且存在一个临界值，当个人信息保护力度α高于该临界值时，此时制造商难以搜集到消费者私人信息进行歧视性定价，制造商将选择同一性定价策略；反之，当个人信息保护力度较低时，制造商将选择歧视性定价策略。

假设制造商0群体中选择U策略的比例为x₀，选择D策略的比例为1－x₀；制造商1群体中选择U策略的比例为x₁，选择D策略的比例为1－x₁。根据复制者动态方程，制造商0选择策略U的数量增长率为$$可表示为$\frac{\dot x_0}{x_0}$减去其平均适应度(x₀，1－x₀)·A(x₁，1－x₁)^T，其中e=(1，0)表示制造商0以1的概率选择U策略，A表示制造商0的支付矩阵，其中$A=\left[\begin{array}{ll} \Pi_0^{U U *} & \Pi_0^{U D *} \\ \Pi_0^{D U *} & \Pi_0^{D D *} \end{array}\right]$。据此，制造商0的复制者动态方程可表示为：

将制造商0的支付矩阵代入复制动态方程(系统)，整理得：

同理，制造商1选择U策略的增长率为$\frac{\dot x_1}{x_1}$可表示为$\left.\left(1-x_1, x_1-1\right)\right) B\left(x_0, 1-x_0\right)^{\mathrm{T}}$，制造商的支付矩阵$B=\left[\begin{array}{ll}\Pi_1^{U U *} & \Pi_1^{D U *} \\ \Pi_1^{U D *} & \Pi_1^{D D *}\end{array}\right]$，整理得制造商1的复制动态方程(系统)为：

根据假设条件及命题1容易判断α₁＜α₃，可得命题2。

命题2根据式(2)和(3)给出的复制动态方程，可得：(1)点(0，0)，(0，1)，(1，0)，(1，1)是复制动态系统的四个均衡点；(2)当个人信息保护力度满足α₁＜α₃＜α＜α₂或α₂＜α＜α₁＜α₃时，(x₀^*，x₁^*)是动态系统的混合均衡点。其中：

根据命题1~2可得命题3，并得出相应的演化稳定策略(ESS)。

命题3当满足0＜k₀－k₁＜2t时，若α₁＜α₃＜α₂，(1)当α＜α₃时，ESS为(D，D)记为(0，0)；(2)当α₃＜α＜α₂时，ESS为(U，U)，(D，D)记为(1，1)，(0，0)；(3)当α>α₂时，ESS为(U，U)记为(1，1)。若α₁＜α₂＜α₃，(1)当α＜α₂时，ESS为(D，D)记为(0，0)；(2)当α₂＜α＜α₃时，ESS为(U，D)记为(1，0)；(3)当α>α₃时，ESS为(U，U)记为(1，1)。若α₂＜α₁＜α₃，(1)当α＜α₂时，ESS为(D，D)记为(0，0)；(2)当α₂＜α＜α₁时，ESS为(U，D)，(D，U)记为(1，0)，(0，1)；(3)当α₁＜α＜α₃时，ESS为(U，D)记为(1，0)；(4)当α>α₃时，ESS为(U，U)记为(1，1)。

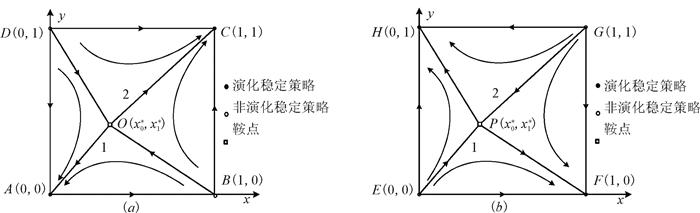
由命题3，只要个人信息保护力度足够大，制造商更倾向于选择U策略即同一性定价策略；当个人信息保护力度较小时，制造商更倾向于选择D策略即歧视性定价策略；当个人信息保护力度适中时，制造商定价策略行为演化与信息搜集成本、定制成本及制造商之间的技术水平差距相关。进而可得稳定点为(1，1)，(0，0)，鞍点为(x₀^*，x₁^*)的相位图如图 1(a)所示，稳定点为(1，0)和(0，1)，鞍点为(x₀^*，x₁^*)的相位图如图 1(b)所示。

根据Weibull^[25]的研究，非对称情况下混合均衡不是ESS，但混合均衡点x₀^*，x₁^*的大小会影响系统演化趋势，根据(x₀^*，x₁^*)可得命题4(相关证明过程如有需要请与作者联系)。

命题4当α₁＜α₃＜α＜α₂时，有$\frac{\partial x_0^*}{\partial \alpha}<0, \frac{\partial x_1^*}{\partial \alpha}<0$；当α₃＜α＜α₄＜α₂或α₄>α₂时，有$\frac{\partial x_0^*}{\partial\left(k_0-k_1\right)}>0$；当α₃＜α₄＜α＜α₂时，有$\frac{\partial x_0^*}{\partial\left(k_0-k_1\right)}<0$；当α₃＜α＜α₅或α₅>α₂时，$\frac{\partial x_1^*}{\partial\left(k_0-k_1\right)}<0$；当α₅＜α₃＜α＜α₂或α₃＜α₅＜α＜α₂时，$\frac{\partial x_1^*}{\partial\left(k_0-k_1\right)}>0$；当α₂＜α＜α₁＜α₃时，有$\frac{\partial x_0^*}{\partial \alpha}>0, \frac{\partial x_1^*}{\partial \alpha}>0, \frac{\partial x_0^*}{\partial\left(k_0-k_1\right)}<0, \frac{\partial x_1^*}{\partial\left(k_0-k_1\right)}>0$。其中，$\alpha_4= \frac{\left(18 t^2(t+c)\left(k_0-k_1-6 t-2 c\right)-2(2 t+c)^2(2 t-c)\left(k_0-k_1-6 t\right)\right)}{9 t^2 c\left(k_0-k_1-6 t-2 c\right)} $；$\alpha_5=\frac{\left(18 t^2(t+c)\left(k_0-k_1+6 t+2 c\right)-2(2 t+c)^2(2 t-c)\left(k_0-k_1+6 t\right)\right)}{9 t^2 c\left(k_0-k_1+6 t+2 c\right)}$。

由命题4，个人信息保护力度α及两家制造商可变成本质量成本系数之差(k₀－k₁)通过影响(0，0)、(1，1)的吸引域进而对系统演化产生影响。当α₁＜α₃＜α＜α₂时，x₀^*和x₁^*都是α的严格减函数，此时随α增加，均衡点(1，1)的吸引域增大，系统的ESS演化至(1，1)的概率变大，反之演化稳定至(0，0)的概率增大；当α₃＜α＜α₄＜α₂或α₄>α₂时，x₀^*是(k₀－k₁)的严格增函数；当α₅＜α₃＜α＜α₂或α₃＜α₅＜α＜α₂时，x₁^*是(k₀－k₁)的严格递增函数，此时随着(k₀－k₁)的增加，系统的ESS演化至(0，0)的概率增大，反之系统演化稳定至(1，1)的概率变大；当α₃＜α₄＜α＜α₂时，x₀^*是(k₀－k₁)的严格减函数，当α₃＜α＜α₅或α₅>α₂时，x₁^*是(k₀－k₁)的严格递减函数，此时随着(k₀－k₁)的增加，系统的ESS演化至(1，1)的概率增大，反之演化稳定至(0，0)的概率变大；当α₂＜α＜α₁＜α₃时，x₀^*和x₁^*都是α的严格增函数；x₀^*是(k₀－k₁)的严格减函数，x₁^*是(k₀－k₁)的严格增函数，即随着α的增加均衡点(0，0)的吸引域增大，系统的ESS演化至(0，0)的概率变大，反之演化稳定至(1，1)的概率变大，此时(k₀－k₁)的影响取决于x₀^*和x₁^*的相对增减幅度。当混合均衡点存在时，还受单位信息搜寻成本、单位定制成本等的影响，由于影响较复杂，下面通过数值分析进行解析。

本节通过数值分析对相关命题及结论进行验证。根据复制动态方程(2)和(3)，对$\dot{x}_0$和$\dot{x}_1$分别关于$\dot{x}_0$和$\dot{x}_1$求偏导数，可得雅可比矩阵$J=\left[\begin{array}{l}\partial \dot{x}_0 / \partial x_0 \partial \dot{x}_0 / \partial x_1 \\ \partial \dot{x}_1 / \partial x_0 \partial \dot{x}_1 / \partial x_1\end{array}\right]$，据此判断复制动态系统的均衡点(0，0)，(0，1)，(1，0)，(1，1)和(x₀^*，x₁^*)的局部稳定性，即当detJ>0且σ_o^F＜σ_m^F时，均衡点为ESS，当detJ＜0时，为鞍点，否则为不稳定点。

设k₀=1，k₁=0.5，c=1，t=1(满足条件0＜k₀－k₁＜2t，下同)，由命题1可得3个临界值点分别为α₁=1.660 9，α₂=2.333 3，α₃=1.848 9，个人信息保护力度取值α=1，α=2，α=3，运用Mathematica软件计算结果如表 2所示。设k₀=1，k₁=0.1，c=1，t=0.6，根据命题1可得3个临界值点为α₁=1.481 7，α₂=1.872 7，α₃=2.016 8，个人信息保护力度取值α=1，α=2，α=3，如表 3所示。设k₀=0.3，k₁=0.1，c=1，t=0.2，根据命题1可得3个临界值点分别为α₁=1.661 5，α₂=1.342 9，α₃=1.916 1，个人信息保护力度分别取值α=1.2，α=1.5，α=1.8，α=2.1，如表 4所示。

由表 2~4易得相关算例结果与命题3一致，当α₁＜α₃＜α₂时，若个人信息保护力度α=1，平衡点(0，0)是系统的ESS，制造商0和1均选择歧视性定价策略；若α=2，(0，0)和(1，1)是系统的ESS，制造商0和1均选择同一性定价策略或均选择歧视性定价策略；若α=3，点(1，1)是系统的ESS，制造商0和1均选择同一性定价策略。当α₁＜α₂＜α₃时，若α=1，点(0，0)是系统的ESS，制造商0和1均选择歧视性定价策略；若α=2，点(1，0)是系统的ESS，制造商0选择同一性定价策略而制造商1选择歧视性定价策略；若α=3，(1，1)是系统的ESS，制造商0和1均选择同一性定价策略。当α₂＜α₁＜α₃时，若α=1.2，(0，0)是系统的ESS，制造商0和1均选择歧视性定价策略；若α=1.5，(0，1)和(1，0)是系统的ESS，制造商0和1选择相反策略；若α=1.8，(1，0)是系统的ESS，制造商0选择同一性定价策略而制造商1选择歧视性定价策略；若α=2.1，(1，1)是系统的ESS，制造商0和1均选择同一性定价策略。

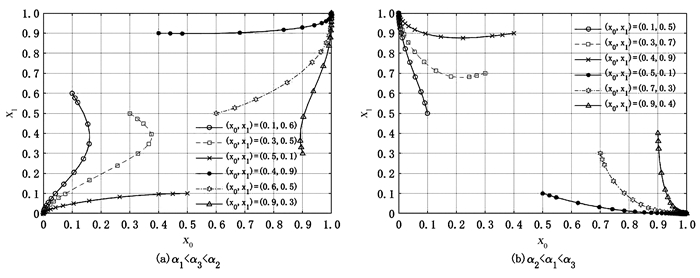
当α₁＜α₃＜α₂时，设k₀=1，k₁=0.5，c=1，t=1，α=2(若没有特别说明，下文参数取值与此保持一致)，(x₀，x₁)分别取值(0.1，0.6)，(0.3，0.5)，(0.5，0.1)，(0.4，0.9)，(0.6，0.5)，(0.9，0.3)，如图 2(a)所示。当α₂＜α₁＜α₃时，设k₀=0.3，k₁=0.1，c=1，t=0.2，α=1.5(若没有特别说明，下文参数取值与此保持一致)，(x₀，x₁)分别取值(0.1，0.5)，(0.3，0.7)，(0.4，0.9)，(0.5，0.1)，(0.7，0.3)，(0.9，0.4)，如图 2(b)所示。

由图 2(a)可知，当(x₀，x₁)取不同的初始值，系统演化结果将收敛于不同的点，在初始值设定状态下，鞍点的值为(0.5194，0.3827)，结合图 1可知，当(x₀，x₁)初始值落在ABOD区域时，系统演化稳定于均衡(0，0)，博弈主体将选择歧视性定价策略。当(x₀，x₁)初始值落在BCDO区域时，系统演化稳定于均衡(1，1)，博弈主体将选择同一性定价策略。由图 2(b)可知，在初始值设定状态下，鞍点的值为(0.2166，0.4364)，当(x₀，x₁)初始值落在EPGH区域时，博弈系统稳定于均衡(0，1)，制造商0将选择歧视性定价策略而制造商1将选择同一性定价策略。当(x₀，x₁)初始值落在EFGP区域时，系统演化稳定于均衡点(1，0)，制造商0将选择同一性定价策略而制造商1将选择歧视性定价策略。可知，双方策略演化结果对初始值具有依赖性，根据命题4，不同参数对博弈主体演化结果有一定影响，下面将分析α、k₀－k₁、c、t等参数对博弈系统演化的影响。

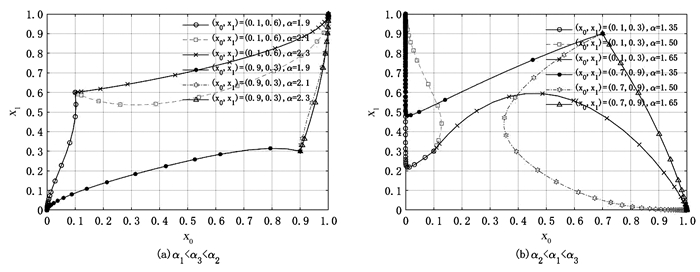
个人信息保护力度α的影响如图 3所示，其余参数保持不变，当α₁＜α₃＜α₂时，α分别取值1.9，2.1，2.3，以(0.1，0.6)和(0.9，0.3)为基准进行分析，如图 3(a)所示，随着α增大，ESS由(0，0)变为(1，1)，制造商0和1均倾向于选择同一性定价策略。当α₂＜α₁＜α₃时，α分别取值1.35，1.50，1.65，以(0.1，0.3)和(0.7，0.9)为基准进行分析，如图 3(b)所示，随着α增大，ESS由(0，1)变为(1，0)，制造商0倾向于选择同一性定价策略而制造商1倾向于选择歧视性定价策略。

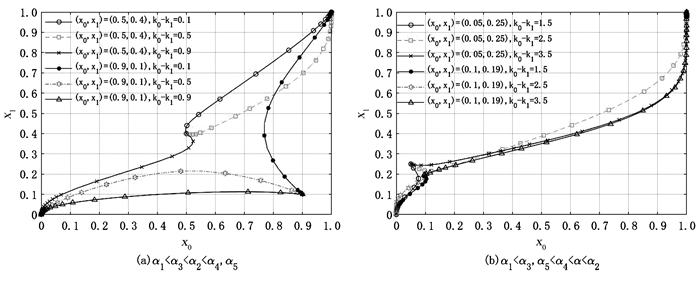
制造商技术差距k₀－k₁对混合均衡的影响如图 4所示，其余参数保持不变，当α₁＜α₃＜α₂时，若满足α₄>α₂，α₅>α₂，k₀分别取值0.6，1.0，1.4，即k₀－k₁为0.1，0.5，0.9，以(0.5，0.4)，(0.9，0.1)为基准进行分析，如图 4(a)所示，随着k₀－k₁增加，ESS由(1，1)变为(0，0)，制造商0和1均倾向于选择歧视性定价策略。若满足α₃＜α₄＜α＜α₂，α₅＜α₃＜α＜α₂或α₃＜α₅＜α＜α₂，则取值α=3，t=2，k₀分别取值2，3，4，即k₀－k₁为1.5，2.5，3.5，以(0.05，0.25)，(0.1，0.19)为基准进行分析，如图 4(b)所示，随着k₀－k₁增加，ESS由(0，0)变为(1，1)，制造商0和1均倾向于选择同一性定价策略。在特定条件下，若α₃＜α＜α₄＜α₂，α₃＜α＜α₅，随k₀－k₁增加制造商0和1均倾向于选择歧视性定价策略，当α₂＜α₁＜α₃时，随k₀－k₁增加，制造商0选择同一性定价策略而制造商1倾向于歧视性定价策略，这与图 4分析类似，不再赘述。

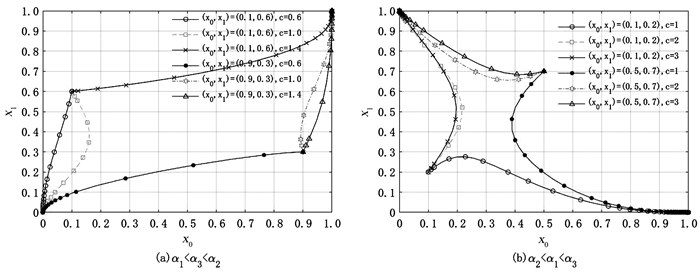
如图 5所示，当α₁＜α₃＜α₂时，c分别取值0.6，1.0，1.4，其余参数保持不变，以(0.1，0.6)，(0.9，0.3)为基准进行分析，如图 5(a)所示，随着c增加，ESS由(0，0)变为(1，1)，制造商0和1均倾向于选择同一性定价策略。当α₂＜α₁＜α₃时，c分别取值1，2，3，以(0.1，0.2)，(0.5，0.7)为基准进行分析，如图 5(b)所示，随着c增加，ESS由(1，0)变为(0，1)，制造商0倾向于选择歧视性定价策略而制造商1倾向于选择同一性定价策略。单位定制成本的影响与图 5类似，在特定条件下，当α₁＜α₃＜α₂时，随着t增加，制造商0和1均倾向于选择歧视性定价策略，当α₂＜α₁＜α₃时，随着t增加，制造商0倾向于选择歧视性定价策略而制造商1倾向于选择同一性定价策略，在此不再赘述。

本文在大数据背景下构建了制造商定价策略的双群体演化博弈模型，解析了制造商面对同一性价格和歧视性价格策略的演化稳定策略及影响因素。研究发现，给定对方制造商的定价策略，制造商的最优策略与个人信息保护力度大小有关，且存在一个临界值，当个人信息保护力度高于该临界值时，制造商选择同一性定价策略；反之选择歧视性定价策略；当个人信息保护力度适中时，制造商定价策略行为演化与信息搜集成本、定制成本及制造商之间的技术水平差距相关。个人信息保护力度及两家制造商可变成本质量成本系数之差通过影响演化稳定策略(同一性定价，同一性定价)和(歧视性定价，歧视性定价)的吸引域对制造商定价策略系统演化产生影响，当混合均衡点存在时，系统演化的影响受到单位信息搜寻成本、单位定制成本等的影响，具体影响机理需要做具体分析。

根据上述研究结论，个人信息保护力度对于制造商选择同一性定价还是歧视性定价策略有重要影响。如何采取符合市场规律的消费者个人信息保护策略，以规避消费者对网络交易市场信任的下降，不仅需要国家出台相关法律法规并严格执行，如2021年实施的《中华人民共和国个人信息保护法》，为消费者个人信息保护提供根本遵循；同时，需要理解制造商定价策略的演化机理，通过声誉机制、惩罚机制等，具体通过面向大众曝光、具有威慑性的惩罚等举措，对制造商价格歧视行为产生威慑，进而抑制制造商采取歧视性定价策略。还可通过运用相应技术加密、去标识化等措施，规避消费者个人信息遭到泄露、丢失，增加制造商的个人信息获取成本。此外，增强消费者个人的隐私保护意识，提升制造商获取个人信息的成本，也是强化个人信息保护力度的重要方面。

下一步，可引入第三方监管机构，构建其与制造商、消费者的三方演化博弈模型，进而系统地揭示三方博弈的演化稳定策略及企业定价策略的演化动态。还可区分不同的市场产品，解析企业定价策略与消费者类型、产品特性之间的动态匹配机制，这是一个有趣且极具挑战性研究话题，也构成本文的一个拓展性研究方向。