-
自1963年Lorenz[1]提出第一个三维自治混沌系统以来,大量三维混沌系统被构造[2-5],这些系统的研究也激发了人们对Lorenz类系统的探讨.由于平面自治系统不可能产生混沌,而在自治系统中出现混沌至少是三维,因此,在对混沌机理讨论过程中,三维二次自治系统的研究对揭示混沌的产生机理具有特别重要的意义.对于Lorenz类的系统,其混沌判定的定性准则主要是通过Shilnikov定理[6-7]来进行,且要求至少具有一个不稳定的双曲平衡点(鞍焦型),然而Shilnikov定理只是混沌产生的充分条件,而非必要条件,这样对于具有稳定平衡点甚至是没有平衡点或者有无穷多平衡点的系统,在远离平衡点处是否会产生混沌就成为一个新的课题,同时其系统的全局动力学行为等相关问题也会成为数学工作者和工程技术人员面临的一个重要挑战,而且,这些研究无论是对混沌理论或者是混沌应用都至关重要.近几年新的混沌系统不断被提出[5-15],然而这些系统几乎都是通过计算机数值仿真对系统的Lyapunov指数、分岔图、平衡点稳定性等进行分析,其全局动力学行为以及系统的各类分岔行为、周期行为等并没有得到深入的理论分析.为了定性研究此类系统的内部结构以及动力学行为,本文在给出一类具有隐藏吸引子的三维Jerk混沌系统
的基础上,首先通过数值仿真对其基本动力学进行分析,进而运用Poincare紧致化理论对系统(1) 的无穷远动力学进行分析,同时运用平均方法,采用扰动理论对系统(1) 的周期解进行定性分析,并运用数值仿真进行了验证.
全文HTML
-
令
$ \dot{x}=0, \dot{y}=0, \dot{z}=0 $ ,系统(1) 仅有一个平衡点O(0,0,0),且在O处的Jacobian矩阵的特征多项式为f(λ)=λ3+cλ2+bλ+a,根据Routh-Hurwitz准则可知当c>0,a>0且bc-a>0时,特征方程有3个负实部根,因此系统零平衡点为稳定结点或者为稳定结焦点;当c>0,a>0且bc-a<0时,零平衡点为鞍焦点. -
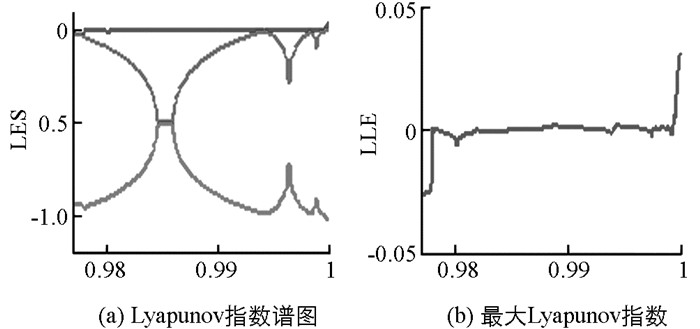
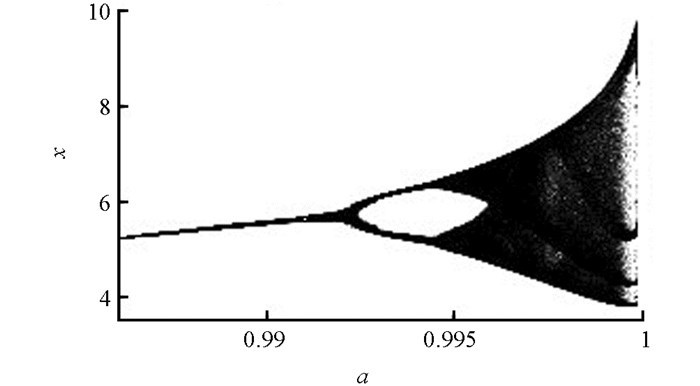
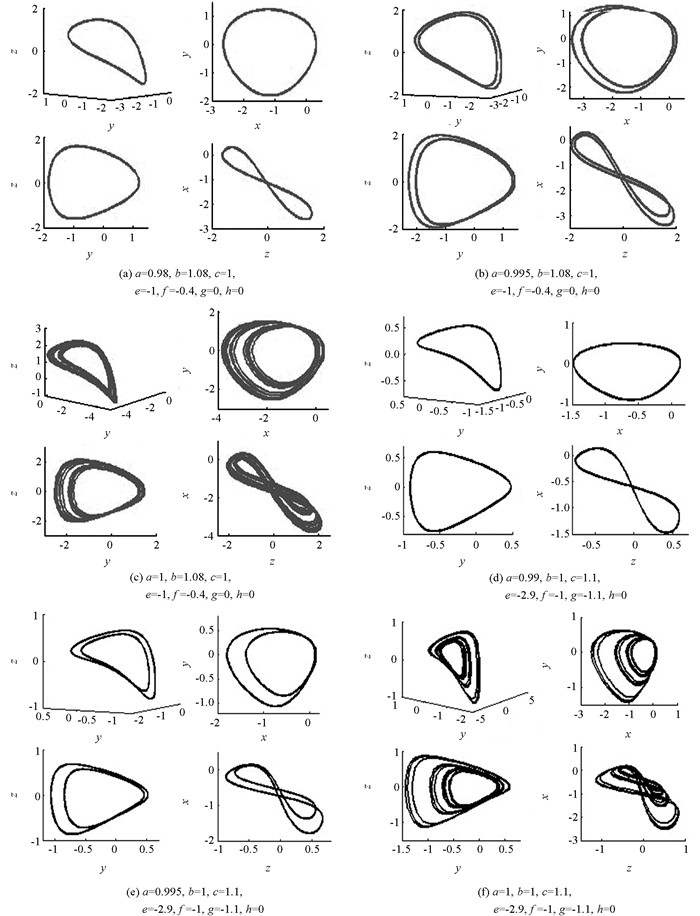
为了能够研究系统(1) 的复杂动力学行为,运用数值方法对系统在不同参数条件下的动力学行为进行了分析(表 1),相应得到了单周期吸引子、双周期吸引子和混沌吸引子(图 1),同时给出了各参数条件下的Lyapunov指数谱图及相应的最大Lyapunov指数图(图 2、图 3).图 4给出了在参数b=0.6,c=2,e=1,f=0.4,g=h=0下,系统(1) 关于参数a的分叉图.
1.1. 平衡点与稳定性
1.2. 混沌与复杂性
-
为了能够了解系统(1) 的全局结构,运用三维空间Poincare紧致化理论[16]来研究系统(1) 的无穷远动力学行为.在
$ {{\mathbb{R}}^{4}} $ 中取单位Poincare球且令
和
分别为北半球和南半球,定义在点(±1,0,0,0),(0,±1,0,0),(0,0,±1,0),(0,0,0,±1) 处的正切超平面为Ui,Vi,其中
为了得到在x,y,z无穷远处的动力学行为,我们仅需要考虑在超平面Ui,Vi(i=1,2,3) 上的动力学即可.
-
令
且t=wτ,则系统(1)变为
如果w=0,则系统(2)化为
可以计算系统(3)过初值(u,v)=(u(0),v(0))的解为
其中
在平面V1上的动力学行为和在U1上的动力学行为相同,方向反向.
-
令
且t=wτ,则系统(1)变为
如果w=0,则系统(3)化为
可以计算系统(5) 过初值(u,v)=(u(0),v(0))的解为
其中
在平面V2上的动力学行为和在U2上的动力学行为相同,方向反向.
-
令
且t=wτ,则系统(1)变为
如果w=0,则系统(6) 化为
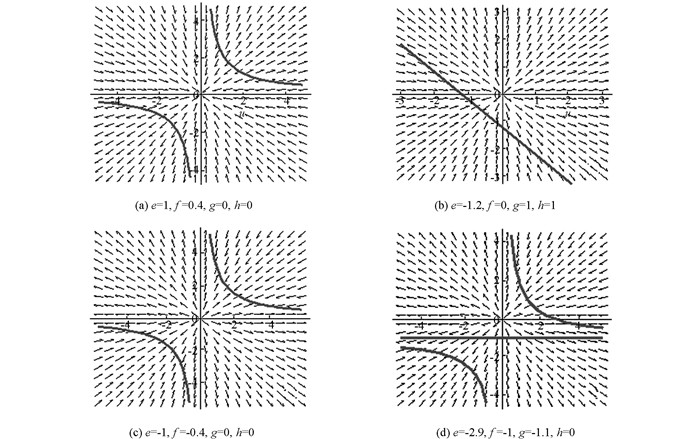
显然,当e>0时,平衡点O(0,0)为稳定结点,当e<0时,O(0,0) 为不稳定结点.同时取不同参数e,f,g,h,运用零倾线分析方法[17],其动力学行为见表 2及图10-13.在平面V3上的动力学行为和在U3上的动力学行为相同,方向反向.
2.1. 超平面U1和V1上的动力学
2.2. 超平面U2和V2上的动力学
2.3. 超平面U3和V3上的动力学
-
从图 3可以看到,当参数a变换时,系统(1) 会产生周期轨道,同时从特征方程可以看到,当参数a=c=0,b>0时,系统会出现零特征及纯虚特征根,即系统(1) 会发生Zero-Hopf分叉,且为了定性分析极限环的出现,本节拟采用平均化方法[18]进行周期轨道分析,并定性分析出周期解的表达式,为此首先介绍等时系统扰动理论[19].
引理1[19] 考虑微分方程
其中:
$ \left( t, \mathit{\boldsymbol{x}}, \varepsilon \right)\in \mathbb{R}\times \mathit{\boldsymbol{ }}\!\!\mathit{Ω}\!\!\rm{ }\times \left( -{{\varepsilon }_{0}}, {{\varepsilon }_{0}} \right)$ ,Ω是$ {{\mathbb{R}}^\mathit{n}} $ 中的一个开集;F0,F1,F2是C2光滑且关于时间t的周期为T的函数.令x(t,z)是(8) 式的解,且当ε=0时,有x(0,z)=z.记Mz(t)是变分方程$ \mathit{\boldsymbol{\dot{y}=}}{{D}_{x}}{{\mathit{\boldsymbol{F}}}_{0}}\left( t, \mathit{\boldsymbol{x}}\left( t, \mathit{\boldsymbol{z}} \right)\right)\mathit{\boldsymbol{y}} $ 的基解矩阵,且Mz(0) 是单位矩阵.假设存在一个有界开子集V及其闭包cl(V)$ \subset $ Ω,对于任意z∈cl(V),解x(t,z)是T周期的.如果a∈V是映射F:cl(V)$ \longrightarrow $ $ {{\mathbb{R}}^\mathit{n}} $ 的简单零点,即F(a)=0,det(DzF(a))≠0,其中则对于充分小|ε|>0,系统(8) 有T周期解
$ \varphi $ (t,ε)满足$ \mathop {\lim }\limits_{\varepsilon \to 0} {\mkern 1mu} \varphi $ (0,ε)=a.定理1 当参数a=c=0,b>0时,系统(1) 在零平衡点处发生Zero-Hopf分叉,且对于充分小的a>0,c>0,系统(1) 分支出的周期解可解析表示为
证 对于任意ε≠0,做变量变换
$ x=\varepsilon \tilde{x}, y=\varepsilon \tilde{y}, z=\varepsilon \sqrt{b}\tilde{z}, a=\varepsilon \tilde{a}, c=\varepsilon \tilde{c} $ ,则系统(1) 可变为令
$ \left( \tilde{x}, \tilde{y}, \tilde{z} \right)\to \left( \tilde{x}, r\sin \theta, r\cos \theta \right)$ ,则系统(9) 可化为其中
进而可以转化为二维系统
其中f1,f2是两个解析函数.
对于任意初值,
$ {{\tilde{x}}_{0}} $ ,r0,系统(11)ε=0有周期为2π的周期解显然系统(11)ε=0沿着解(12) 的变分方程为
时变系统(13)有基解矩阵
根据引理1有
其中
令
有
由于
则由引理1知,对于充分小的|ε|>0,系统(11) 有周期为2π的周期解(
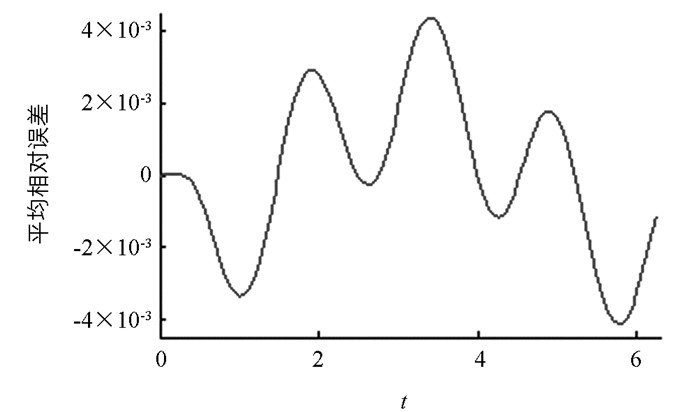
$ \tilde{x} $ (θ),r(θ)),且当ε→0时,故系统(1) 有近似周期解为
证毕.
-
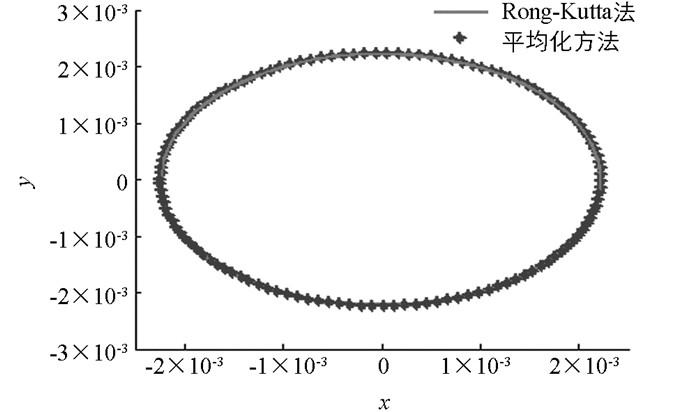
本文首先通过数值理论,计算并分析了一类具有隐藏吸引子的三维Jerk系统的基本动力学行为,包括周期1吸引子,周期2吸引子,混沌吸引子,Lyapunov指数谱和系统关于参数a的分叉等,进而运用三维空间多项式向量场Poincare紧致化理论,定性分析了三维Jerk系统的无穷远点动力学行为,同时为了研究系统在参数a,c扰动下的周期解,运用平均化方法和等时系统扰动理论,定性计算了系统(1) 的周期解,并通过数值仿真进行了实验,验证了理论分析的正确性.根据数值仿真,可以看到运用平均化方法所得解析周期解与Rong-Kutta方法所得数值解基本一致.当然还可以继续分析该系统的分叉动力学行为等,虽然本文也已经提及Zero-Hopf分叉,然限于篇幅,对系统的分叉规范型等的深入讨论此处从略.



 下载:
下载: