-
当汽车行驶时,减振器通过小孔节流将路面激励的振动能量转换为热能耗散掉,满足了车辆的平顺性要求.路况恶劣时,减振器的温度会超过100℃,容易导致其密封件失效,引发减振液的泄漏.同时,系统参数值会发生明显的变化,造成外特性畸变并出现冲击和噪声[1].如果将回收的振动能量转换为电能储存,就可以增加电动汽车的续驶里程.此外,汽车的主动悬架相比半主动悬架、被动悬架的性能优势明显,但高能耗限制了其推广普及,若将振动能量再生,则有助于解决上述问题,因而开展相关的研究势在必行.
国内外关于振动能量的回收已取得了一些进展. 2009年,麻省理工学院设计了图 1所示的回收系统GenShock,其最高可节能10%. 2011年7月,纽约州立大学石溪分校教授左雷等人研制了一款能回收振动能量的系统,结构见图 2所示,研究表明该机构最高可节能8%[2]. David A Crolla等研究了馈能悬架对车辆动力学的影响,回顾了近年来在车辆动力学及控制领域所取得的研究成果[3]. Farbod Khoshnoud等研究了使用再生力作动器回收振动能量,在理论分析的基础上,使用0~20 Hz的道路激励台架进行了试验,仿真结果和试验数据比较接近,充分证明了振动能量回收的可行性[4].
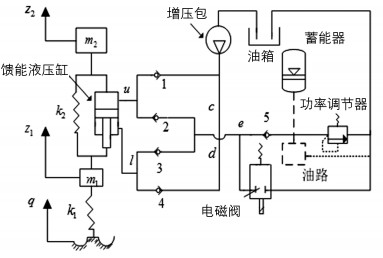
国内关于振动能量回收的研究,有代表性的是上海交通大学和江苏大学的研究成果.上海交通大学的喻凡教授对馈能式主动悬架进行了研究,给出了图 3所示基于直线电机的能量回收系统[5].江苏大学的陈士安等提出如图 4所示的能量回收方案[6].此外,吉林大学、西南交通大学、武汉理工大学及北京理工大学等也在此研究领域取得了重要进展,具体的研究成果参见文献[7-10].
综上所述,能量回收系统可以分为直线电机式、液压式、电磁式、齿轮齿条式等,将振动能量转换为液压能或电能储存,总体看对振动能量回收的研究还比较少,鲜有在实车上成功应用的报道.因此,基于回收机理的研究亟待加强.
全文HTML
-
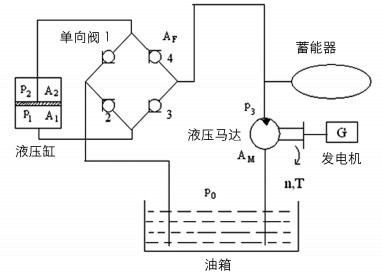
液压式能量回收系统能较好缓冲振动的冲击,有助于实现车辆良好的平顺性.从传统减振器的结构出发,设计出图 5的能量回收方案.能量回收系统由液压缸、单向阀、蓄能器、液压马达、油箱及油管组成.其回收原理为:当活塞杆向上运动,油液获得动能迫使单向阀4开启,然后再通过液压马达到达油箱,液压马达的旋转会带动发电机产生电能,完成振动能量再生.此外,为防止液压马达转速发生波动,在液压回路设有蓄能器,活塞杆向下运动时的工作过程类似.由于采用了4个单向阀,液压马达的转动方向不发生变化.当液压缸中的压强降低时补偿油路能迅速开启,避免液压缸出现真空.
-
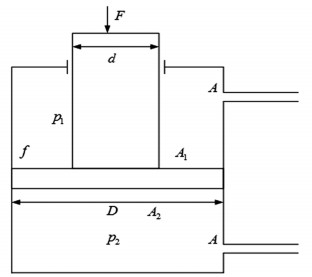
在能量回收系统中,要提高能量回收的效率,还需要对液压缸进行受力分析,以便对系统进行优化分析如图 6所示.设活塞杆的直径为d,受到的作用力为F,上腔的有效面积A1,下腔的有效面积为A2,活塞的直径为D,上腔的压强为p1,下腔压强为p2,单向阀、液压马达和管路的压降分别为pd,pm和pl,
$\dot Z$ 为液流通过油管截面的速度,小孔油管截面的面积为A,ηV、ηM分别为容积效率和机械效率.以活塞为研究对象,当活塞杆向下运动时有其中,
${A_2} = \frac{\pi }{4}{D^2}$ ,f为缸壁的摩擦力,t1为油液完成从液压缸下腔流经截面A的时刻.相似地,可以计算出活塞杆向上运动时回收的液压能
其中,
${A_1} = \frac{\pi }{4}({D^2}-{d^2})$ ,t2为液流完成从上腔流经截面A的时刻.依据公式(1) 和(2),则活塞杆运动一个完整的周期可以回收的能量为
液压马达的转动会驱动发电机产生电流,则一个周期T内生成的电能为
其中,ce、φ、n和i分别为发电机的电磁系数、磁通量、转速和电流.由于系统存在摩擦等能量损耗,公式(3) 的数值必然大于公式(4) 的计算结果.
-
从理论上讲,只要使用传感器等工具测出公式(3) 和公式(4) 的相关变量值的大小,就能够计算出液压缸在一个周期内转换的液压能和电能.由于能量回收系统在工作中变量大小在不停地变化,实现精确计算工作量过于繁重且成本较高,因此,有必要使用专业的软件进行建模分析.
Dshplus软件由德国亚琛工业大学液压与气动研究所IHP研制开发,是一款著名的流体传动与控制系统仿真工具.该软件自带丰富的模型库和数据库,通过搭建直观的图形化液压气动系统原理图,可以方便地对流体控制系统进行各种建模、仿真和分析.同时,该软件还可以与物理硬件连接实现硬件在环实时仿真.
常用减振器的示功图通常是伸张行程的面积大于压缩行程的面积.换言之,即减振器在伸张行程所消耗的振动能量远大于压缩行程消耗的能量.为了简化液压能量回收系统的结构,现只回收伸张行程的振动能量.简化后的回收模型见图 7所示,其振动频率f=0.83 Hz的示功图见图 8.很明显,其形状与传统减振器的结果极为相似.
1.1. 液压缸的受力分析
1.2. 理论建模
-
能量回收系统的目的主要是消除耗能部件的热失效,并将振动激励转换为电能储存用以延长电动车的续驶里程.为验证能量回收系统的性能,需要确定相关的参数进行仿真分析.鉴于道路对于系统的重要作用,有必要简要分析道路的模型.
-
作为车辆振动输入的路面不平度,主要采用路面功率谱密度描述其统计特性.汽车的道路功率谱通常采用下面的拟合公式
式中n为空间频率(m-1),n0为参考空间频率(n0=0.1m-1),Gq(n0)为参考空间频率n0下的功率谱密度值,即路面不平系数. W为频率指数,通常取W=2.
根据f=un,f为时间频率,u为车速,可将空间功率谱密度化为时间功率谱密度
式(6) 表明,时间功率谱密度既与路面不平度系数有关,还与车辆的行驶速度相关[11].
-
将能量回收系统应用于汽车悬架模型中,依据公式(5) 和公式(6) 设置不同等级的路面和车辆速度,得到如下的仿真数据.
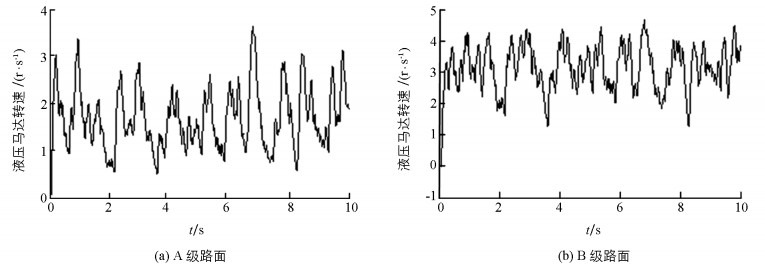
图 9是能量回收系统阻尼力的仿真结果.其中(a)为A级路面、速度为10 m/s时的阻尼力,(b)为B级路面、20 m/s时的阻尼力.很显然,车辆的行驶速度越快、路面越粗糙系统产生的阻尼力就越大. 图 10是能量回收系统中液压马达的转速,与图 9的路面等级及车辆速度相对应. 图 10的数据表明,液压马达的转动方向唯一,转速会发生波动且与路面的粗糙度和车辆的行驶速度相关.
路面越粗糙、行驶速度越高,则汽车行驶时会消耗更多的能量,而车身的振动也更剧烈.鉴于用再生能量的数值难以衡量能量回收系统的性能,因此有必要对其工作效率进行研究.按照减振器的试验规范QC/T491-1999《汽车筒式减振器尺寸系列及技术条件》、QC/T545-1999《汽车筒式减振器台架试验方法》等分别对特定的频率进行分析,具体结果见表 1.
-
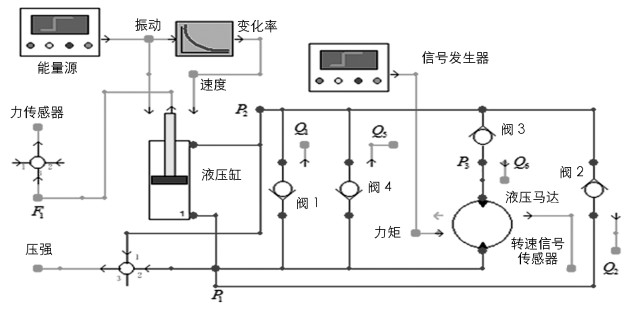
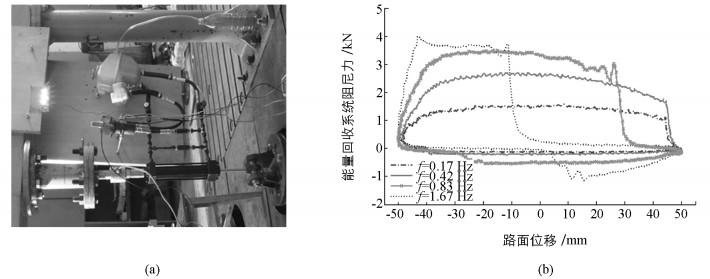
理论模型的仿真数据描述了不同因素对结果的影响,给出了一些工况下的数据.为了增强理论分析的科学性和可靠性,按照图 5的能量回收方案,搭建了图 11(a)的试验台架,图 11(b)是台架在几个特定频率下的试验结果.
图 11(b)的试验结果表明,能量回收系统的示功图与减振器的结果极为相似.随着振动频率的升高,示功图的空程性畸变显著增加.主要原因有两点:① 液流中溶解有空气,液流的压力变化导致气泡析出,使得单向阀不能及时打开;② 系统的补偿油路过长,频率越高则补偿的时间越短暂,液压缸的腔室难以及时补偿.因此,进一步增加系统的集成度是解决其畸变的有效手段.
公式(4) 表明,再生的电能与电机的参数有关,故选取了两个工作电压和转速相异的电机进行试验,结果见表 2.数据表明电机再生的效率为10%左右,这与仿真的结果吻合.仿真结果偏大的原因是将油液当成了理想流体,忽略了部分摩擦力之缘故.如要回收更多的能量,可对公式(4) 所涉及的参数进行改进,必将进一步提升振动能量的回收效率.
2.1. 道路模型的分析
2.2. 振动能量回收系统的仿真
2.3. 振动能量回收系统的试验
-
1) 设计的振动能量回收系统可以避免减振器的热失效,且将振动能量的10%转化为电能.
2) 仿真的结果和试验数据比较吻合,所完成的研究可信度较高.
3) 需要对原理样机进行集成,缩短管路的长度以便于在高频下能可靠地工作,把伸张回路和压缩回路集成在液压缸内部,或许是解决样机现有问题的一个突破口.




 下载:
下载: