-
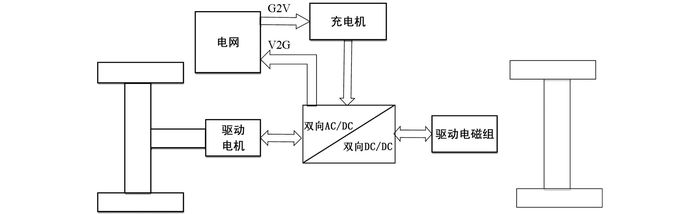
随着经济和科技的飞速发展,人类对能源的需求和要求进一步提高,世界各国都在探寻和研究可再生绿色能源[1].但是如果直接将新能源发出的电量并入电网系统中,会对电网的稳定和电能质量造成影响,无法安全可靠地保证电网的正常运行[2].因此,在电力微网系统中应用了变换技术和电池储能技术来提高电能质量.变换技术中双向DC-DC变换器最为突出,能完成能量的流向控制,因此广泛应用于各领域中[3].以燃料电池电动汽车为例,燃料电池电动车供电系统结构图如图 1所示,燃料电池系统中的用电设备主要为压缩机,电动汽车在平时的行驶过程中,燃料电池向压缩机及汽车内部用电设备提供运行所需的电能,当电动汽车启动时,燃料电池的电压较低,不足以完全支撑电动汽车系统中用电设备的运行,这时双向DC-DC变换器将工作在BOOST升压模式,将蓄电池存储的能量输出至负载端,防止在启动时燃料电池的输出电压不够,影响电动汽车系统的运行.当电动汽车制动时,双向DC-DC变换器工作在BUCK模式下,制动过程所产生的能量通过双向DC-DC变换器流向蓄电池,为蓄电池充电[4].
全文HTML
-
根据对开关电路的理想化方法和抽象程度,可以建立3个不同层次的开关电源模型,包括开关模型、状态空间平均模型和小信号模型[5-7].其中,开关模型所建立的系统是非线性时变系统,需要通过将方程简化为线性定常的方程来确定解析解.通过对理想开关模型在开关处于开通或者关断时的方程进行加权平均处理,得到近似的平均状态方程.开关电源的控制是通过改变PWM波占空比来实现的,PWM波的占空比为开关电源的一个随着时间变化而变化的输入量.这种情况下,状态变量和控制变量之间有乘积项,也就是存在耦合[8],此时,状态空间平均模型不是线性的,所以通常需要对系统进行局部线性化,即得到小信号模型.
-
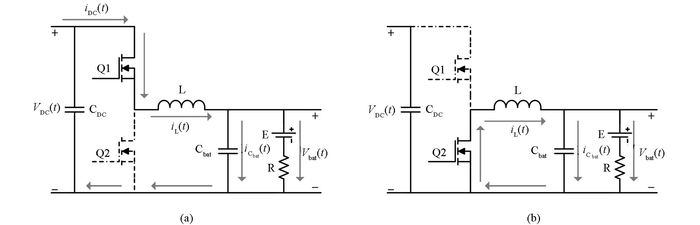
本设计充电模式选择恒流充电.当双向DC-DC电源在恒流充电模式下工作时,双向DC-DC的工作模式为BUCK降压模式,作为电池的负载可以使用电池的简化模型进行模型的建立.在BUCK降压模式下,电源工作在电感电流连续(CCM)模式,每一个周期电源都会有两个不同的状态[9],如图 2所示,设图中元件均是理想器件,忽略寄生参数影响,开关周期为T,占空比为d,建立直流输入电压VDC(t)作为输入变量,输入电流iDC(t)和电池两端电压Vbat(t)作为输出变量,输出电容电压VCbat(t)和电感电流iL(t)作为状态变量的小信号模型[10].
如图 1(a)所示,当Q1导通、Q2关断时将导通和关断得到方程进行加权平均处理并引入小信号得到输出方程:
电池端电压
$V_{\rm{bat}}^{\hat{\ }}\left( s \right)$ 对占空比$d\hat{(}s)$ 的传递函数${{G}_{{{V}_{\rm{bat}}}}}_{d}^{\hat{\ }}\left( s \right)$ 为电感电流
${{i}_{\rm{L}}}\hat{(}s)$ 对PWM占空比$d\hat{(}s)$ 的传递函数${{G}_{{{i}_{\rm{L}}}}}_{d}^{\hat{\ }}\left( s \right)$ 为 -
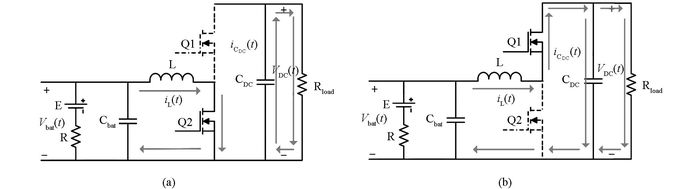
当双向DC-DC电源在BOOST模式下时,电源工作在电感电流连续(CCM)模式[9].每一个周期电源都会有两个不同的状态,如图 3所示,设图 2中所有电子元件均是理想器件,开关周期为T,占空比为d,建立小信号模型.
同上,将导通和关断得到方程进行加权平均并引入小信号处理并得到输出方程:
电感电流
${{i}_{\rm{L}}}\hat{(}s)$ 对PWM占空比$d\hat{(}s)$ 的传递函数${{G}_{{{i}_{\rm{L}}}}}_{d}^{\hat{\ }}\left( s \right)$ 为
1.1. 双向DC-DC电源恒流充电数学模型
1.2. 双向DC-DC电源恒压放电数学模型
-
经过前面的小信号模型分析,输出电压对占空比的传递函数为
充电电流为
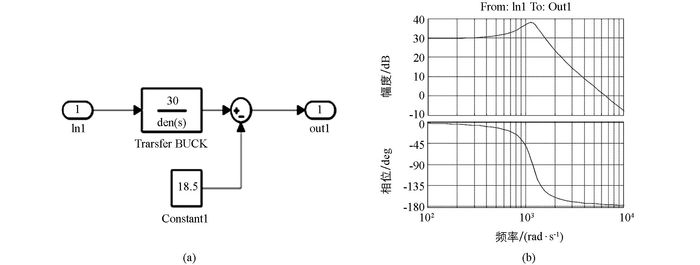
本文设计所采用直流侧电压为30 V,电感参数为330 uH,电容参数为2 200 uF.建立Simulink数学模型如图 4(a)所示[11],BUCK模式下的开环伯德图如图 4(b)所示.
当双向DC-DC变换器工作在BUCK模式下,系统的传递函数是一个二阶的振荡环节,为了更好补偿共轭极点造成的相位滞后,控制器的一个零点z1应在谐振频率
$1/\sqrt {LC} $ 处[12],控制器的第二个零点z2应选择在距离共轭极点很远的位置处,提供更多的超前相位,一般选取在1/10的共轭极点频率处.选择系统的控制器为PID控制器,其传递函数为
式中:τ1、τ2是PID控制器的零点:
开关电源传递函数的谐振频率
$1/\sqrt{\rm{LC}}=1/\sqrt{330*{{10}^{-6}}*2200*{{10}^{-6}}}=1173.6\ \rm{rad}/\rm{s}$ ,取PID控制器的第一个零点在开关电源传递函数的谐振频率处,第二个零点在开关电源传递函数的谐振频率的1/10处,即取z1=1 173.6 rad/s,z2=117.36 rad/s,
则:
得到传递函数:
对应的
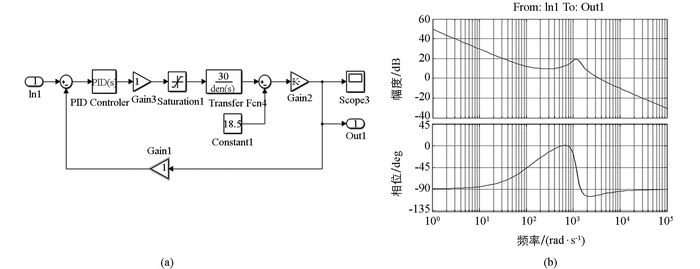
${{G}_{\rm{PID}}}\left( s \right)={{K}_{P}}+\frac{{{K}_{I}}}{s}+{{K}_{{{D}^{S}}}}$ ,其中KP=0.000 083 24、KI=0.008 881、KD=0.000 000 064 5.加入PID控制器,闭环负反馈系统的数学模型如图 5(a),开环伯德图如图 5(b)所示.从图 5(b)中可以看出,系统穿越频率[13]在3 500 rad/s附近,穿越斜率为-20 db/dec,相位裕度>450,满足稳定条件,可以分析得出系统稳定.
-
经过前面的小信号模型分析,输出电压对PWM占空比的传递函数为
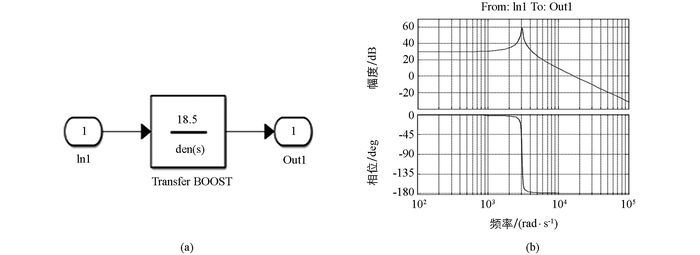
本文设计所采用电感参数为330 uH,电容参数为330 uF,电池两端电压18.5 V左右.电感初始电流IL=0,初始占空比D=0.则传递函数为
用Matlab中的Simulink建立其数学模型如图 6(a)所示,BOOST模式下的开环伯德图如图 6(b)所示.
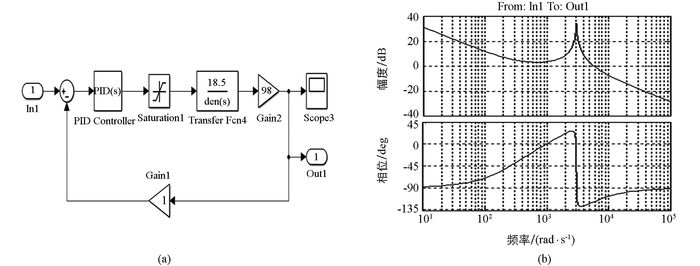
此模型与BUCK电路的模型类别一致,传递函数均为二阶振荡环节,按照上一节给出的计算PID参数方法,得到参数:KP=0.000 740 8、KI=0.204 1、KD=0.000 000 222,加入PID控制器,闭环负反馈系统的数学模型如图 7(a),开环伯德图如图 7(b)所示.从图 7(b)可以分析得出,系统穿越频率在5 000 rad/s附近,穿越斜率为-20 db/dec,相位裕度>45,满足稳定条件系统稳定.
2.1. 双向DC-DC电源恒流充电控制器的设计与仿真
2.2. 双向DC-DC电源恒压放电控制器的设计与仿真
-
双向DC-DC电源广泛应用于电动汽车、UPS(不间断电源)、光伏并网系统、和分布式电站、轨道交通等众多领域中.在本文设计选用双向半桥型开关电源拓扑作为系统的主电路设计方案,同时使用同步整流技术进一步提高了双向DC-DC电源的效率.运用开关电源相关知识对双向DC-DC电源进行了数学模型建立及仿真,分析并验证了PID控制器在开关电源控制中的正确性.同时利用Matlab编程计算设计参数、simulink仿真验证参数设计的合理性,完成了对开关电源理论的基本分析和验证.



 下载:
下载: