-
对城市演化的模拟研究从上世纪60年代以来一直是地理科学研究的重要问题,其中一个主要方法是元胞自动机(cellular automata,CA).在20世纪70年代,Tobler就将CA应用到美国五大湖地区底特律的城市扩展模拟中[1].随后CA被广泛应用于城市模拟研究中[2-4],并将CA策略与地理信息系统(geographic information system,GIS)技术结合起来,用于模拟空间复杂的起源与演化.近年来,越来越多的人将GIS技术和人工智能算法相结合来解决复杂地理问题,如将粒子群优化算法与多智能体方法相结合,用遗传算法来获取CA模型的最佳参数,利用蚁群智能算法挖掘CA的转换规则等[5-10].可见将人工智能算法与CA相结合,是目前也将是未来地理领域解决复杂问题的主要策略.
在以往,用地转换规则提取与城市演化模拟中存在着一些不足,比如:在粒子群优化模型中,粒子不断地优化其所在空间时,计算量就会随着图斑数表现出几何级增长[5];使用逻辑回归模型时,要求解释变量之间线性无关,但实际模拟中,很多解释变量有很大的线性相关性,这直接影响了模拟精度[6];在决策树模型中,以熵作为局部启发度量,很容易受到各属性之间的影响,特别是数据属性的相关性比较大的时候,就可能出现局部最优解[7].
近年来,国内外学者致力于特征提取方法的研究,取得了较好的效果[11-16].用地分类的多样性会影响分类的均衡性,关于用地分类的均衡性目前少有提及.针对传统模型对用地转换规则提取的准确性,以及分类均衡性问题,本文拟将DBN与地理元胞自动机(geographical cellular automata,GeoCA)相结合,构建整合模型实现用地转换规则的提取以及城市演化模拟,同时采用多方案对比法检测网络层深度以及用地分类的均衡性对模拟精度的影响.
全文HTML
-
深度信念网络由多层无监督的受限玻尔兹曼机(restricted Boltzmann machine,RBM)和一层有监督的反向传播(back-propagation,BP)网络组成.
-
RBM是在玻尔兹曼机(Boltzmann machine,BM)的基础上发展来的,BM是由随机神经元(Sigmoid函数)组成的具有随机性的机器.在网络训练阶段,可见层神经元的状态由训练条件所决定,而隐含层神经元可以根据自身的条件完成学习过程.学习过程采用最小能量函数求解,观测数据通常会被用来对模型进行最佳拟合计算和最小似然函数计算,其似然函数也是通过能量函数来提供的.在RBM中,输入层向量v和隐含层向量h之间的能量函数为:
其中:v表示可见层状态,h表示隐含层状态,vi表示第i个可视节点状态,hj表示第j个隐含节点状态.每个节点都有指定的状态,RBM则有对应的能量,所有节点对应某一状态即是一个整体状态,穷举所有配置对应的能量之和为归一化常量Z.得到RBM的取样概率为:
式(2)中,
-
训练BP网络可以分为前向传播和后向传播2个过程.前向传播时,输入特征向量会被逐层传播到输出层,得到预测的分类结果,将期望分类结果与实际得到的分类结果进行比较,得到训练误差,再将误差逐层向后回传,以微调DBN的训练参数.后向传播时,需计算每层网络的灵敏度数值,灵敏度被自顶向下传递,用来校正网络的权值参数.在输出层,如果第i个节点的实际输出为oi,期望输出为di,那么灵敏度δ的计算公式表示为:
对于第l个隐含层,δ的计算公式为:
得到各网络层的灵敏度δ之后,DBN的网络权值即可更新,以此来完成网络的训练[16].
-
CA是离散的动态模型,其数学定义包含{L,S,N,Fn}4个要素,L是在空间中的网格;S={S0,S1,…,Sn},是有限的状态集;N={N0,N1,…,Nk},是一组有限的邻域集;Fn:Sn→S是一个过渡函数.用CA做离散计算时,预定义的元胞集通过一组规则来实现自身的演化和相互之间的作用[20-21].其自下而上的计算演化策略、宏观和微观元胞之间的相互联系,使得CA适用于各种领域,包括数值分析、流体动力学、模拟生物和生态系统等领域[22].
1.1. 受限玻尔兹曼机
1.2. BP网络
1.3. 元胞自动机
-
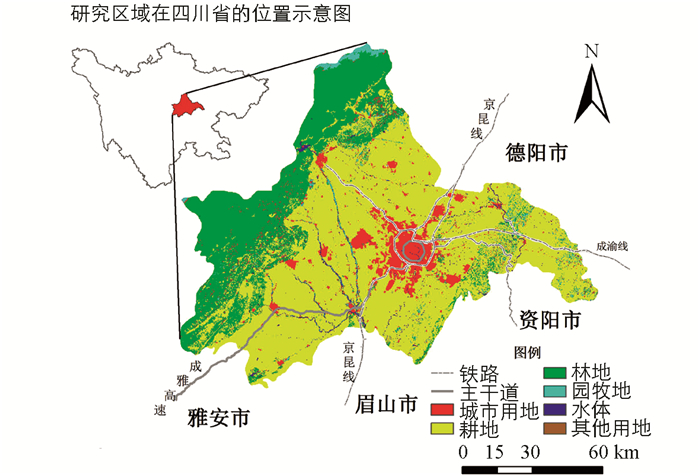
本文所选研究区域为四川省成都市,是西南地区的科技、商贸、金融中心和交通、通讯枢纽,是一个典型的平原城市,总面积达12 390 km2,位于四川省的中部地区.成都市作为我国西部大开发的战略高地,在过去15年中实现了经济的跨越式发展,在未来发展中,成都市将会增强其集聚辐射能力,以应对当今全球化的经济发展趋势.成都市的区位及空间格局如图 1所示.
-
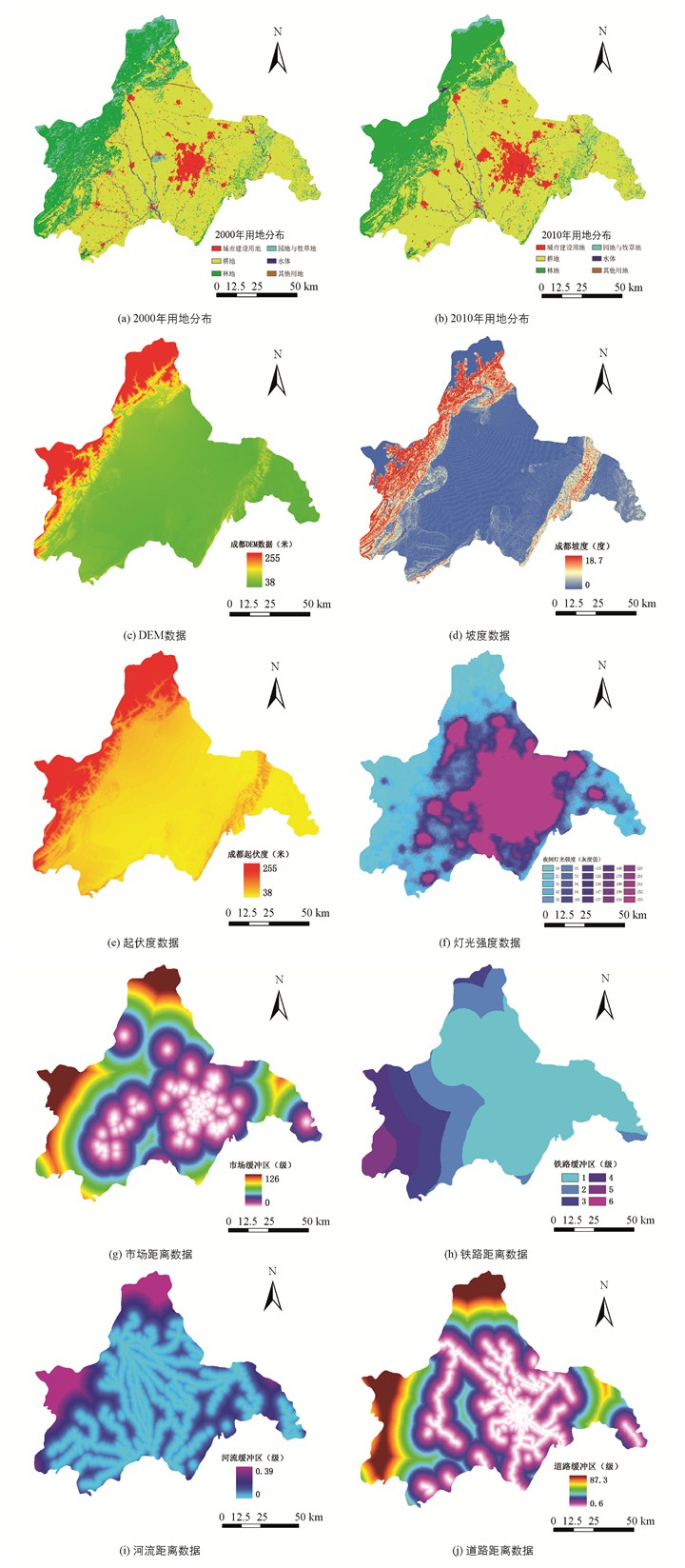
本文所用的2000年用地类型数据由TM遥感数据在ENVI上分类得到,2010年的用地类型数据是通过向全球地表覆盖数据产品申请而免费获得(网址http://www.globallandcover.com/GLC30Download/index.aspx),使用这两期数据得到研究区域10年间的用地变化情况.数据分辨率为200 m,成都市包含304 801个栅格.将现有的用地类型分别分类为6种用地类型(表 1),4种用地类型(将表 1中的园地与牧草地、水体和其他用地合并为一种用地类型)和2种用地类型(城市建设用地和非城市用地). 2000年至2010年成都市用地变化检测结果如表 1所示.从表 1中可以看出2000年至2010年建设用地增加4 271个栅格;耕地减少2 223个栅格;林地增加9 269个栅格;园地与牧草地减少10 833个栅格;水体增加282个栅格;其他用地减少766个栅格.
构建城市模拟模型时,驱动因子的准确性与显著性会影响模拟精度.驱动因子包括地面坡度、河流、地貌环境以及在这些因素的作用下形成的交通布局等[23-24].根据成都市的特点,本文选择了DEM高程数据、坡度、起伏度、夜间灯光强度以及与河流、铁路、道路、市场之间的距离等8个驱动因子.
驱动因子数据中,高程数据(DEM)来自美国马里兰大学地球科学数据集(ftp://ftp.glcf.umd.edu/glcf/GLSDEM/),由DEM数据可以计算得到起伏度和坡度数据.考虑到夜间灯光强度与人口密度具有高度的相关性,因此用夜间灯光强度代表人口密度,其数据由NASA在2000年拍摄的全球夜间灯光数据用成都市的矢量裁剪而得.成都市行政界线矢量数据和交通数据来自开放街景地图(http://www.vdstech.com/osm-data.aspx),其中距河流和道路的距离缓冲区通过加权计算得到.计算河流缓冲区时一级河流权重70%,二级河流权重30%;道路缓冲区计算中主干道路权重40%,一级道路权重25%,二级道路权重20%,三级道路权重15%.将各驱动因子数据与两期用地分布数据统一地理坐标、地图投影、研究范围和分辨率,形成统一的空间数据库,这些处理过程均在ArcGIS平台完成.两期用地空间分布如图 2(a)-(b)所示,驱动因子空间分布如图 2(c)-(j)所示.
-
本文对用地转换规则的提取是通过对DBN的训练来完成的.数据处理、网络训练和结果表达用地理信息系统软件与MATLAB软件相结合来实现.首先在ArcGIS上将已经处理完成的驱动因子数据、两期用地分布数据和用地变化数据转为点数据,一个点代表一个元胞.之后在SPSS软件中将驱动因子和前期用地分布点数据组合成一个矩阵,作为网络训练的输入数据.将矩阵数据导入到MATLAB中,通过编程在MATLAB上完成DBN的学习与模拟过程,学习得到的每个驱动因子引起用地类型发生变化的作用规则被以数学的方式记录在神经元中,将训练完成的网络保存下来进行预测模拟.最后将模拟结果用SPSS转化为ArcGIS可识别的点数据格式,导入到ArcGIS中将模拟结果进行可视化地图表达.
本文采用多方案对比法检测网络层深度以及用地分类均衡性对模拟精度的影响,设计了两种实验方案:首先,将成都市分别分为2类用地(城市和非城市用地)、4类用地(城市用地、耕地、林地、其他用地)和6类用地(城市用地、耕地、林地、园地与牧草地、水体、其他用地)的情况依次模拟,对比结果,检验用地类型数量变化时模拟结果总体精度的变化;其次,每一种实验方案中,均设定了隐层网络分别为2层、3层、4层、5层、6层的情形,根据其模拟结果的总体精度变化,探索网络层深度对模型模拟精度的影响.根据White研究所得的隐层神经元数目计算公式:
其中:S表示隐层神经元数目,k为输入层神经元数目,n为输出层神经元数目[25].
根据反复试验,本文所有方案中,网络训练采用的迭代次数为6 000次,输入层为所有驱动因子和2000年的用地类型数据,共含9个神经元.用地变化检测数据作为输出层,含1个神经元.根据White研究所得公式计算,隐含层设置6个神经元.
2.1. 研究区域概况
2.2. 数据采集与处理
2.3. 实验方案设置与用地转换规则提取
-
Cohen在1960年提出了Kappa系数这一概念,通过对地面调查的地物类别数据和遥感影像分类结果数据建立混淆矩阵,用来评价遥感影像的分类结果与实际用地类型的一致性程度[26]. Kappa系数的计算公式为:
其中P0和Pe的计算公式分别表示为:
式(6)中:P0表示遥感数据分类的总体精度,即对于每一个栅格的分类结果与实际用地类型相一致的概率值,Pe表示分类用地类型结果与地面调查用地类型相一致的概率值.式(7)是P0的计算公式,式(8)是Pe的计算公式,n为用地分类的类型种数,N为检测数据的总数量,Pii表示第i类用地被正确分类的数目,Pir表示第i类用地所在列的栅格数目之和,Pic表示第i类用地所在行的栅格数目之和.利用Cohen提出的Kappa系数分类评价标准对模拟结果进行一致性评价[27-28],其标准如表 2所示:
同时可以对每种用地类型计算Kappa系数,计算公式为:
式(9)中:Pii表示该用地类型的模拟结果与实际用地相一致的栅格数与该区域总栅格数的比值,Pir表示该用地类型实际用地栅格数与该区域总栅格数的比值,Pic表示模拟的该用地类型栅格数与该区域总栅格数的比值.
-
在相同硬件环境下完成实验,根据实验结果数据,得到一致性评价结果如表 3所示.
根据表 3模拟结果可以得出以下结论:
1) 网络深度对网络性能有影响.从总体模拟结果看,驱动因子相同时网络深度对网络性能有较大影响,总体上层数较高模拟效果越好,但也不是越深越好.如表 3所示,在3种不同用地分类实验中,隐含层含有5层网络时总体Kappa值最高,因此在模拟时有必要进行多层网络试验.隐层网络数目与模拟结果Kappa值的关系如图 3所示.
2) 用地分类种数对模拟精度有影响.将研究区域分为2种用地、4种用地和6种用地分别实验,检测模拟精度可知,在网络隐含层数目相同时,分为4种用地时总体Kappa值最高,分为6种用地时次之,分为2种用地时最低.
3) 网络隐层数目与模拟时长之间的关系.实验表明,随着网络隐层数增加,迭代相同的次数所需的时间也随之增加.以6种用地分类为例,在相同的运行环境下,隐层数是2时,模拟时间是4.82 h;隐层数是3时,模拟时间达8.12 h;隐层数是5时,模拟时间达14.07 h.可见学习过程会随着网络层数的增加而更加复杂,所需计算时间也会越长.
-
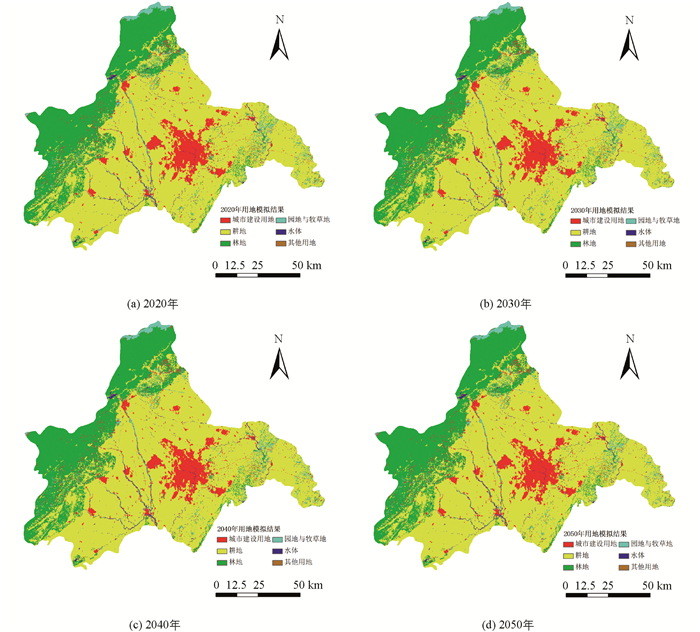
综合考虑,将用地分为6种类型的时候,对用地发展的研究具有较高的实用性.用地类型分为6种且隐含层含有5层网络时网络具有最好的综合性能,因此使用该网络模拟出了成都市在现有发展条件下后期40年的用地空间分布,模拟得2020年至2050年成都市各类用地的栅格数目如表 4所示,用地空间分布如图 4(a)-(d)所示.
3.1. 精度评价方法
3.2. 实验结果分析
3.3. 城市扩展模拟
-
本文完成了两方面的工作,一是以成都市为例,使用DBN与GeoCA相结合构建的模型,较好地提取了用地转换规则,模拟用地总体Kappa值达到了80.82%;二是用多方案对比法检测网络层深度以及用地分类均衡性对模拟精度的影响.当网络隐含层数目相同,划分为4类用地时总体Kappa值最高,划分为6类、2类用地时总体Kappa值依次递减.出现这种结果的主要原因在于各种用地类型在成都市所占的面积比例不同,如果某类用地的元胞数量多,其转换规则就能够更完全地被提取,4类用地时各类用地比较均衡,所以会有最高的总体Kappa值.
与此同时,本文以经济持续增长为发展情景,模拟了成都市未来40年的用地空间分布,结果表明在现有驱动城市演进因子的作用下,即使成都市保持现在的经济发展速度,成都市未来40年之内的城市用地也不会以现有的增长率增长,而是会低于其2000年至2010年的增长速度,逐渐放缓增长.
本文方法在用地转换规则的提取方面取得了较好的效果,但用地分类的均衡性对模拟结果的影响也不容忽视.成都市是典型的平原城市,考虑到的驱动因子也存在着区域性,对成都市未来的用地模拟中,也未考虑驱动因子的变化.该模型能很好地模拟旧城市的扩张,但对新城市的诞生没有很好的模拟机制.后续工作中,将围绕以下3个方面进一步研究:①改进现有的模型,使其能够更彻底地消除用地分类的不均衡对模拟结果的影响,并挖掘出研究区域新城市的发展潜能,构建新城市的诞生机制;②更多地考虑城市地理因素,从单一的城市类型过渡到更多类型的城市,比如山地城市等;③深化驱动因子的选取,特别是在研究区域后期模拟中,需要考虑随时间推移而发生变化的驱动因子对城市演化的影响.



 下载:
下载: