-
颚式破碎机自1858年由E.W.Blake发明以来,已有150多年历史,按动颚运动特点,颚式破碎机分成简摆式与复摆式两种基本类型,复摆式颚式破碎机由于其结构简单、经济性、操作性好等诸多优点,是目前国内生产最多、使用最广的破碎设备[1].
衬板磨损是颚式破碎机的主要问题,通常可采用降低动颚运动特性值来解决其磨损问题[2-3].母福生等人利用离散元法获得齿板齿形参数对破碎力的影响规律[4].黄大明等人以惯性力引起的附加动载荷为出发点,分析运动副之间约束力及平衡力矩,利用MATLAB程序求解各构件在机构运动中的受力大小及变动规律[5].姜丹丹等人利用ABAQUS软件对动颚齿板进行有限元分析,计算出了动颚齿板在工作过程中所受的最大破碎力值,得到动颚的应力分布情况[6].李刚等人利用ADAMS软件对复摆颚式破碎机进行了动力学仿真分析,从工作平稳性以及可靠性两方面对破碎机进化优化[7].王晓敏等人对PE400×600复摆式颚式破碎机进行仿真优化,通过改变参数点的位置来改变机架的位置进行优化设计[8].张德浩等人研究了锤式破碎机的主轴辊模态特性,并通过模态测试分析主轴辊模态参数,对主轴辊有限元分析模型进行了验证[9].
动颚的垂直行程使得动颚与定颚间产生垂直方向的相对运动,这种相对磨搓运动加剧动颚与定颚衬板的磨损,降低了衬板的使用寿命.本文以降低动颚下部运动特性值为目标,在分析破碎机运动特点的基础上,提出基于遗传算法的复摆颚式破碎机尺寸优化方法.
全文HTML
-
复摆式破碎机机构类型是曲柄摇杆机构,动颚上的点一般作复合平面运动,轨迹近似为封闭椭圆曲线,进料口处轨迹为椭圆形,越靠近排料口其椭圆轨迹形状越趋于扁直,排料口处的沿水平方向位移与垂直方向位移分别称作动颚水平行程Sx与动颚垂直行程Sy,二者比值Sy/Sx即为动颚运动特性值.
动颚水平行程可以产生破碎物料所必须的压缩量,降低动颚运动特性值必须要充分考虑满足破碎矿石压缩量,在此基础上最大限度降低动颚垂直行程[10].为建立以动颚运动特性值为目标函数的优化模型,利用解析法对颚式破碎机进行运动学分析,可精确求解动颚水平行程与垂直行程.
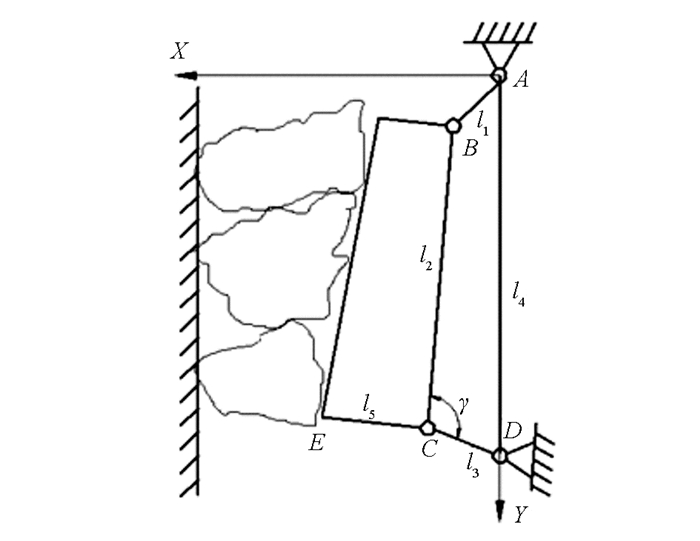
复摆式颚式破碎机的机构简图如图 1所示.曲柄AB、连杆BC、肘板CD和机架AD长度分别是l1,l2,l3,l4,动颚下端宽度为l5.其中θ1,θ2及θ3分别是构件1,2和3相对于X轴的角位移.
以曲柄转动中心为坐标原点,建立直角坐标系,通过杆矢量建立机构封闭矢量位置方程:
将封闭矢量以复数矢量法表示,则(1)式和(2)式可表示为
利用方程3与方程4求得动颚齿板E点运动轨迹坐标为
计算出E点两极限位置横坐标之差,即得到动颚下部水平行程Sx:
计算出E点两极限位置纵坐标之差,即得到动颚下部垂直行程SY:
-
利用动颚运动轨迹分析结果,计算得到动颚运动特性值f(x):
优化模型以动颚运动特性值最小为最优,目标函数Q表示为
-
影响颚式破碎机结构尺寸的主要独立参数有:曲柄l1、连杆l2、肘板长度l3、两固定铰链距离l4和下部动颚宽度l5.则设计变量X表示为:
-
破碎机整体机构尺寸在满足动颚运动特性值最小的前提下,必须考虑到生产能力、机构力学性能等因素,为此建立包含构件尺寸、工作参数匹配、腔形参数合理等3类约束条件:
第Ⅰ类约束:构件尺寸约束
各构件参数取值范围直接影响优化结果,采用经验类比方法,确定各构件尺寸取值区间.设计变量的取值范围如表 1所示:
对于复摆式破碎机,曲柄与肘板较连杆和机架长度小得多,四杆机构存在曲柄的约束条件可简化为两个:
第Ⅱ类约束:工作参数匹配
生产率作为颚式破碎机重要性能指标,直接决定破碎机生产能力.基于动颚运动特性值的优化必须充分考虑到破碎机生产能力,才能使破碎机性能达到整体最优.增大主轴转速可提高生产能力,但与其匹配的动颚下部水平行程必然会减小,从而又降低生产能力.为提高破碎机生产能力,使转速n、啮角α以及动颚下部水平行程Sx这3个参数相互匹配,建立以下约束:
第Ⅲ类约束:腔形参数合理
为满足四杆机构力学性能,机构在运动过程中其最小传动角应大于40°或50°,当曲柄与机架两次共线时,机构可能会出现最小传动角,其值分别等于γ1和γ2,以两值之中的最小值作为最小传动角γmin.
确定最小传动角约束条件:
动颚衬板挤压物料过程中,要求衬板与物料间产生的摩擦力足够大,以防止矿石被向上挤出.因此确定啮角约束条件为
-
通过目标函数及约束条件,建立变量为5维,具有17个不等式约束及1个等式约束的颚式破碎机非线性优化设计模型如下:
2.1. 目标函数
2.2. 设计变量X
2.3. 约束条件
2.4. 优化模型
-
利用Matlab软件对机构进行运动学分析,得到在一个工作循环内动颚下端E点运动轨迹坐标,在此基础上采用遗传算法工具对模型进行优化,优化模型以获得最小目标函数值为最优.而遗传算法的适应度函数以最大值为最优,需将解空间中的目标函数转换为遗传算法中的适应度函数,适应度函数Fit(f(t))如下[11]:
其中c>0,c+f(x)>0,c为目标函数f(x)的保守估计值.
设置遗传算法参数如下:代沟为0.9,群体规模为100,交叉概率为0.9,变异概率为0.2,终止进化代数为100.优化前后机构尺寸参数对比如表 2所示,优化前后破碎机产品性能对比如表 3所示.
由表 3可知,优化后排料口水平行程比优化前增大7.66%,排料口垂直行程减小7.03%,运动特性值降低幅度为13.84%,达到优化设计目的.优化后机构最小传动角比优化前略有降低,降低5%.增大传动角固然对力学性能更加有利,但是增大传动角必然会增大垂直行程,而且会使水平行程降低,优化后最小传动角为50.05°,满足其自身约束条件.
优化模型中的第Ⅱ类约束条件,即工作参数匹配的要求,使啮角与动颚下部水平行程及主轴转速3种参数间匹配更加合理,优化后平均啮角比优化前减小近20%,在此基础上确定出匹配的主轴转速为285 r/min,由表 3中优化前后对比可知,优化后破碎机生产能力比优化前提高近12.37%.
-
本文在利用解析法对破碎机进行运动学分析基础上,构建基于遗传算法的破碎机优化数学模型,对PE250×400型复摆式破碎机尺寸进行优化,优化后动颚水平行程增大,垂直行程减小,使动颚运动特性值随之减小,改善了动颚衬板的磨损,优化后机构的动颚水平行程,啮角与转速这3个参数满足相互匹配要求,提高了破碎机生产率.本文提出的基于遗传算法的破碎机优化设计方法在减小运动特性值同时又提高了生产率这一关键指标,满足破碎机优化设计要求.



 下载:
下载: