设X₁，X₂，…，X_n是随机变量序列，若满足

(1) E({X_n})=u；

(2) cov(X_n，X_n-l)=σ₁；

则称序列{X_n}是协方差平稳的(弱平稳).本文主要考虑弱平稳序列且M_n=max(X₁，X₂，…，X_n).

文献[6]弱化了Rosenblatt(1956)提出的强混合条件，引入D(u_n)和D'(u_n)条件讨论平稳序列的极值理论. D(u_n)条件表示平稳随机变量序列的渐近独立性，D'(u_n)条件则表示平稳随机变量序列中极端观测值接近的概率可渐近忽略.

满足D(u_n)和D'(u_n)条件的平稳随机变量序列极值的渐近分布服从广义极值分布(GEV)：

其中：μ为位置参数，σ为尺度参数，γ为形状参数.

D(u_n)条件实质很弱，容易满足，但是D'(u_n)条件对多数序列并不合理，常常出现成串的极大值.极值指标θ能反映序列数据的相依结构和极端情况之间的关系，下面给出极值指标的定义.

定义1  设X₁，X₂，…，X_n为平稳随机序列，其分布函数为F(x)，θ为非负数，若对任意τ＞0存在序列{u_n}满足

(1) $ \mathop {\lim }\limits_{n \to + \infty } nF\left( {{u_n}} \right) = \tau $，

(2) $ \mathop {\lim }\limits_{n \to + \infty } P\left( {{M_n} \le {u_n}} \right) = {{\rm{e}}^{ - \theta \tau }} $，

则称θ为平稳随机序列{X_n}的极值指标，且θ∈[0, 1].

设$ \widetilde {{X_1}}, \widetilde {{X_2}}, \cdots , \widetilde {{X_n}} $是独立的随机变量序列，若序列$ \left\{ {\widetilde {{X_n}}} \right\} $中每一个随机变量$ {\widetilde {{X_i}}} $都与平稳随机序列$ \left\{ {\widetilde {{X_n}}} \right\} $中随机变量X_i相互对应且具有相同的分布，则称序列$ \left\{ {\widetilde {{X_n}}} \right\} $为平稳随机序列{X_n}的伴随独立同分布序列.

文献[7]得到了基于极值指标下平稳随机变量序列极值的渐近分布和与其相伴的独立同分布序列极值的渐近分布之间关系的结论.

定理1^[7]  存在常数列{a_n＞0}和{b_n}，以及非退化分布函数$ \widetilde {{F_ * }}\left( x \right) $使得P{a_n(M_n-b_n)≤x}→$ \widetilde {{F_ * }}\left( x \right) $，n→∞.若对于每个x有D(u_n)条件成立，其中u_n=a_nx+b_n，使得$ \widetilde {{F_ * }}\left( x \right) $＞0，且对某个x，P{a_n(M_n-b_n)≤x}收敛，则对于某个常数θ∈[0, 1]，有P{a_n(M_n-b_n)≤x}→F_*(x)=$ {\widetilde {{F_ * }}^\theta }\left( x \right) $，n→∞.

定理1说明通过极值指标θ，可以将平稳随机变量序列极值的渐近分布拟合问题转化为与其相伴的独立同分布序列极值的渐近分布拟合问题.设独立同分布序列$ \left\{ {\widetilde {{X_i}}} \right\} $，$ {\widetilde {{X_n}}} $服从位置参数为b，尺度参数为a，形状参数为γ的GEV分布.根据定理1可得

其中

对极值指标为θ且满足D(u_n)条件的平稳随机序列{X_n}，其样本最大值的渐近分布是形状参数为γ的广义极值分布，与独立同分布的随机序列相同，而位置参数a_*和尺度参数b_*均受序列数据自身相依性的影响，与极值指标有关.

平稳时间序列极值指标θ的估计有区组法、平均法.区组法根据极值指标定义变形得到

利用样本信息划分为每组样本量为k的$ \frac{n}{k} $组，且$ g = \left[ {\frac{n}{k}} \right] $.有估计量

其中：N(u_n)为样本中大于门限u_n的样本点个数，G(u_n)为各组最大值大于门限u_n的组个数.平均法即是在区组法估计量之上对分子分母分别作一阶Taylor展开得到估计量

为给出极值指标下平稳随机序列的风险测度，先给出VaR的定义. VaR表示在给定置信水平下，某一资产组合的最大损失值.金融市场中VaR能兼顾风险发生的概率水平和损失程度，被视为风险管理主要指标，用于度量金融机构所面临的信用风险、市场风险和操作风险这3类主要风险.

定义2  对给定p∈(0，1)，VaR定义为：P(ΔX≥VaR)=1-P(ΔX＜VaR)=p，ΔX表示资产的改变量(损失量).

利用BMM方法，假设每个子样本(长度为n)极值服从GEV分布，可以得到形状、位置、尺度3个参数估计值：$ \hat \gamma , \hat a $和$ \hat b $.对独立同分布收益率序列$ \left\{ {\widetilde {{X_n}}} \right\} $，令概率p^*表示一个多头头寸潜在损失超过一定限度的可能性，且x_n^*是在子样本最小值渐近分布为GEV分布条件下的(1-p^*)分位数，即有

取对数，反解x_n^*得到

在收益率序列样本X_t独立同分布假设下，样本X_t和其子样本{x_n，n}之间关系为：

则对给定概率p，持有对数收益率X_t资产的VaR为：

在收益率序列样本X_t满足D(u_n)条件且平稳的假设下，令极值指标为θ(θ∈[0, 1])，样本X_t和其子样本{x_n，n}之间关系为：

则对给定概率p，持有对数收益率X_t资产的VaR为：

由极值指标取值范围知，如果忽略序列数据相依性，平稳随机变量序列的风险值存在低估的风险.

下面给出极值指标下平稳随机序列风险测度的应用.

选取我国股票市场具有代表性的上证综指作为实证对象，考虑到风险测度方法主要用途是预测和量化下一期风险程度，将样本划分为2个部分，其中2010年1月4日至2015年12月31日的上证综指收盘价格作为研究样本用于模型拟合和VaR估计，样本容量1455；2016年1月4日至2016年12月1日的上证综指收盘价格作为检验样本用于VaR预测效果评价，样本容量222.样本来源于上海证券交易所公开数据，采用R软件进行数据处理和统计分析.

定义收益率：

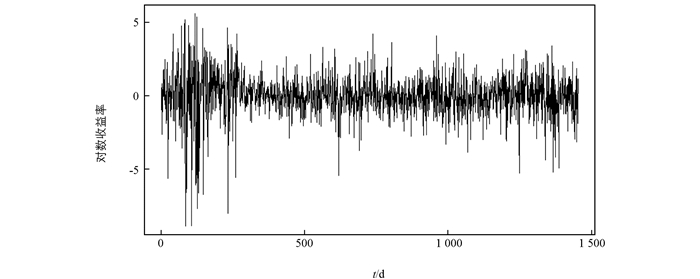
其中P_t表示上证综指第t日收盘价格，其基本统计特征见表 1，时序图见图 1.

由表 1可知上证综指收益序列{X_t}的峰度值和偏度值.与正态分布比较，上证综指收益序列呈现尖峰厚尾、左偏的分布形态.由图 1可知序列还存在波动率聚集效应.采用ADF检验和BDS统计量分别考察序列的平稳性(表 2)以及序列自身数据的独立性问题(表 3). ADF检验统计量为-10.876，在5%显著性水平下拒绝“序列存在单位根”的原假设，即{X_t}是平稳的.二维、三维BDS统计量分别为2.390 8和3.299 5，在5%显著性水平下拒绝“序列数据独立”的原假设，说明序列数据自身存在相依性，在平稳序列的极值建模和VaR估计过程中不能忽略这一问题.

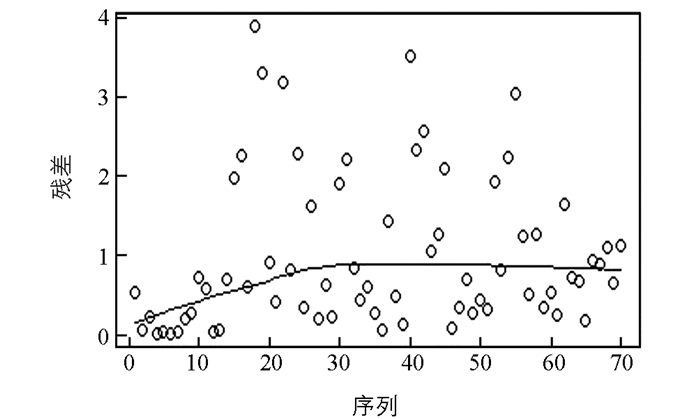
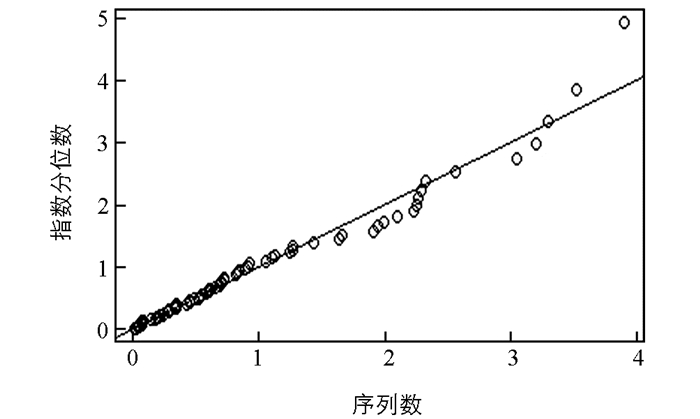
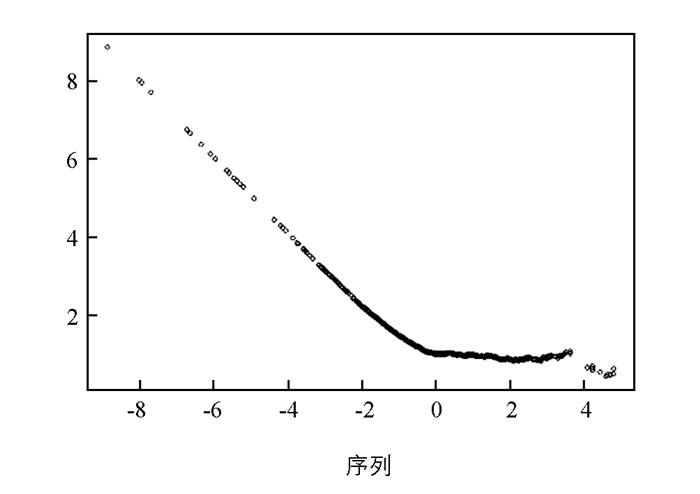
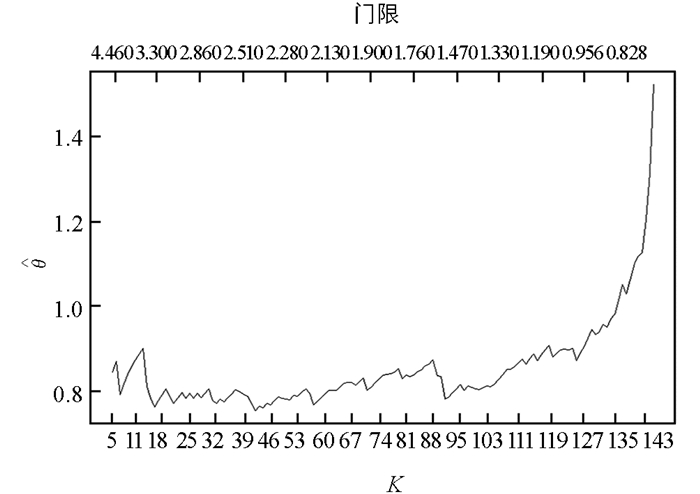
选用BMM对上证综指收益序列{X_t}的极值分布进行GEV拟合，根据股票平均月度交易天数约为21天划分子样本，取n=21. GEV拟合的最大似然估计具有无偏、渐近正态这样的优良性质，得到估计值$ {\hat \varepsilon } $=0.059 567 76，$ {\hat a} $=0.785 868 15和$ {\hat b} $=1.984 635 97. GEV拟合的残差图(图 2)和对指数分布QQ图(图 3)表明模型拟合合理，子样本容量取值合理.

根据序列相依性取k=10，利用组方法估计极值指标.分别考察基于样本数据的平均超越函数图(图 4)和极值指标估计图(图 5)以确定门限和极值指标的估计值.可知门限2.5附近样本平均超越量函数斜率为正且线性变化，而对应的极值指标估计值$ {\hat \theta } $=0.8.

为对不同风险测度的准确性进行检验，计算在未引入极值指标和引入极值指标两种情况下上证综指收益序列{X_t}的VaR₁和VaR₂.由公式(1)得到未引入极值指标下5% VaR₁值为1.926 4，表示假设上证综指资产组合的多头头寸为100万人民币，其相应的多头头寸在1天持有期内的5% VaR为19 264元.同样，由公式(2)得到引入极值指标($ {\hat \theta } $=0.8)下，5% VaR₂为2.102 1，表示假设上证综指资产组合的多头头寸为100万人民币，其相应的多头头寸在1天持有期内的5% VaR为21 021元.

采用Kupiec失败频率检验法对检验样本进行测试.记损失量超过VaR估计量为失败，记损失量低于VaR估计量为成功，设考察总天数为T，失败天数为N，失败概率为$ p = \frac{N}{T} $，而在置信水平q下失败的期望概率为$ \tilde p = 1 - q $. Kupiec提出了原假设为$ p = \tilde p $的似然比检验，其中LR统计量：

q为VaR的分位数.检验结果如下所示(表 4).

从表 4中可以看出引入极值指标计算的VaR₂失败天数更少，失败率更小且更接近5%的概率设定，p值也表明引入极值指标计算的VaR₂能更准确度量风险，效果更好.

在对近7年上证综指收益序列数据的实证研究中，计算并比较未引入极值指标和引入极值指标两种情况下的风险值，检验样本证明引入极值指标计算风险值是更准确的风险测度.理论和实证均表明忽略序列数据自身相依性会导致风险被低估，而极值指标能够修正风险值，引入极值指标下的平稳序列的风险值更准确.