-
汽车电子节气门是当今汽车发动机能量管理系统中不可或缺的一环,发动机ECU根据加速踏板传感器信号、节气门位置传感器信号、进气温度信号等,通过设计微控制器,驱动电机获得不同工况下节气门的最佳开度.节气门控制的精度、反应的快慢以及抗干扰鲁棒性将直接影响发动机进气量和燃油喷射量,进而影响汽车的动力性和燃油经济性.
电子节气门具有非线性、不确定性、迟滞等特点[1-2],主要是电子节气门减速机构存在间隙,复位弹簧扭矩不连续,机械运动部件存在库伦、粘滞等多种摩擦.为了满足电子节气门动态过程快速、准确和稳态过程误差尽可能小的要求,国内外学者在电子节气门控制中做了很多研究[3-7]. Horn等[8]提出了一种超螺旋滑模控制算法,虽然能有效地消除电子节气门抖振,但由于在设计控制器时加入了模糊算法,使得系统实时控制运算变得复杂;张邦基等[9]提出了一种电子节气门位置最优预见控制算法,使节气门控制器对节气门物理参数难以辨别以及外部干扰不确定等因素的敏感度降低,以提高控制系统的稳定性和鲁棒性;郑太雄等[10]针对电子节气门的非线性特性,提出了一种基于Luenberger观测器的电子节气门全局快速滑模控制方法,并设计了扰动自适应律,较好地改善了电子节气门控制系统的稳定性和鲁棒性;Wang等[11]针对电子节气门的非线性迟滞特性,提出了一种基于前馈补偿器的智能模糊反馈控制算法,但用于补偿电子节气门迟滞特性的模糊规则设计得不够理想,以致于不能达到预期精确补偿电子节气门非线性迟滞的效果.孟志强等[12]针对电子节气门非线性问题,设计了一种非奇异快速终端滑模控制器,能有效地提高电子节气门系统的响应速度和控制精度.巩明德等[13]针对汽车电子节气门控制系统缺乏驾驶临场感、非线性以及未建模动态不确定性等问题,提出了一种双向伺服力反馈控制方法,以加强电子节气门控制系统的稳定性和鲁棒性.
本文针对电子节气门的非线性因素和外部干扰的复杂问题,分析了电子节气门的结构,提出了一种基于指数趋近律的滑模鲁棒控制策略,对电子节气门开度进行了高精度和快速响应控制,增强了电子节气门控制系统的鲁棒性和稳定性.
全文HTML
-
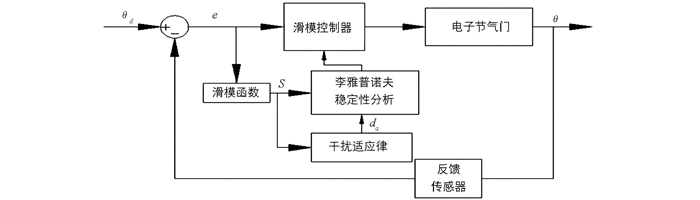
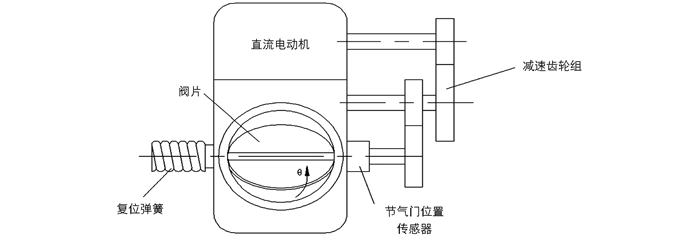
车用电子节气门主要由节气门阀、直流驱动电机、减速齿轮组、复位弹簧和节气门位置传感器等组成,电机输入电压在电枢回路中产生电枢电流,电枢电流与励磁磁通相互作用产生电磁转矩.电磁转矩克服节气门转轴上的负载,带动节气门转动,实现电子节气门转角位置控制,其结构如图 1所示.
根据基尔霍夫定律,直流电动机电枢电路方程为
式中,Ra为直流电动机的电阻(Ω);i为直流电动机电流(A);La为直流电动机的电感(mH);Vb为电动机反电动势(V);Ea为电动机输入电压(V);Kb为电动机反电动势常数(V/rad);θm为电动机旋转角度(rad);Tm为电动机转矩(N·m);KT为转矩常数(N·m/A).
将式(2)和式(3)带入式(1),得
根据牛顿第二定律建立节气门运动学方程
式中,Jt为电机侧系统总转动惯量(kg·m2);θ为节气门转角(rad);n为齿轮机构减速比(-);Tsp为复位弹簧扭矩(N·m);Tf为摩擦扭矩(N·m).
复位弹簧扭矩
式中,ksp为弹簧扭矩系数(N·m/rad);θ0为节气门初始角度(rad).
节气门摩擦扭矩
式中,kf1为粘滞摩擦系数(N·m/rad),kf2为库伦摩擦系数.
考虑到直流电动机的电感很小,取La=0,并忽略齿轮间隙的影响,所以直流电机转角θm与节气门转角θ存在以下关系
联立式(4)、式(5)、式(6)、式(7)、式(8),得电子节气门数学模型
因为电子节气门在工作时会受到复杂多变的外部干扰dt,所以定义电子节气门状态变量为x1=θ,
${x_2} = \dot \theta $ ,则电子节气门的状态方程为式中:
${a_1} =-\frac{{{K_b}{K_T}}}{{{R_a}{J_t}}}-\frac{{{k_{f1}}}}{{{J_t}{n^2}}}, {a_2} =-\frac{{{k_{sp}}}}{{{J_t}{n^2}}}, {a_3} = - \frac{{{k_{f2}}}}{{{J_t}{n^2}}}, b = \frac{{{K_T}}}{{{J_t}{R_a}n}}.$
-
本控制的目的是设计出使节气门快速、准确且稳定地到达目标开度的控制律.设θ为电子节气门实际开度,θd为电子节气门的期望目标开度,e为电子节气门跟踪误差变量,则
因此可定义滑模函数s为
式中,c为滑模参数,且c>0.
滑模函数s导数为
控制器采用指数趋近律,则
式中,ε>0,k>0.
联立式(10)、式(13)和式(14),得
则滑模控制律为
考虑外部不确定干扰dt,设计控制律为
式中,da为与干扰dt的界相关的实数.
将式(17)代入式(13),则
为保证电子节气门控制系统的稳定性,满足
式中,dL,dU为有界干扰.
定义Lyapunov函数为
控制律采用指数趋近律,则
为保证设计的电子节气门滑模控制系统是稳定的,应有
$\dot V < 0$ ,则使得取da=d2-d1sgn(s),其中,
因此滑模鲁棒控制律为
-
为了验证电子节气门滑模鲁棒控制器性能,首先在Matlab/Simulink中建立电子节气门模型,设计滑模控制器,并对节气门进行开度跟踪控制实验,电子节气门系统模型参数[14]如表 1所示.
根据式(9)、式(21)建立电子节气门仿真控制模型,如图 2所示.
本文以KL26单片机为微控制器搭建了基于指数趋近律的滑模鲁棒控制节气门模型.如图 3所示,主要包括KL26单片机、L298N双H桥直流电机驱动芯片、电子节气门以及电池.
本文选取的鲁棒滑模控制器参数如表 2所示.
PID控制器参数为
电子节气门轨迹跟踪平均绝对误差为
式中,N为采样个数.
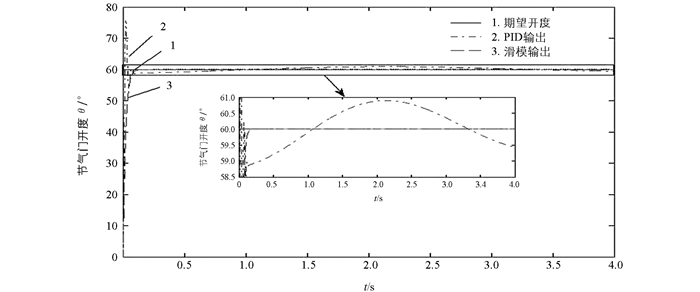
工况1:用阶跃信号模拟汽车在加速工况时的节气门变化,对阶跃信号跟踪性能进行分析.设电子节气门阶跃参考输入信号为θd=60°.
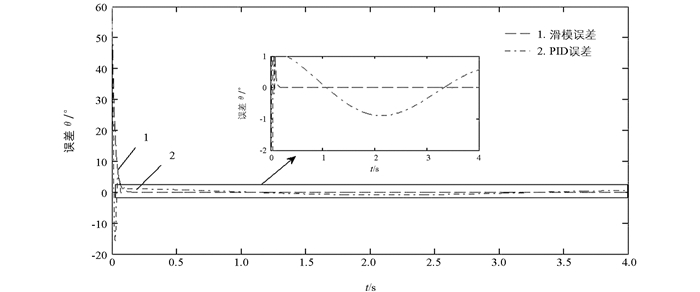
图 4与图 5分别表示电子节气门传统PID控制、基于指数趋近律的滑模鲁棒控制的跟踪响应曲线及误差曲线.由图 4可以看出,基于指数趋近律的滑模鲁棒控制能对期望开度进行有效的跟踪,其跟踪响应曲线没有超调量,而传统PID控制则有较大的超调量,达到稳态的时间比滑模鲁棒控制长.由图 5阶跃信号跟踪误差曲线及表 3可以看出,在响应达到稳态之后的仿真时间内,滑模鲁棒控制在控制精度上要优于传统PID控制.
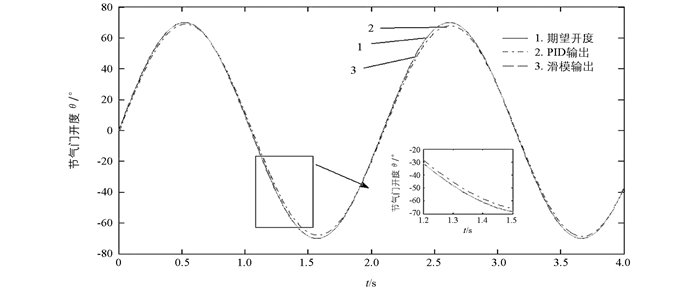
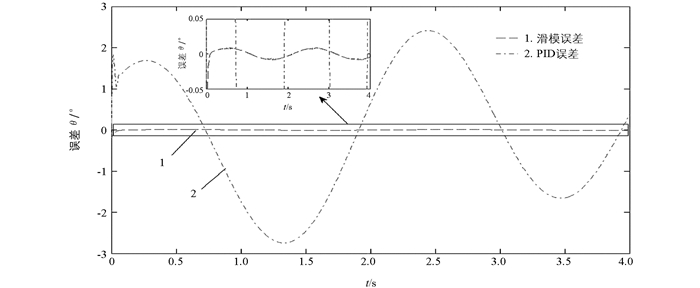
工况2:汽车运行工况复杂多变,可能出现连续加速、连续踩踏制动踏板减速或者加减速交替变化的情况,导致电子节气门的开度变化不确定.本文采用正弦输入信号模拟节气门开度变化,设电子节气门的参考输入信号曲线为θd=70·sin(t).
图 6为传统PID控制、基于指数趋近律的滑模鲁棒控制节气门跟踪响应曲线,图 7为传统PID与滑模控制的响应误差曲线,表 4为滑模鲁棒控制与传统PID控制误差对比表.从图 6、图 7和表 4可以看出,滑模鲁棒控制的实时响应性能比传统PID控制要好,且控制精度要远高于传统PID控制.
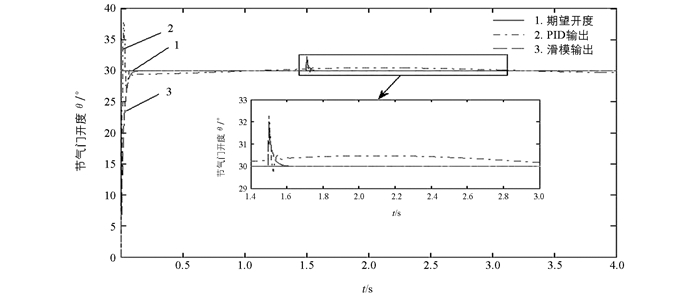
本研究同时进行了电子节气门的抗干扰控制实验.设电子节气门阶跃参考输入信号为θd=30°.在1.5 s时对电子节气门施加外部随机干扰,此时的电子节气门外部响应曲线如图 8所示.由图 8可以看出,基于指数趋近律的滑模鲁棒控制能在较短的时间内恢复到电子节气门的期望开度,其抵抗外部干扰的能力要优于传统PID控制.
从以上2种模拟工况可以看出,相较于传统PID控制,基于指数趋近律的滑模鲁棒控制器无论在阶跃还是正弦跟踪方面都可以做到快速响应,而且无超调现象,实现精准位置控制,对汽车不确定性工况变化也具有较强的鲁棒性,能够实现发动机节气门开度的高精度鲁棒控制,从而保证进气流量稳定精确控制,提高发动机的燃油经济性和汽车动力性.
-
本文针对电子节气门具有复杂性、非线性、时变性等问题,建立了电子节气门系统模型,设计了基于指数趋近律的滑模鲁棒控制器,改善了电子节气门系统的控制性能.与传统PID控制的对比实验结果表明,本文所设计的基于指数趋近律的滑模鲁棒控制能很好地满足电子节气门的控制要求,具有反应速度快,超调量小,稳态误差小,抗干扰能力强等特点,比较适应电子节气门的高性能控制.



 下载:
下载: