-
非线性现象在应用数学和物理中是一种常见的动力学行为,可以通过很多耦合偏微分方程来描述,如KdV-mKdV方程、KdV-ZK方程、KdV-Burger方程和耦合Schrödinger-KdV方程等[1].耦合Schrödinger-KdV方程是描述振动的电场和低频密度场扰动相互作用的物理过程.一般的耦合Schrödinger-KdV方程可表示为
设初始条件为N(x,0)=N0(x),E(x,0)=E0(x),x∈$\mathbb{R}$ ,t>0,ε>0为常数.方程(1)具有如下能量守恒特性:
其中I(0)为常数.
在计算机模拟过程中,设计尽可能保持微分方程能量守恒特性的数值格式对于精确地模拟微分方程的运动具有重要的意义[2].保持微分方程结构特性的数值算法已成为计算数学的一个重要部分. 1984年,在北京举办的国际微分方程与微分几何会议上,冯康院士作了题为“差分格式与辛几何”的报告,首次系统地提出了保辛结构的辛几何算法[3-5].后来Bridges和Reich等人在辛几何算法的基础上提出偏微分方程的多辛算法[6-7]. 1999年Quispel和McLachlan等人提出了二阶平均向量场方法,广泛应用于偏微分方程的计算[8-10],最近Celledoin等又提出了在时间方向上具有高阶精度的高阶保能量格式[11].
本文利用高阶平均向量场方法求解耦合Schrödinger-KdV方程.首先介绍高阶平均向量场方法,然后利用四阶平均向量场方法和傅里叶拟谱方法对耦合Schrödinger-KdV方程进行离散,从而得到其方程的高阶保能量格式,再对方程在不同初始条件下进行数值模拟,得出结论.
全文HTML
-
设u是关于(x,t)的函数,方程(1)可以转化成如下的无限维哈密尔顿系统
其中D是一个斜伴随算子
H[u]的变分可以表示为
将方程(2)在空间方向用拟谱方法或差分方法数值离散后可转化成有限维哈密尔顿系统
其中:S是斜对称矩阵,H(U)是哈密尔顿函数,U=[u0,u1,…,ui,…,uN-1],ui为u(x,t)在点xi的值.将高阶平均向量场方法应用于(3)式,可得
其中:Ui表示向量U的第i个分量,
$f_k^i = \frac{{\partial {f^i}}}{{\partial {x^k}}}$ ,${f^i} = \frac{{{\text{d}}{u_i}}}{{{\text{d}}t}}$ ,δij是克罗内克符号,α为常数.当α=0时,(4)式具有二阶精度;当$\alpha = - \frac{1}{{12}}$ ,$\mathit{\boldsymbol{\hat U}} = \frac{{{\mathit{\boldsymbol{U}}^n} + {\mathit{\boldsymbol{U}}^{n + 1}}}}{2}$ 时,(4)式具有四阶精度.方程(4)可写成矩阵向量的形式将(3)式中f(U)代入(5)式,可得到
在两边乘
再应用积分基本定理,可得到
从而有
由(6)式可知,四阶平均向量场格式(5)在时间层上能保持哈密尔顿系统(3)的能量守恒.
-
设E(x,t)=p(x,t)+q(x,t)i,耦合Schrödinger-KdV方程等价于
方程(7)可以表示成无限维哈密尔顿系统
其中:z=(p,N,q)′,
${\partial _x}$ 为一阶偏导数,相应的哈密尔顿函数为对无限维哈密尔顿系统(8)在空间方向用拟谱方法进行离散.
令xj(j=1,2,…,N1),tk(k=1,2,…,N2)为
$\left\lfloor {{x_0}, {x_{N1}}} \right\rfloor \times \left\lfloor {{t_0}, {t_{N2}}} \right\rfloor $ 内正规网格点.设Ω=[a,b],L=b-a.将Ω分为N等份,N为偶数,$\tau = \frac{L}{N}$ 是空间步长,则可以用xj=a+τj,j=0,1,…,N-1表示空间网格点.令pj,Nj,qj分别是p(x,t),N(x,t),q(x,t)在xj处的近似,定义为插值空间,其中gj(x)是满足gj(xi)=δij的正交三角多项式,gj(x)可表示成
其中:
对函数N(x,t)∈C0(Ω),定义插值算子IN为
对于插值算子,在配置点xj满足
由计算可得
同理可得
其中D1和D2分别是一阶谱矩阵和二阶谱矩阵,对于三阶偏导算子
$\partial $ xxx可用谱微分矩阵D1D2近似离散,从而可得到方程(1)的半离散拟谱格式其中:A=D1D2,di,j是矩阵D1第i行第j列的元素.方程(9)-(11)可写成有限维哈密尔顿系统
其中:Z=[PT,nT,QT]T,I是N×N单位矩阵,相应的哈密尔顿函数为
用四阶平均向量场方法离散(12)式,有
其中E,F,G,
${\mathit{\boldsymbol{\hat H}}}$ 分别为如下N×N阶对角矩阵故
方程(13)等价于
则(14)式可以写成
其中:i=1,2,…,N-1;
${{\hat d}_{i, j}}, {{\hat k}_{i, j}}, {{\hat i}_{i, j}}, {{\hat b}_{i, j}}, {{\hat a}_{i, j}}, {{\hat c}_{i, j}}, {{\hat f}_{i, j}}, {{\hat e}_{i, j}}, {{\hat g}_{i, j}}, $ 分别表示矩阵$\mathit{\boldsymbol{\hat D}}, \mathit{\boldsymbol{\hat K}}, \mathit{\boldsymbol{\hat I}}, \mathit{\boldsymbol{\hat B}}, \mathit{\boldsymbol{\hat A}}, \mathit{\boldsymbol{\hat C}}, \mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{\hat E}}, \mathit{\boldsymbol{\hat G}}$ 的第i行第j列元素.
1.1. 高阶平均向量场方法
1.2. 耦合Schrödinger-KdV方程的高阶保能量格式
-
为了验证格式保能量守恒特性,定义能量误差
其中
定义数值解与精确解的最大模误差为
收敛速度为
方程(1)具有精确解
-
取-150<x<150,ε=1,α=0. 45,
$\xi = {\left( {\frac{\alpha }{{10}}} \right)^{\frac{1}{2}}}x$ .文献[1]对二阶保能量格式的L∞误差做了分析.参照文献[1],表 1表示方程(1)中N在t=3时的二阶和高阶保能量格式的L∞误差和收敛阶,从表 1可以看出高阶保能量格式的精度明显高于二阶保能量格式的精度,并在时间方向上具有四阶精度.设方程(1)初始条件为
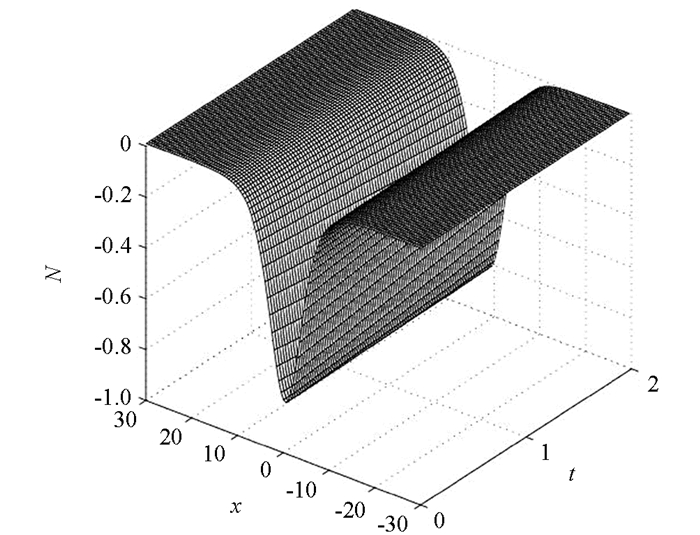
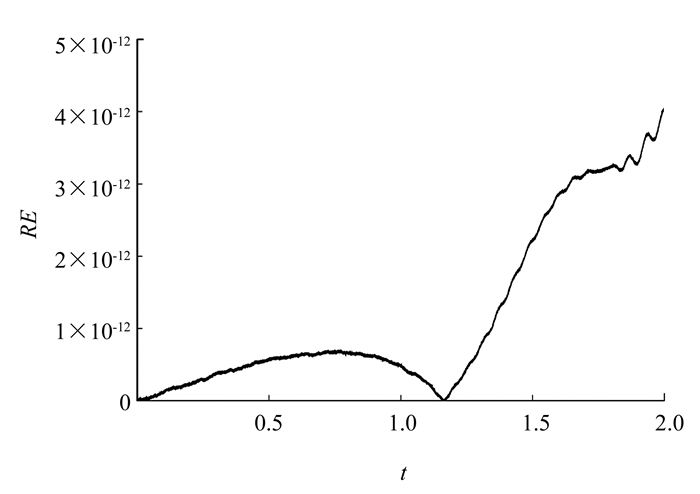
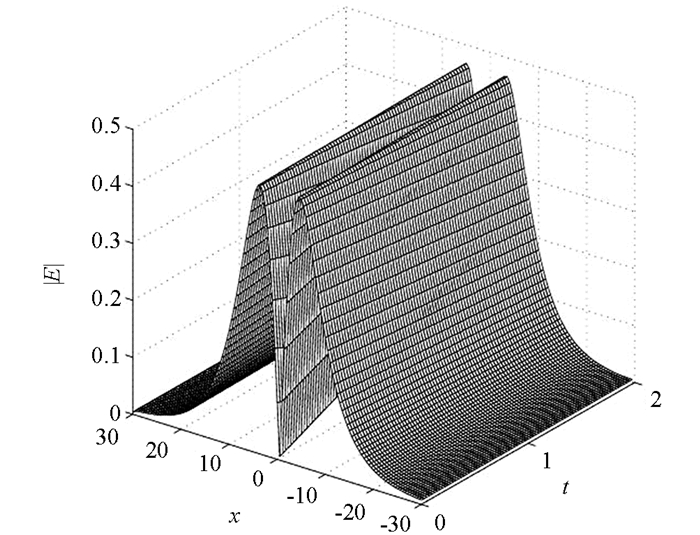
取x周期边界条件E(-30,t)=E(30,t),N=400,L=60,τ=0.005,dx=0.5. 图 1和图 2分别表示在t∈[0, 2]内解的演化行为,图 3表示方程(1)的能量误差随时间的变化,能量误差可忽略不计.高阶保能量方法能够有效地模拟方程孤立波的行为,并保持方程的能量守恒.
-
设方程(1)的初始条件为
其中:ξ=x,θ=γx,
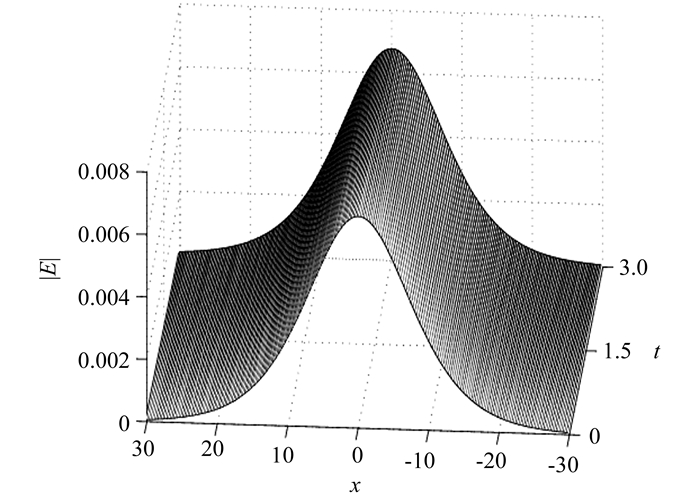
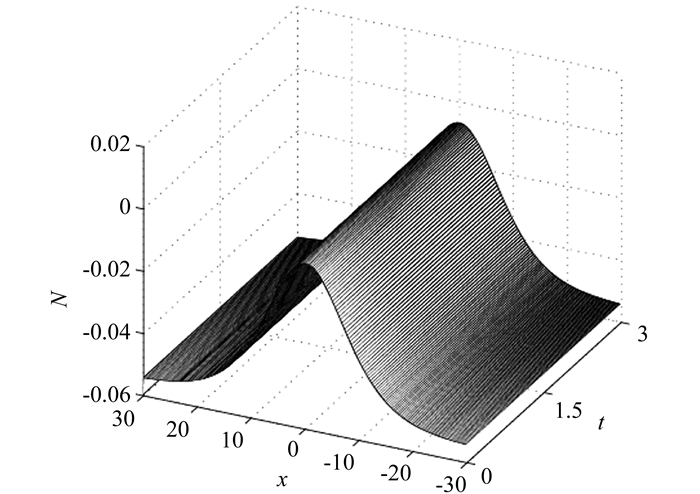
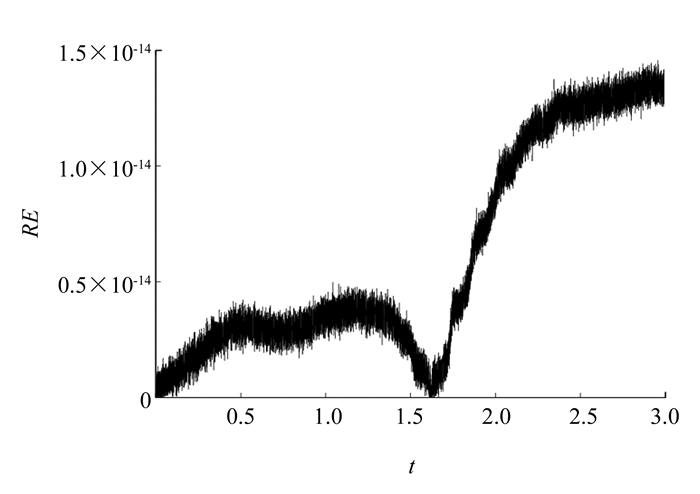
$\delta = \sqrt {\sqrt 2 {c_1}{c_3} + 4c_2^2} $ ,c1=c3=0,c2=0.01,γ=0.1,x周期边界条件E(-30,t)=E(30,t),取N=100,L=60,τ=0.01,dx=0.25. 图 4和图 5表示在t∈[0, 3]内解的演化行为,图 6表示能量误差随时间的变化过程,能量误差可忽略不计.同样可知,高阶保能量方法能够有效地模拟方程孤立波的演化行为,并保持方程的离散能量守恒.
2.1. 数值模拟1
2.2. 数值模拟2
-
本文用四阶平均向量场方法和傅里叶拟谱方法构造出耦合Schrödinger-KdV方程的高阶保能量格式,再通过在不同初值条件下数值模拟方程孤立波的行为并分析格式的保能量守恒特性得到新的高阶保能量格式.新格式能很好地模拟耦合Schrödinger-KdV方程孤立波的演化行为,并且可以精确地保持方程的离散能量特性,高阶平均向量场方法在数值模拟能量守恒特性的偏微分方程中具有显著的优势.



 下载:
下载: