-
许多自然科学现象和工程领域均涉及对流传热问题.对于给定流场的对流传热现象,其模型方程为对流扩散方程.由于传热介质结构的复杂性和实际问题中边界条件的多样性,我们一般无法得到对流传热问题的解析解,因此研究高效率、高精度数值求解对流扩散方程的新算法具有重要的应用价值.
对于对流扩散方程数值求解常见的差分格式有很多,如修正中心显示格式(CD)、迎风格式(FUD)、Crank-Nicolson格式(C-N)等,虽然都是绝对稳定的,但它们的截断误差均较低.目前已有许多研究对此进行了改进:文献[1-3]使用Hermite插值思路给出了求解空间的四阶差分格式,但只适用于稳态的对流扩散方程;文献[4-6]使用综合变换建立了求解对流扩散方程的一种两层四阶差分格式,但增加了离散方程节点数,计算比较复杂;文献[7]提出了求解一维定常对流扩散问题非均匀网格上的多项式型高阶紧致差分格式,但对于边界条件的处理较困难;文献[8]利用四阶精度的三次样条公式提出了时间二阶空间四阶精度的两层紧致隐格式;文献[9]提出了构造高阶精度的待定系数法,虽然很好地解决了对流项的耗散问题,但精度较低,且计算较复杂.
本文利用指数变换将对流扩散方程变为扩散方程,然后采用三点四阶紧致差分方法离散扩散方程的空间变量,利用扩展的
$ \frac{1}{3}$ -Simpson公式离散时间变量,构造出一种求解对流扩散方程的新的高精度紧致差分格式.
全文HTML
-
在计算流体力学中,天然河道中的水沙运动、水中污染物的扩散是最常见的一种流动现象,伴随着计算机技术的快速发展,建立数学模型已经成为模拟这些流动现象的一种重要手段,然而污染物的扩散和水沙运动数学模型可以写成统一的对流扩散方程形式,考虑如下简单形式的对流扩散方程
的初边值问题
其中:u(x,t)表示未知量,a为扩散系数,p为对流系数,Ω=[0, 1],d(x)是足够光滑的函数.
先做指数变换
将(2)式带入(1)式后可得
先对计算区域进行离散,空间方向进行N等分网格划分,步长
$h=\frac{1}{N} $ ,时间步长为τ,网格节点为(xj,tn),其中xj=jh,tn=nτ,j=0,1,2,…,N.对于任意固定的t,设vj(t)是v(xj,t)的近似值,(vxx)j(t)是vxx(xj,t)的近似值,(vt)j(t)是vt(xj,t)的近似值.对空间内部节点采用四阶紧致差分公式[10]来离散空间变量
其中δx2是二阶中心差分算子.将(4)式带入(3)式后可得到
其中:
采用扩展的
$ \frac{1}{3}$ -Simpson公式[11]对时间方向进行离散,设$\tilde v\left( t \right) $ 是v(t)的近似值,在区间$[{t_{n - 1}}, {\rm{ }}{t_n}] $ 上$\tilde v\left( t \right) $ 满足(5)式即其中
$\alpha = n - 1, \frac{{n - 1}}{2}, n $ ,则有其中
令(7)式中的s=1,
$\mathit{\boldsymbol{\tilde V}}\left( t \right) $ 在tn上满足(7)式,则有令(7)式中的s=12,
$\mathit{\boldsymbol{\tilde V}}\left( t \right) $ 在${t_{\frac{{n - 1}}{2}}} $ 上满足(7)式,则将(6)式带入(8)式和(9)式可得到
其中I为单位矩阵.
(10)式两边同时乘以
$ \left( {\mathit{\boldsymbol{I}} - \frac{\tau }{3}\mathit{\boldsymbol{C}}} \right)$ ,(11)式两边同时乘以$\left( {\frac{{2\tau }}{3}\mathit{\boldsymbol{C}}} \right) $ ,两者相加可得:通过文献[10]可知空间方向的离散具有四阶精度,通过文献[11]中的研究结果可知,时间方向也具有四阶精度,因此本文所构造的格式(12)的截断误差为O(τ4+h4).
-
引理1 对于矩阵A和B,假设λ和
$ \mathit{\boldsymbol{X}} \in {\mathbb{R}^{N - 1}}\left( {\mathit{\boldsymbol{X}} \ne 0} \right)$ 分别是矩阵A-1B的特征值和特征向量,则λ是实数且λ>0.证 由于λ和X分别是矩阵A-1B的特征值和特征向量,那么
令
那么
因为a>0,所以XTBX>0,同理XTAX>0,由λXTAX=XTBX
$ \Rightarrow $ λ>0且λ为实数.引理2 如果z>0,则有
证 当z>0时,有
由此,我们知
定理1 格式(12)是无条件稳定的.
证 假设λi(i=1,2,…)是矩阵C的任意特征值,则
$(12-6\tau {{\lambda }_{i}}+{{\tau }^{2}}\lambda _{i}^{2}){{(12+6\tau {{\lambda }_{i}}+{{\tau }^{2}}\lambda _{i}^{2})}^{-1}} $ 是$(12\mathit{\boldsymbol{I}}-6\tau \mathit{\boldsymbol{C}}+{{\tau }^{2}}{{\mathit{\boldsymbol{C}}}^{2}}){{(12\mathit{\boldsymbol{I}}+6\tau \mathit{\boldsymbol{C}}+{{\tau }^{2}}{{\mathit{\boldsymbol{C}}}^{2}})}^{-1}} $ 的特征值,根据引理1和引理2我们可以得矩阵C的特征值都为正的实数,且因此,式(12)是无条件稳定的.
-
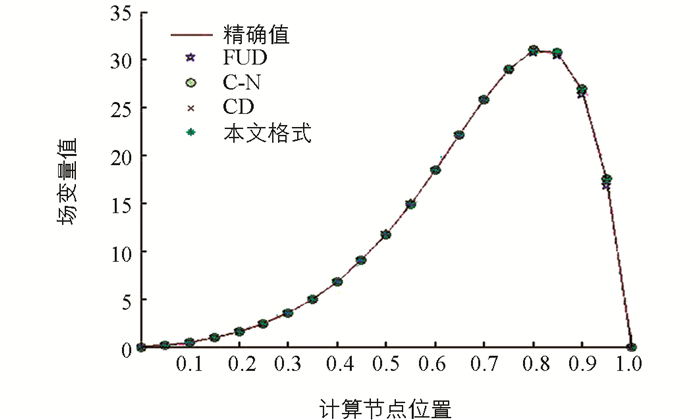
针对一维线性对流扩散方程提出了一种新的高精度紧致差分格式,其截断误差为O(τ4+h4),通过理论分析证明了该格式是无条件稳定的.通过数值算例将本文格式与FUD,CD,C-N格式的计算结果进行了比较,结果表明本文格式的计算结果精度较高.



 下载:
下载: