我们用$\mathbb{R}$^m和$\mathbb{R}$^m×m分别表示m维实向量集和m×m实矩阵集.本文出现的所有向量都是列向量.定义x_i(t)为智能体i在t时刻的估计.符号()^T定义为一个矩阵或向量的转置.对于一个矩阵A，a_ij为其第i行第j列的元素.定义1_m为元素全为1的m维列向量.符号I_m为m×m单位矩阵.我们用‖·‖表示一个矩阵或者向量的欧拉范数.定义向量e_i=[0，…，0，1_i，0，…，0]^T.一个非负矩阵A是行随机的如果A1_m=1_m成立，A是列随机的如果A^T1_m=1_m，A是双随机的如果A既是行随机又是列随机.给定一个任意、恰当、闭、凸函数f(x)，对任意的y∈$\mathbb{R}$^m，定义f^†(y)=sup_{x∈$\mathbb{R}$^m}y^Tx-f(x)为其共轭函数.

我们用G={V，E，A}表示一个非平衡有向加权网络，其中V={1，…，m}表示智能体集合，E⊆V×V表示边的集合；A=[a_ij]∈$\mathbb{R}$^m×m(a_ij≥0)表示网络G的加权邻接矩阵.具体地，如果(j，i)∈E，∀i，j∈V成立，那么它意味着智能体i可以直接接收从智能体j传来的信息，也就是a_ij＞0.用N_iⁱⁿ={j|(j，i)∈E}表示智能体i的入度邻居集合.有向网络中一条从智能体i₁到智能体i_k的路径可以表示为一系列有向连通边(i₁，i₂)，(i₂，i₃)，…，(i_k-1，i_k)，其中(i_j-1，i_j)∈E且j=2，…，k.在一个有向网络中如果智能体集中任意两个智能体之间总存在一条有向路径，则将这个有向网络称为强连通的.

总的来说，本文主要考虑如下分布式约束优化问题

∀i=1，…，m，其中x=[x₁，x₂，…，x_m]^T∈$\mathbb{R}$^m.每一个智能体i只可以获取自身的局部凸代价函数f_i：$\mathbb{R}$^m→$\mathbb{R}$.耦合线性约束集定义为M={x∈$\mathbb{R}$^m|$\sum\limits_{i=1}^{m}$ x_i=P}，不等式约束集定义为X={x∈$\mathbb{R}$^m|l_i^min≤x_i≤l_i^max}.假定X=X₁×X₂×…×X_m为X_i的笛卡儿积且S=M∩X表示优化问题(1)的可行解集.我们令x^*=[x₁^*，…，，x_m^*]^T，X^*和f(x^*)=f^*分别为优化问题(1)的最优解、最优解集和最优值.

优化问题(1)的拉格朗日函数L：X×$\mathbb{R}$→$\mathbb{R}$定义为如下形式

其中λ是等式约束$\sum\limits_{i=1}^{m}$ x_i-P=0的拉格朗日乘子.基于共轭函数的定义，对于一个给定的λ∈$\mathbb{R}$，优化问题(1)的对偶函数可以转化为如下形式

其中D_i(λ)=-f_i^†(-λ)-$\lambda \frac{P}{m}$是一个凹函数.因此，优化问题(1)的对偶问题可以表示为

其中D(λ)可能不可微.给定一个λ∈$\mathbb{R}$且假设(3)式中相应的最小值为$\mathit{\boldsymbol{\tilde x}}$，那么D(λ)的次梯度为

注意x^*为最优解.那么，由假设1可知，问题(4)必定存在一个对偶最优解λ^*满足强对偶性成立，即f(x^*)=D(λ^*).此外，一对最优解(x^*，λ^*)被称为拉格朗日函数L在集合S×$\mathbb{R}$上的鞍点，即

注意到根据(3)式求解(4)式等价于求解下列最小化问题

其中Q_i是一个凸代价函数

在假设1-3的基础上，我们提出了求解问题(7)的分布式优化算法.具体地，对于任意的t=0，1，…，我们用x_i(t)和λ_i(t)两个状态分别去估计原始最优解x_i^*和对偶最优解λ^*，用z_i(t)去消除网络的非平衡性.假设每个智能体i的初始值为x_i(0)∈X_i，λ_i(0)∈$\mathbb{R}$和z_i(0)=e_i∈$\mathbb{R}$^m.由此，变量x_i(t)，λ_i(t)和z_i(t)的更新规则如下

其中：α(t)是步长，z_i(t)=[z_i1(t)，…，z_im(t)]^T，▽Q_i(t)是函数Q_i(λ)在λ=$\sum_{j=1}^{m}$a_ijλ_j(t)上的次梯度.此外，我们有如下的假设.

假设1  非平衡有向网络G是强连通的.

假设2  对于任意的i=1，…，m，函数f_i是可微的且其次梯度▽f_i是利普希茨连续的，利普希茨系数为σ_i.也就是说，对于任意的y，x∈$\mathbb{R}$，▽f_i满足如下的不等式

假设3  权重矩阵A=[a_ij]∈$\mathbb{R}$^m×m是行随机的且其对角元素是正的.

假设4  步长α(t)是正的且满足sup_t≥0α(t)≤1，$\sum\limits_{t=0}^{\infty} \alpha(t)=\infty$和$\sum\limits_{t=0}^{\infty} \alpha^{2}(t) < \infty$.

注意到算法(11)是一个一致迭代过程，其最终迭代到矩阵A的一个左perron向量估计π=[π₁，…，π_m]^T满足1_m^Tπ=1.针对这个perron向量，我们有如下的两个引理.

引理1  让假设1和3成立，那么π是一个严格正向量且满足

引理1是Perron-Frobenius定理的一个主要结论.此外，引理1收敛速度是几何的.

引理2^[9]  设假设1和3成立，考虑到算法(10)和(11)，那么对任意的i，j∈V和t≥0，存在C＞0和γ∈(0，1)满足下面的不等式成立

其次，算法(10)可以转化为如下形式

其中

因此，我们有

其中用到条件‖▽Q_i(t)‖≤L，∀i∈V(根据假设2可知L存在).注意到z_ii(t)＞0，∀t≥0且

可以得到{z_ii^-1(t)}_t=0^∞是一个正有界序列.根据假设4，可以得到

由(15)式可知$\lim\limits_{t \rightarrow \infty}$ ‖ε(t)‖=0.定义λ(t)=$\sum\limits_{i=1}^{m} \pi_{i} \lambda_{i}(t)$.

由文献[9]易得如下引理3，4.

引理3  若假设1-4成立，根据算法(10)和(11)，可以得到下面条件成立

证  由上面分析可知，$\lim\limits_{t \rightarrow \infty}\|\varepsilon(t)\|=0$成立.因此，引理3的证明可以直接从文献[9]获得.

下面给出一个重要引理，这个引理对算法的收敛性分析起到了至关重要的作用.

引理4  若假设1-4成立，考虑算法(10)和(11)，那么存在γ∈(0，1)和t₀＞0满足对任意u∈$\mathbb{R}$和t≥t₀下面的不等式成立

其中

和

证  定义v_i(t)=∑_j=1^ma_ijλ_j(t).对任意的u∈$\mathbb{R}$，从算法(11)可以很容易得到

其中使用条件

和

得到(18)式. (18)式右边的第一项上界为

(18) 式右边的第二项的上界为

其中使用Q_i的凸性和次梯度有界性得到式(20).从(18)-(20)式可以得到

(21) 式两边同时乘以π_i然后在i求和得

其中π^TA=π^T.又因为

此外，

根据(22)-(24)式，可以很容易得到引理4的结果.

本文的第一个主要结果在下面的定理中指出.

定理1  若假设1-4成立，序列{x_i(t)}和{λ_i(t)}由算法(9)-(11)更新，可以推出$\lim\limits_{t \rightarrow \infty} \lambda_{i}(t)=\lambda^{*}$对任意i∈V都成立.

证  定理1的证明可以分为两部分.第一部分需要证明对偶状态的平均λ(t)随着t→∞渐进收敛到对偶最优解λ^*.根据引理3可知每个对偶状态λ_i(t)随着t→∞都渐进收敛到对偶状态的平均λ(t).因此，第二部分通过结合第一部分和引理3进而得定理1的结论.因为引理4得到的结论与文献[9]的定理1结论类似，所以可以参照文献[9]直观得到第一部分结论.因此，本文定理1的余下证明在这里省略.

接下来，给出本文的第二个主要结果.

定理2  若假设1-4成立，序列{x_i(t)}和{λ_i(t)}由算法(9)-(11)更新，可以推出$\lim\limits_{t \rightarrow \infty} x_{i}(t)=x_{i}^{*}$对任意i∈V都成立.

证  对于拉格朗日对偶问题(4)，可以推出至少存在一个对偶最优解λ^*和原问题(1)的唯一最优解x_i^*满足x_i^*=x_i(λ^*)对任意i∈V都成立.由定理1可知$\lim\limits_{t \rightarrow \infty} \lambda_{i}(t)=\lambda^{*}$对任意i∈V都成立.因此，由$\lim\limits_{t \rightarrow \infty} \lambda_{i}(t)=\lambda^{*}$可以得到每个原始状态x_i(t)都随着t→∞渐进收敛到一个唯一最优解x_i^*，也就是$\lim\limits_{t \rightarrow \infty}$x_i(t)=x_i^*对任意i∈V都成立.证明结束.

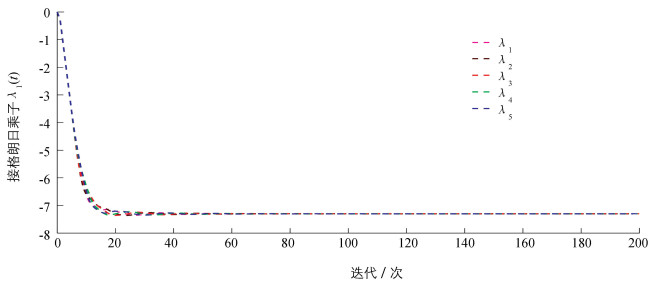
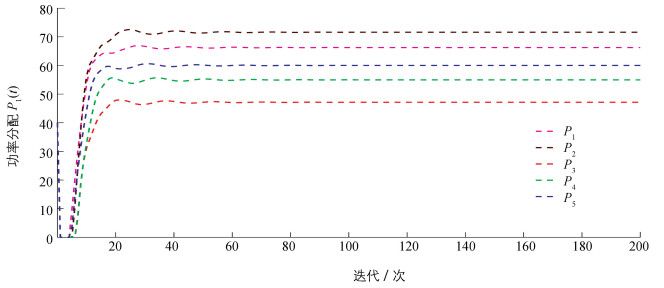
通过电力系统中分布式经济调度问题的仿真实例来验证所提出算法的有效性和分析过程的正确性.研究IEEE-14总线系统的经济调度问题，该总线系统结构可以参照文献[12].系统的通信结构由一个非平衡有向网络表示.在仿真中，假设每个发电机i存在其自身的代价函数Y_i(P_i)=a_iP_i+b_iP_i²，其中a_i和b_i是每个发电机i可调控的代价增益.考虑实际环境，不同发电机产生的功率可能不相同，因此所产生的功率都具有有限界限[0，P_i^max].假设每个发电机都知道系统总需求P=300 MW.最后，每个发电机参数a_i，b_i和P_i^max的取值参照文献[10].

基于以上的参数设计，算法(9)-(11)的仿真结果如图 1和图 2所示.从图中可以看出本文算法成功地为每个发电机分配最优功率，并且每个拉格朗日乘子收敛到对偶最优解.具体的最优功率分配为：P₁^*=66.24 MW，P₂^*=71.62 MW，P₃^*=47.15 MW，P₄^*=54.99 MW和P₅^*=60.00 MW；对偶最优解λ^*=-7.301.

本文开发并分析了一种完全分布式的原始-对偶算法，用于处理带有耦合线性约束和不等式约束的分布式经济分配问题.本文算法采用了行随机权重矩阵并且被证明是适用于非平衡有向网络.在代价函数是凸且利普希茨连续的假设下，所提出的算法渐进收敛到全局优化问题的精确最优解.此外，通过电力系统中分布式经济分配问题的仿真实例验证了算法的性能.在未来的研究中，将本文的工作扩展到智能体在时变非平衡有向网络上的事件触发，异步和量化通信的情况是非常有意义的.