-
作为人口大国,农业是关乎我国社会稳定的重要基础.近年来,我国在预防农业病虫害领域投入巨大,但是农业灾害,尤其是作物病虫害依旧屡见不鲜.频繁的虫害不但造成了难以挽回的经济损失[1],而且还导致了生态效益与社会效益下降.如果能够有效地对害虫发生趋势进行预测,就可以提前掌握虫害的发生动态,预防和采取相应的防治措施,更有效地控制灾害,进而减少虫害造成的损失.因此,能够准确地对虫害发生趋势进行预测预报,具有非常重要的意义.
现阶段,对害虫发生趋势预测的传统方法主要有期距预测、有效积温预测、多元线性回归预测及有效基数预测等[2].王淑芬等[3]研制了马尾松毛虫防治专家系统;王霓虹等人[4]基于Web GIS技术,研发了一款森林病虫害预测的专家系统.这类预测系统本质上都基于传统的专家系统.但是,我国幅员辽阔,气候地貌复杂,虫害的发生概率大小受到气候、天敌等众多因素的协同影响,不仅仅是简单的线性关系,而是一种复杂的非线性关系[5].同时,预测率较高的专家系统需要依赖于农业专家的人工预测,由于人工成本较高,普及率较低.
因此,寻求一种合理且更为准确的预测方法就显得尤为重要.本文提出一种以图像处理技术结合SVM机器学习的方法,通过这种方法,在不影响准确度的条件下,可以有效减少预测时的自变量数量,对虫害进行合理预测.
全文HTML
-
作为一种线性平滑去噪算法,采用高斯滤波算法,有算法成型快、容易实现的优点.由于绝大多数噪声可以近似为高斯分布的白噪声[6],因此本文采用低通高斯滤波器,过滤掉采集图像中的高斯白噪声,进而实现图像平滑.
根据选择的固定窗口大小及窗口内任意像素与中心像素点的距离,利用高斯函数实现系数权值的分配,即高斯滤波可以表示为
其中:Wx,y表示中心像素(x,y)的M×M(M为奇数)大小的领域;ωd为空间距离相似度权重因子,即图像中任意2个像素之间的空间距离比例,距离越小,权重越大.根据图 1,各个昆虫距离明显分布不均匀,若单纯为了计算权重,则误差较大.为了方便程序实现和减小误差,进行单位化,区间为[0, 1],图 1对应的ωd为0.78.
由公式(1)可知,在低频区间,高斯滤波算法有良好的处理效果,但其仅仅考虑了像素间的边界关系,而忽略了整体图像区域可能存在拟合特征[7],由于采用固定的掩模窗口,对于该图像区域进行求和取平均值实现归一化,可能导致丢失平滑区域中的细节信息,所以本文通过高斯滤波,对图像区域内的不同领域像素设置了不同权值,在保证图像可以平滑的同时,能够更多地保留图像总体灰度分布特征.同时,本文采用的是提取数学形态特征,对于纹理、触角等传统特征没有进行提取,细节信息丢失对于特征的提取影响不大.
图 1左边部分是采集的原始图像,右边部分是进行高斯滤波后的原始图像(图片采集:诱虫灯大田拍照),去除了原始图像中的高斯白噪声.
-
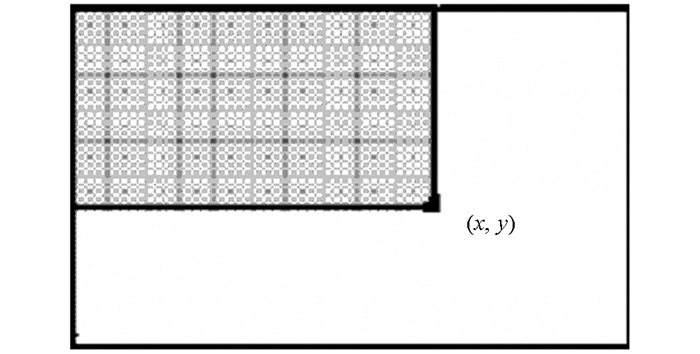
将图像中任何一点(x,y)处的积分图像表示为它左上角的所有像素的总和:
其中,ii(x,y)表示积分图像也称Harr特征;i(x,y)表示原始图像;如图 2所示,点(x,y)处的积分图像为灰色区域的像素和[8].
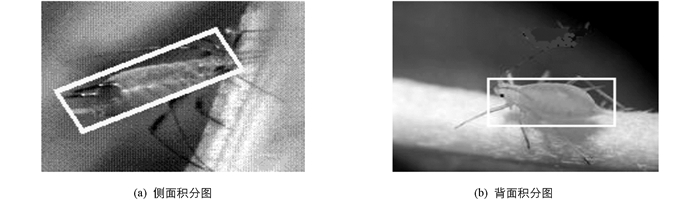
事实上,大多数昆虫在农田里都是运动状态,或可观察的视角角度并非水平或垂直,拍摄过程中难以保证昆虫以固定角度出现,所以本文特征的提取来源,主要是水平或侧面角度随机进行拍摄的图片.以蚜虫为例见图 3,不同角度拍摄的Harr特征.
-
昆虫的特征很多,比如颜色、斑纹、大小体长、体宽等[9].识别精度与选取的特征值有着密切的关系,但是并非所有特征值都对识别精度有促进作用.事实上,存在部分特征值对于识别精度有降低的效果,因此我们需要淘汰一些不适用的特征,进行特征值筛选过滤.尝试在特征向量中去除一个特征值xi,j,将剩下的特征向量构成样本采集合用于Jackknife检测[10],得到Aj和Bj.通过检测每个Harr特征的互补特征向量,得到一组对于整体特征向量集合的影响特征向量A0和B0.
图 4中有部分特征值未识别,原因是该类型昆虫体积过小,也符合实际的工程情况.
SVM的特点是适合两元分类,对于小部分比较浅或者不规则的成虫数据遗失影响不大,很适合做小样本监督学习.
其中,图 4中图片总像素S=6 250,通过各个昆虫大小累加去和值
$ K = \sum\limits_{i = 1}^n {{k_i}} $ ,得到图 4中昆虫图像部分像素的累计面积.虫口密度δ为
其中,S为图 4图像部分的像素总值,K为图 4图像中的昆虫累计面积,φ为比例系数,比例系数根据季节随之改变.这里实验采用的是0.25.
2.1. 特征提取
2.2. 特征分类
-
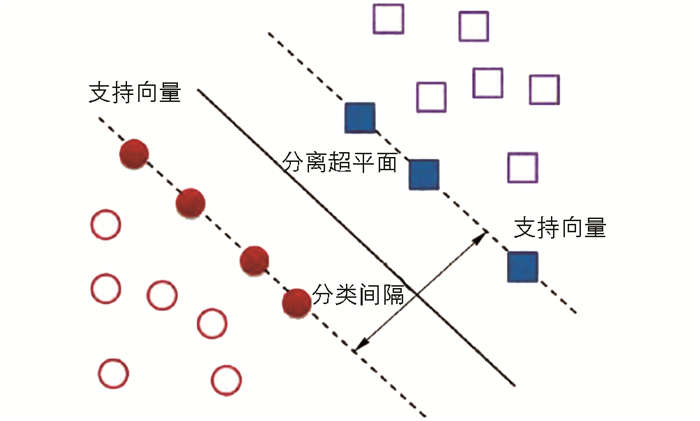
支持向量机(Support Vector Machine,SVM)由训练和核函数组成,基于有限的样本信息,对样本数据进行分类,在线性可分二元分类中,所有的数据点都在二维平面上,所以此时分割超平面就只是一条直线.但是,如果给定的数据集是三维的,此时用来分割数据的就是一个平面,该平面为最优超平面.
支持向量机就是离分割平面最近的那些点,是支持向量积的基本原理[11-14].其中,最大化支持向量到分割面的距离,就是支持向量机的目标.最优超平面可以提高模型的预测能力和减少错误分类.图 5展示了什么是最优超平面,用“红色”代表的样本类型1,“蓝色”代表样本类型-1.
根据图 4提取的特征,得到了图 4昆虫的图像特征值,见表 1.
SVM可以很好地应用于函数拟合问题,本文采用支持向量机,根据表 1特征值的类型,设置回归函数的参数,可求得回归式
其中,Ti和Ti*为拉格朗日乘子;xi为待预测因子向量;x为支持向量的样本子向量;b为偏置量.
对非线性问题,要用核函数方法将原始数据映照到高维特征空间,使其转化为线性问题求解,可求得回归式
其中:K(xi,x)为支持向量的核函数.
近年来,SVM这类机器学习算法在实际应用中越来越普及.余秀丽等[15]利用SVM模型对小麦叶部病害进行识别,结果表明SVM模型的预测识别准确率较高,并且模型算法实现较容易,误差低,对于小麦叶部的病虫害识别成功率有提升效果.向昌盛等[16]、夏永泉等[17]利用SVM模型对黏虫的病害发生量进行预测,认为该模型可以有效提高病虫害发生的预测精度,对于病虫害发生概率事件,这类规模较小且非线性的样本预测比较适合.基于前人的研究成果,本文也选取了SVM模型进行建模预测.
-
一个模型的数据一般分为训练集和测试集,训练集用于模型的自我学习,进行规律的总结;测试集用于验收模型经过训练后的成型效果.一般来说,训练集占总体数据集比例为75%~85%,测试集为15%~25%,本研究中随机选取了1992,1998,2000,2006,2011,2013的数据作为测试集(表 2),1980-2016年中剩余年份可以作为训练集(由中国气象局国家气候中心和人地系统主题数据库提供,可根据年限地区筛选自由选择).
根据公式(5)建立模型.将核函数K(xi,x)的参数定义为4个,x1为当年7-8月平均最低气温;x2为当年1月降水量;x3为当年7-9月份平均气温之和;x4为对应年份特征提取后的虫口密度.其中,x4=δ,计算过程将图像处理中的单一虫口密度逐条累加,再根据公式(3)计算.
根据归一法,b趋近于0,由于变量多,本文SVM采用的是多项式内积核函数
其中,g,c,d为参数,d为变量个数,即核函数的变量个数为4,可根据数据集的有效数据类型数量进行改变;g为时期参数,对于昆虫而言,成虫、幼虫时期在同一采集面积下的虫口密度肯定不一样,本文由于设备和条件有限,采集病害昆虫都为成虫期.本文筛选的病虫成虫期的体积大概是该类虫害幼虫期体积的10~14倍,为了方便统计,将虫害的成虫和幼虫图像大小体积显示比设置为10:1,这里g选择为10;c为区间(0,1)的一个常数,当该值减小时,对应的直线斜率会减小.建立模型,模型相关系数α如表 2所示.
为保证预测结果直观且有连续性,本文将模型的参考时间序列的长短设置为至少5个连续样本.在预测第i个样本时,后续样本不会参与模型的训练;在预测第i+1个样本时,再将第i个样本进行模型的训练预测.采用Python建立SVM模型,并以均方根误差(Root mean square error,RMSE)作为指标来衡量多元线性回归,进行SVM性能比对. RMSE定义为
其中,Xobs,i为实际值;Xmodel,i为预测值;n为预测样本数.表 3为部分实验数据展示.
本文样本数据来源:1980-2016年全国各地区小麦病穗率数据,实际值可以从中国气象局国家气候中心进行查询对比.
-
通过Pycharm软件,通过选取样本建立SVM模型,再利用6组测试样本对建立的SVM模型进行测试,预测结果和实际结果对比见表 4.
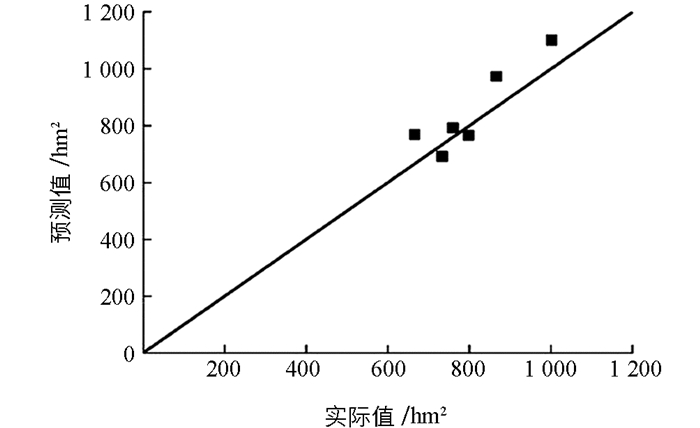
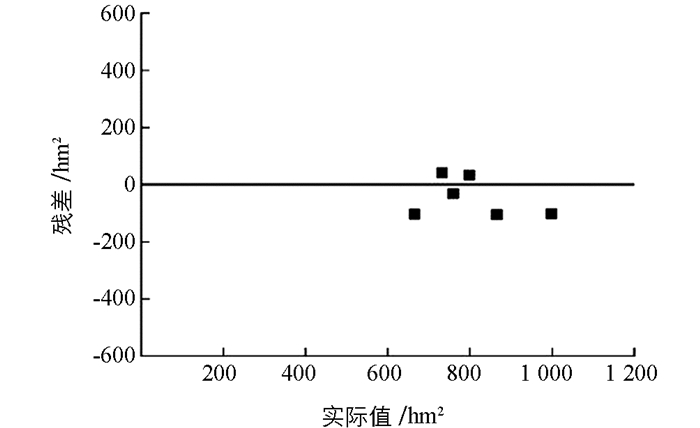
根据表 4可知:SVM的RMSE为72,SVM模型对6组测试样本都达到了准确预测,通过公式(8)计算平均误差为10%,即预测准确率为90%.该模型的预测结果可用图 6中的点来表示,线性直线表示实际的虫害面积,图 6表明SVM预测结果与6组测试样本中的实际虫害面积均较为接近.根据图 7、图 8可以看出,SVM所描绘的点均围绕残差等于零的直线上下随机散布,说明SVM模型对虫害面积预测有较好的效果.
3.1. 支持向量机简介
3.2. 建模方法
3.3. SVM预测结果
-
通过实验不难发现,图像处理可以得到害虫的部分特征,而对这部分特征合理地筛选、计算可以得到相应的数据. SVM模型适合处理小样本问题,分类预测的精度较高.
相比于传统的病虫害发生面积预测方法,本研究利用图像处理和SVM减少了传统预测方法中复杂的人工预测部分.通过利用有限的自变量进行病虫害预测,节约预测时间,节约人力成本,比较符合实际工程上的需求.预测结果显示预测准确性高,科学有效,证明了本文方法的优越性.




 下载:
下载: