-
图像边缘可定义为图像中出现亮度、灰度突变区域的所有像素的集合,图像边缘中隐藏着大量有价值的特征信息,能准确反映出物体的形态特征[1-2],进一步提取可获得多种有效参数.目前,图像边缘检测可应用于很多领域中,例如,图像配准[3-4]、图像分割[5]、模式识别、计算机视觉等[6].电力机房三维建模场景中,边缘信息可以更好地将物体和背景区分开,使得电力机房中的各种通信设备和二次电力设备等物体的三维重建更加准确.
图像边缘检测发展经历了两个阶段,传统的图像边缘检测算法以Canny算子、Prewitt算子、Log算子和Laplace算子为主要检测算法.王贵彬[7]提出了一种改进的Canny算子和抗噪形态学算法融合的边缘检测算法,改进后的Canny算子在一定程度上保持了图像的边缘强度及细节,同时很好地降低了噪声的影响.传统图像边缘检测算子的计算过程相对来说更简单、易实现、实时性好,但是获取边缘定位精度不高、连续性差、对噪声非常敏感,在噪声污染的情况下使用效果差[8].针对传统方法的缺点,涌现出大量的改进算法,其中基于小波变换的图像边缘检测算法得到了广泛的应用,刑尚英[9]结合小波模极大值和基于贝叶斯风险估计的小波域去噪,通过仿真实验证明该方法较之传统的小波算法有更好的图像边缘检测效果.张涛[10]研究了小波变换模极大值边缘检测方法,并结合全向小波变换、形态学以及Hausdorrf距离的知识提出了新的边缘检测算法,在准确检测边缘的同时新算法还能抑制部分噪声,为人们提供较清晰的边缘信息.但是该方法存在提取结果连续性差、适应性不足的缺点[11].
随着数学形态学在图像处理领域的应用,已形成了完备的形态学理论[12-14],目前该理论在图像去噪、边缘检测、区域分割等二值和灰度图像处理领域中被广泛应用.本文采用小波变换[15-17]和多尺度多结构的方法分别对低频图像和高频图像进行处理,提取图像的边缘信息,再进行融合叠加.实验结果表明,此方法可有效抗噪、保证边缘连续性、保留更多的图像纹理信息且定位准确.
全文HTML
-
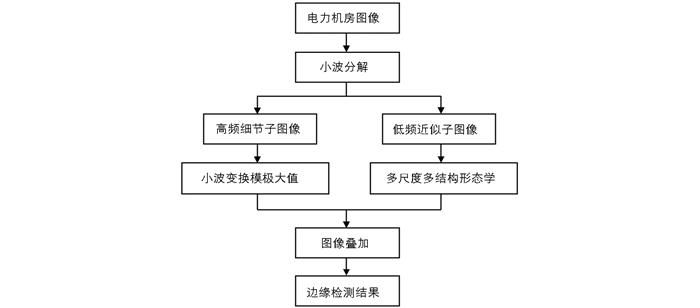
本文提出的这种融合小波变换模极大值和多尺度多结构形态学的图像边缘检测方法具体操作流程如图 1所示.
-
现定义光滑二元函数θ(x,y),它满足以下公式:
不同尺度s上的高斯平滑函数θs(x,y)与图像f(x,y)作卷积,则
其中,公式(3)中s=2j,s表示小波变换尺度因子,在尺度s下二维子波表示为
在尺度s下,经高斯平滑函数θs(x,y)处理图像f(x,y),可得到小波变换的2个分量,
公式(6)中wsxf(x,y), wsyf(x,y)分别是f(x,y)沿着水平方向和垂直方向的梯度矢量,即边缘信息.那么,模值、梯度方向可分别表示为下列公式(7)(8):
因此,对小波系数取局部模极大值便可得到图像边缘信息,极大值点的集合就是最终图像的边缘.
-
数学形态学方法的运算对象主要是二值图像,它主要包括4种运算规则,膨胀、腐蚀、开启和闭合.基于数学形态学方法检测图像边缘是利用结构元素对图像进行操作后,再根据一定的数学关系与原始图像运算得到图像边缘.
膨胀运算利用结构元素对图像进行扩大或填充,可以让图像中的裂缝等得到填补.膨胀运算如公式(9)所示:
腐蚀运算利用结构元素消除图像中比结构元素小的成分,可以收缩图像,消除物体边界点.腐蚀运算如公式(10)所示:
公式(9),(10)中F(x,y)为灰度图像,B(s,t)为结构元素.膨胀运算和腐蚀运算互为对偶.开启运算、闭合运算是基于膨胀运算和腐蚀运算的混合操作.开启运算是先腐蚀后膨胀,它可以用来消除小物体,扩大较小间隙;闭合运算是先膨胀后腐蚀,它可以消除狭窄的间断,可平滑边界.开启运算和闭合运算互为对偶.开启运算如公式(11)所示,闭合运算如公式(12)所示.
上述两式中⊗表示腐蚀运算,⊕表示膨胀运算.由腐蚀、膨胀、开启和闭合进行混合运算,可得到3种经典的边缘检测算子如公式(13),(14),(15)所示:
以上这些基本的形态学检测算子在噪声和边缘信号上难以共同兼顾,式(14)可保留更加完整的图像边缘信号,但是噪声信息会被增强,无法很好地去噪,式(15)可以较好地忽略噪声,但是对图像边缘信息的提取不完整,边缘信号较弱.
-
针对基本形态学检测算子在噪声和边缘信号上表现的不足,为获得边缘连续、精确的检测结果,本文采用一种多尺度多结构形态学检测算子.若采用单一结构算子很难检测出形状不同的边缘信息;若采用单一大尺度算子能快速去噪,但是会忽略尺度小的图像细节,无法保证边缘提取的完整性;若采用单一小尺度算子可提高边缘提取的精确性,但是噪声会难以去除,降低提取效率.本文采用以下算子进行处理:
其中,F是灰度值图像,B1,B2,CI是不同尺度不同结构的元素,通过式(16)不同结构元素处理后的EI(F),由式(17)运算合成边缘信息.本文选取的B1,B2是半径为3的正方形和圆形结构元素,CI的选取如下所示:
-
图像叠加是将小波变换模极大值提取的高频近似图像的边缘信息和多尺度多方向结构元素形态学提取的低频近似图像的边缘信息进行叠加,获得最终原始图像的完整边缘信息. Ih(i,j)为高频子图像边缘信息,Il(i,j)为低频子图像边缘信息,叠加后的图像边缘信息为I(i,j):
其中,α,β为加权因子,满足两者之和为1,α,β分别反映了高频子图像边缘信息和低频子图像边缘信息在叠加后图像边缘信息中的比例.
1.1. 图像边缘检测方法总流程
1.2. 小波变换模极大值
1.3. 数学形态学
1.4. 多尺度多结构形态学
1.5. 图像叠加方法
-
为验证本文提出的边缘检测算法在电力机房图像边缘信息提取中的有效性,在Windows 10、Matlab 2016a上对多种边缘检测算法进行模拟仿真实验,电力机房原图见图 2,不同方法检测到的原始图像边缘信息如图 3-图 6所示. 图 3-图 6分别展示了小波变换模极大值算法、数学形态学算法、多尺度多结构数学形态学算法以及本文算法对原始图像的边缘检测结果.
从图 3展示的仿真结果可知,小波变换模极大值算法有一定的抗噪性,边缘信息虽然相对清晰但是不连续;由图 4可知数学形态学算法提取的边缘信息更加连续,然而噪声信息太多,去噪效果太差;在图 5中,多尺度多结构数学形态学算法在抗噪、边缘信息的连续性上相对图 3和图 4都表现较好,但是定位效果不好.对比图 5、图 6易知图 5中一些边缘信息不够直观清晰,其定位精度不如图 6.综合以上对比可知,本文算法同时兼顾了抗噪性能、边缘连续性和定位效果,证明本文提出算法的有效性.
-
本文在前人的研究基础上,融合小波变换模极大值算法和多尺度多结构数学形态学算法各自的优势,提出了一种新的图像边缘检测算法用于电力机房图像边缘提取.仿真实验结果表明,与小波变换模极大值算法、数学形态学算法、多尺度多结构数学形态学算法相比,本文算法在抗噪性能、边缘连续性、定位精度上综合实力最强,不仅可以保证提取的电力机房图像边缘信息清晰、完整,还能保留更多的纹理信息,并且定位精确.但是,本文仍然存在几个可进一步完善的地方:图像叠加过程中应当充分考虑图像的特征再决定不同边缘检测方法的边缘结果所占的比例;针对不同的场景图像边缘检测应用,可根据图像特点选择合适尺度和结构元素的形态学算子.



 下载:
下载:




