-
开放科学(资源服务)标志码(OSID):

-
青藏高原独特、多变的气象特征是气象学的热点研究领域. 针对青藏高原及其周边复杂地形下的大气结构和地—气物理交换过程等方面的研究已获得了丰硕的成果,然而广袤的高原却由于地面气象观测站分布较少且极端天气、自然灾害等客观原因,很多观测站数据存在缺、漏等现象,无法提供丰富的实时观测有效数据. 因此如何提高观测数据质量,用少量的不连续的观测数据修补缺失数据是基础数据研究领域非常重要的科学问题. 本文基于严重不足的气象数据,采用POD(proper orthogonal decomposition,本征正交分解)优化后形成的Gappy POD算法与模式相结合的方式重构了近地面水平风速.
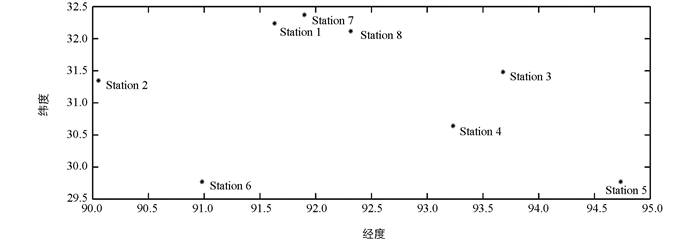
本文研究区域(图 1)为中国西藏那曲地区中东部一带,平均海拔超过4 500 m,具有典型的复杂高山地形特色. 该区域常年大风天气,且由于地形原因风场呈现复杂结构以及高度空间变异性特点[1]. 这些因素使得中尺度模型[2]的计算变得极具挑战性. 除去地形复杂的特点之外,该广袤区域内气象观测站较少且分布极度稀疏,导致数据分析的经典方法和基于大气运动方程的数值算法无法对气象要素进行高精度预测或重构. 本文采用模式与观测数据相结合的思路,利用美国国家大气研究中心(national center for atmospheric research,NCAR)的中尺度WRF(weather research and forecast)模式[3-5]计算了研究区域内格点数据并以此为基础进一步计算了区域内宏观风场特征以及风速特征;本文建立的Gappy POD算法的主要优势在于实现了利用局部观测数据调整宏观气象特征所存在的系统误差从而重构所得气象要素,兼具宏观大气运动规律和局部观测数据精度高的特点.
全文HTML
-
若研究区域内缺失数据较为严重则一般空间插值或外推方法无法较好地处理缺失值问题或重构问题. 比如POD是一种用于提取离散数据特征信息的降维技术,而缺失值较多时该方法在一定程度上失效. 本文通过优化原经典L2范数达到弥补POD方法在缺失数据下的不足. 为了提高气象要素场的重构精度,本文在研究区域内利用WRF模式[6]计算了相应气象要素在所有格点处的输出值从而建立了风速场的POD基,即代表该区域的宏观气象特征. 观测数据在本文中视为真值(近似为零误差). 利用观测数据矫正POD基的精准度,从而反演区域内任意一点处的气象要素值. 文中所采用的思想属于如今很多科学家提倡的“弱机理”思想范畴,即模型与数据结合的研究模式[7],体现宏观大气运动规律与局地观测数据的较好结合,因此该方法在很大程度上优于纯粹的数据挖掘技术(无机理)或纯粹的基于物理规律的技术(强机理).
-
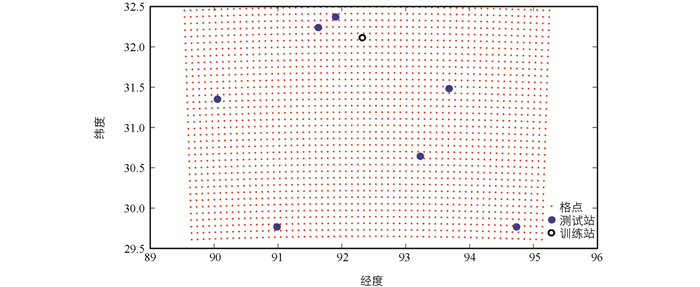
本文的研究区域分布着8个较稳定的地面气象观测站,分别为安多、班戈、比如、嘉黎、林芝、纳木错、那曲和聂荣站. 本论文采用交叉检验(cross-validation)的方法,将7个观测站的数据用于训练算法,剩下1个观测站选为测试站. 本文采用2014年8月8日02:00至2014年8月29日02:00期间近地面层10 m逐半小时水平风数据,因此每个观测站共有312个连续的观测数据值. 8个观测站分布在研究区域内3 km等间距分布的2 160个网格点之间,具体格点与训练观测站以及测试观测站分布如图 2所示. 本文采用的方法适用于观测站与网格点位置的任意分布情况.
-
WRF模式是一种中尺度天气预报模式,其先进的数据同化技术、功能强大的嵌套能力和先进的物理过程使得它适用范围广泛. WRF模式反映大气的物理运动规律. 而由于地形和气象现象的复杂性,WRF模式在区域性和中小尺度的模式输出方面通常具有较高的系统偏差. 本文将充分利用观测数据、模式输出和算法相结合的方式,确保重构数据既满足大气运动规律又同时具有局部测量数据的特征.
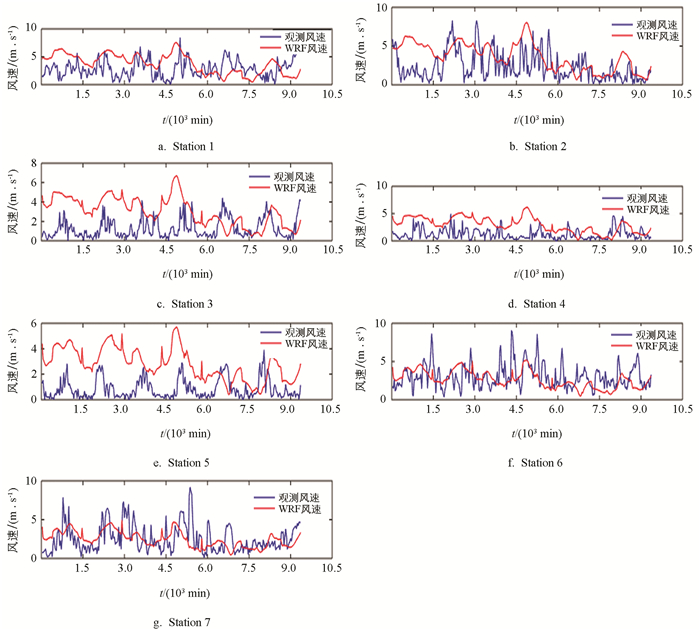
WRF模式计算所用的初始数据为美国国家环境预报中心2014年的实时gft风数据并且参考了文献[8]中针对青藏高原设计的WRF物理参数. 在本文中设置了两层嵌套网格,每层均设置36*60个网格点,内外层网格格距分别为3 km和9 km. WRF模式输出值WRFout为离地面10 m高风场纬向分量U10和径向分量V10,输出值间的时间间隔为30 min. 图 3显示WRF运算所得风速值在大部分时间点处高于实际观测风速值,因此该现象可理解为WRF系统性误差.
1.1. 观测数据
1.2. WRF模式
-
在观测数据严重缺失时经典POD方法往往由于无法求解L2范数从而失效. Gappy POD的主要思想为通过建立面具阵(mask matrix),将求解L2最小值的问题降纬至已有数据的纬度从而将原问题转化为低纬度上的L2范数最值问题.
-
文中d1,d2,d3分别表示网格点数、训练所用站点数和检验测试所用站点数,且相应数值分别为d1=2 160,d2=7,d3=1.
定义
$\widetilde{\boldsymbol{U}}, \widetilde{\boldsymbol{V}} \in \mathbb{R}^{d \times N}$ (其中d=d1+d2+d3=2 168表示空间点,N=1 008表示时间点),表示WRF模式计算所得所有空间点(包括网格点和观测站)的水平风速值:其中:每一列uj,vj∈
$\mathbb{R}$ d,j=1,…,N;d=d1+d2+d3表示每半个小时的数据集;每一行表示每个空间点在不同时间点的模式水平风场数据.$\widetilde{\boldsymbol{U}}, \widetilde{\boldsymbol{V}} \in \mathbb{R}^{d \times N}$ 矩阵的前d1行表示网格点处的风场数据,d1+1到d1+d2行表示7个训练观测站点处的风场数据,最后一行对应第8个观测站处的风场数据,且该站点位置和数据将用于测试和检验以及评价该方法的有效性.为了推导方便,将训练集和测试集分别写成如下形式:
令
$\underline{\boldsymbol{U}}=\left(u_{d_{3}, 1}, \cdots, u_{d_{3}, j}, \cdots, u_{d_{3}, N}\right)$ 和$\underline{\boldsymbol{V}}=\left(v_{d_{3}, 1}, \cdots, v_{d_{3}, j}, \cdots, v_{d_{3}, N}\right)$ ,其中(U,V)和(U,V)分别表示训练集和测试集,因此$\widetilde{\boldsymbol{U}}=\left(\begin{array}{l} \boldsymbol{U} \\ \underline{\boldsymbol{U}} \end{array}\right), \widetilde{\boldsymbol{V}}=\left(\begin{array}{l} \boldsymbol{V} \\ \underline{\boldsymbol{V}} \end{array}\right)$ . -
令
$\dot{\boldsymbol{u}}_{j}, \dot{\boldsymbol{v}}_{j} \in \mathbb{R}^{\left(d_{1}+d_{2}\right)}$ 与$\dot{\boldsymbol{U}}, \dot{\boldsymbol{V}} \in \mathbb{R}^{\left(d_{1}+d_{2}\right) \times N}$ 为样本的中心平均值. 文中为了简化符号,分别用uj,vj,U,V代替$\dot{u}_{j}, \dot{v}_{j}, \dot{U}, \dot{V}$ 且$\boldsymbol{\varLambda}^{u}, \boldsymbol{\varLambda}^{v} \in \mathbb{R}^{\left(d_{1}+d_{2}\right) \times\left(d_{1}+d_{2}\right)}$ 和Wu,Wv表示对应协方差矩阵UTU,VTV∈$\mathbb{R}$ (d1+d2)×(d1+d2)的特征值和特征向量. 按照特征值的大小顺序对特征向量进行排序,选取前q个主特征向量Wqu,Wqv∈$\mathbb{R}$ (d1+d2)×q,则POD基可定义为如下形式:假设
${\mathop {\boldsymbol{u}}\limits^{^\circ }}_{j}, {\mathop {\boldsymbol{v}}\limits^{^\circ }}_{j} \in \mathbb{R}^{\left(d_{1}+d_{2}\right)}$ ,j=1,2,…,N. 为7个训练观测站的观测数据集,则问题转化为求解如下最值问题:由于
${\mathop {\boldsymbol{u}}\limits^{^\circ }}_{j}, {\mathop {\boldsymbol{v}}\limits^{^\circ }}_{j}$ 仅代表观测数据,其中对应于Uqaj,Vqbj的格点数据缺失,导致(4)式中各项的数据纬度出现严重差异. -
令矩阵P∈
$\mathbb{R}$ d2×(d1+d2)具有如下形式,其中:O为d2×d1的零矩阵;I为d2×d2的单位阵. 矩阵P能够使d2×(d1×d2)纬度问题降至d2×d2纬度,即d2×d1纬度信息被面具形式隐藏,因此该P矩阵取名为面具阵. 将该面具阵作用于原最小值问题,从而得
(6) 式中各项维度均为d2×d2,因此该问题转化为经典最小值求解问题. 针对存在缺失数据的POD问题,Gappy POD算法[9-16]可通过面具阵将模型中存在缺失数据的项移除(隐藏). 经简易推导可求得上述问题解的表达式如下:
-
本文结合7个训练观测站数据以及研究区域内WRFout格点数据,通过Gappy POD算法重构了研究区域内任意点处离地10 m的水平风场数据,取得了较好的效果.
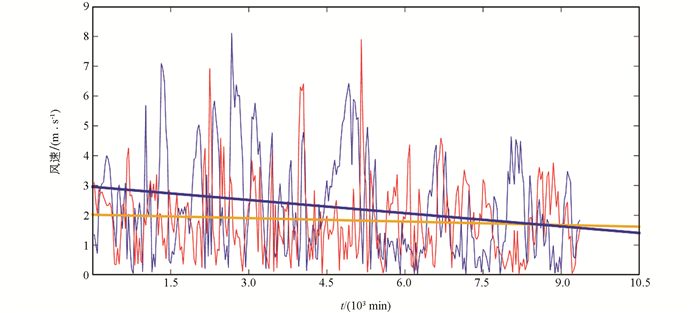
首先,经比较可知,测试站点处单独采用WRF模式计算所得风速平均误差为2.262 1,而经过Gappy POD方法进行风速重构后平均误差可降至1.838 4(如图 4所示,其中蓝色曲线表示WRF模式在测试站点处的风速重构误差,红色曲线表示采用Gappy POD后在测试站点处风速重构的误差,两条直线分别为对应颜色曲线的线性拟合),因此当观测数据质量较差时,如某些站点观测数据与真实情况相差较大以及站点的数据在某些时间段存在缺失等现象时,Gappy POD方法可用于提升观测质量.
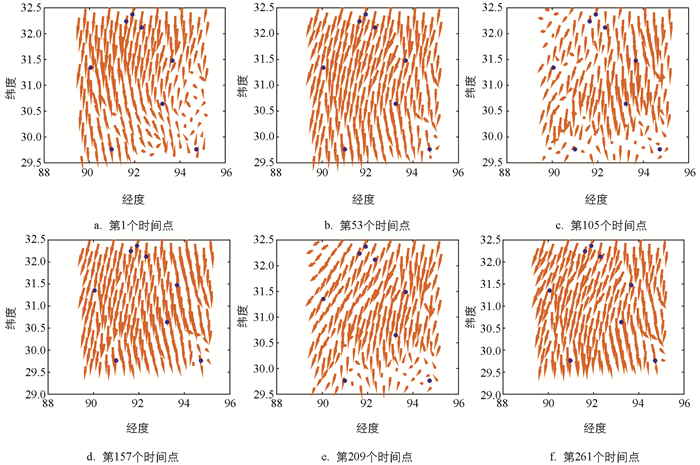
其次,Gappy POD方法可应用于提取气象要素的宏观特征. 图 5展示了采用Gappy POD算法在26 h内的6个时间点所重构的所有网格点处的水平风场. 由于网格点个数远大于观测站点的个数,因此所重构的每个格点处的数据精度有待进一步提升. 然而该方法不同于数据同化,可以在采用较低计算成本的基础上对气象要素在研究区域内的整体特征提供一定的参考信息.
最后,本文方法可用于重构研究区域内的任意点作为的预测点,均能取得较好的重构效果. 比如,在那曲市偏僻山区处建设信号基站时,可采用本文方法重构候选点处的高精度风速数据.
2.1. 数据分割
2.2. POD基的建立
2.3. 面具阵(mask matrix)的建立
2.4. 风速重构效果检验和风场重构
-
本文通过研究西藏那曲一带地形复杂和观测站分布稀疏区域的风速重构问题,介绍了流体力学领域处理缺失值问题的Gappy POD方法,并且将该方法应用于风速重构问题. 文中采用Gappy POD算法将模式与观测数据结合的方式提升了模式的重构精度. 本文介绍的方法在处理小尺度且数据量小的气象要素重构问题时具有精度高、易于操作以及计算成本低的特点,并且文中介绍的方法可以应用于解决其他气象要素的缺失值处理和重构问题. 本文也展示了采用该方法重构所有格点处水平风场数据的结果,然而数据同化并非本文研究的目的和文中方法的主要特点,因此采用该方法重构所有格点数据的结论仅在认识研究区域内气象要素宏观特征时做为参考.



 下载:
下载: