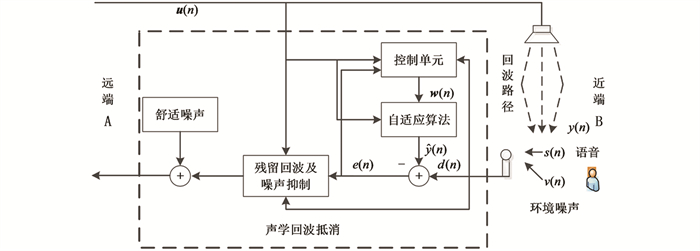
本文基于图 1所示的声学回声消除系统框图进行分析^[13]，回声消除的主要任务是避免远端用户A在与近端讲话人B通话时听到自己的回声. 系统在近端B应用回声消除模块，该模块包含控制单元、自适应算法和残余回波抑制. 为进一步提高语音质量，还会添加适当的舒适噪声来提升用户的听觉感受. 整个过程除需保持良好的全双工特性外，还需避免因为声学路径突变导致系统发散，同时还要尽可能地减少计算复杂度，保证算法的可移植性.

远端用户A发出语音信号u(n)=[u₀(n)，u₁(n)，…，u_L-1(n)]，将语音信号送入扬声器播放出来，经过未知的回波路径w^o=[w₀^o(n)，w₁^o(n)，…，w_L-1^o(n)]后，得到回声信号y(n)=u^T(n)*w^o(n)，L表示回声路径长度，加上背景噪声v(n)，背景噪声和回声信号一起被话筒拾取，得到期望信号d(n)=y(n)+v(n). 假定背景噪声符合零均值、方差为σ²的高斯分布. 回声消除的核心就是利用最小均方算法求出w来对回声路径建模，然后估计出回声信号，并与期望信号d(n)相减得到误差信号e(n)=d(n)-u^T(n)*w(n). 根据文献[14]，基于低阶混合范数的块稀疏最小均方算法代价函数表示为：

此代价函数是关于抽头系数的二次凸函数，因此必然有全局唯一最小值，λ是一个正数因子，‖w‖_2，0是改善回声信道的块稀疏特性所施加的零吸引力，‖·‖_2，0表示矢量的低阶混合范数l_(2，0)，n是回声消除器阶数的分组数. 额外的惩罚因子l_(2，0)范数条件约束改善了算法的稀疏性能.

为进一步改善算法在复杂声学环境中的鲁棒性能，本文利用基于鲁棒统计学思想的最大似然估计代替原本的最小均方误差准则，提出了鲁棒型块稀疏归一化最小均方算法(Robust Block Sparse-Normalization Least Mean Square，R-BS-NLMS)，该算法将代价函数修正为：

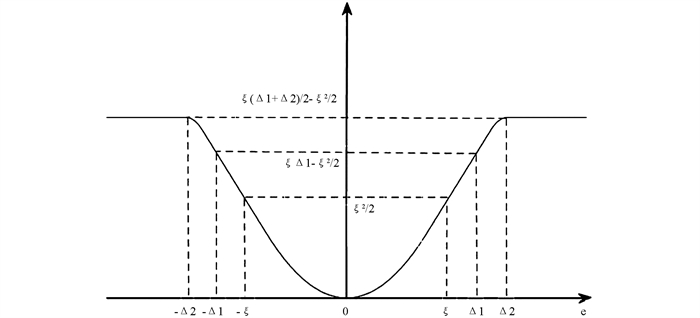
式(2)的ρ[e(n)]不再是传统的均方误差函数，而是为了抑制冲激噪声的M-估计，本文选取了式(3)所示的Hampel三段下降函数. 如图 2所示的Hampel三段函数是一个非线性有界函数，将其作为代价函数可以有效地抑制冲激噪声对权系数迭代的影响，保证算法在冲激干扰下依旧保持收敛性. 因此，本文提出算法将BS-NLMS中均方代价函数的推导改写为M-估计，将代价函数重新改写. 参数ξ，Δ1和Δ2是控制冲激噪声压缩幅度的门限参数，当冲激噪声幅度超过给定门限T_h时，ρ[e(n)]函数会抑制误差e的值，ξ，Δ1和Δ2的值越小，抑制干扰的能力越强，这3个参数的值需要结合中值滤波进行在线自适应估计，具体的估值选取将在后面参数估计时给出.

利用负梯度最陡下降法，将修正后的代价函数进一步对滤波器权矢量w(n)求导，得到式(4)新的权系数更新公式：

式(4)中，$\boldsymbol{g}(\boldsymbol{w})=\left[g_1(\boldsymbol{w}), g_2(\boldsymbol{w}), \cdots, g_L(\boldsymbol{w})\right]^{\mathrm{T}} $，g_j(w)在0＜$ \|\boldsymbol{w}[\lceil j / p\rceil]\|$≤1/α定义为g_j(w) $\triangleq $ $ 2 \alpha^2 w_j-\frac{2 \alpha w_j}{\| \boldsymbol{w}[\lceil j / p\rceil]\|}$，其他时值为0，α是一个正常数，P是滤波器系数的分组长度，式(4)中μ是用于调整稳态误差和收敛速度平衡的步长参数，ε是归一化处理中防止除零操作的小正常数，γ=μλ/2，q(e(n))是ρ[e(n)]关于w的一阶偏导，由式(2)可以看出，当非高斯噪声导致误差信号大幅度增加时，ρ[e(n)]的取值在相对平缓的最后一段，权系数的增加量接近于零，算法迭代几乎停止，所以基本消除了非高斯噪声对算法性能的影响，而回声抑制能力不受影响. 式(4)中的步长衡量因子$ \mu q(e(n)) / \boldsymbol{u}(n) \boldsymbol{u}^{\mathrm{T}}(n)+\varepsilon$满足文献[15]中提出的抗冲激干扰条件. 步长调节因子在冲激噪声发生时自动调节步长，消除权重矢量由于大幅度误差信号引起的更新可能性. 当瞬时误差较小时，此算法性能趋于均方误差自适应算法. 因此，该算法在复杂的声学环境中仍然保持较好的回声抑制能力.

本文涉及较多参数，包括门限参数ξ，Δ1和Δ2，步长参数μ在高斯白噪声和冲激噪声干扰下的取值范围.

门限参数ξ，Δ1和Δ2可以通过下面的方法求得. 首先假定估计误差e(n)是满足零均值的高斯分布，然后叠加加性冲激噪声，通过估算误差e(n)中不含脉冲噪声部分的方差值，观测并去除e(n)中的脉冲噪声，误差|e(n)|比给定门限T_h值大的概率为^[16]：

式(5)中，${erfc}(x)=(2 / \sqrt{\pi}) \int_x^{\infty} e^{-x^2} d x $是互补误差函数，$\hat{\delta}_e(n) $是随机冲激噪声的估计标准差，

分别代表误差e(n)大于ξ，Δ1和Δ2的概率密度函数，通过恰当地选取θ_ξ，θ_Δ1和θ_Δ2的值，可以得到ξ，Δ1和Δ2的值. 为了估算门限参数的值，需要对$ \hat{\delta}_e(n)$进行自适应估计：

式(7)中med(·)代表中值滤波，c₁=1.483(1+5/(N_w-1))是有限样本校正因子，N_w是估计窗长，λ_e是遗忘因子，A_e(n)={e²(n)，…，e²(n-N_w+1)}. $\xi=\kappa \hat{\delta}_e(n) $，κ是常数，控制对冲激噪声的抑制程度，同理可得门限参数Δ1和Δ2.

步长μ的取值指冲激噪声下算法能够稳态收敛的范围，也即回波路径权系数不断逼近维纳-霍夫解w₀=R^-1P的过程. 具体范围可由如下步骤求得，首先利用混合高斯模型对噪声进行数学建模^[13]：

式(8)中，v_im(n)=b(n)v_w(n)是冲激噪声，b(n)服从离散概率分布为P_r(b(n)=1)=P_r和P_r(b(n)=0)=1-P_r的伯努利随机序列，v_g(n)和v_w(n)是满足零均值、方差分别为σ_g²和σ_w²的高斯白噪声，随机过程的方差σ_v²=σ_g²+σ_im²=σ_g²+P_rσ_w²，当b(n)取0和1时，方差分别为σ_g²和$\sigma_{\Sigma}^2=\sigma_g^2+\sigma_w^2 $，最终得到混合高斯模型对噪声建模的概率分布函数为：

定义每个迭代时刻的失调量c(n)=w_o-w(n)，w_o是最佳权系数，在进行具体分析前需要假设输入信号，滤波器权重系数向量和噪声三者是统计独立的，且输入语音信号是一个自相关矩阵为R = $ E\left[\boldsymbol{u}(n) \boldsymbol{u}^{\mathrm{T}}(n)\right]$，服从零均值高斯分布的遍历过程. 基于以上假设，结合式(4)推导出全新的权系数更新公式，算法写为：

对式(10)等式两边求数学期望，可得：

E[·]表示对{v(n)，c(n)，u(n)}共同求取期望值，H=E_{{v(n)，c(n)，u(n)}}[μq(e(n))e(n)u^T(n)/u(n)u^T(n)+ε)-γg]，采用文献[17-18]中的推导方法，将式(11)进行一系列变量代换^[19]和一阶有限差分方程的求解后，可以得出步长取值范围为：

冲激噪声发生时，根据式(8)、式(9)的建模，将式(12)中σ_g²改写为(1-P_r)σ_g² +P_rσ_Σ²，得到新的步长取值范围为0＜μ＜2/(L+2)[(1-P_r)σ_g² +P_rσ_Σ²].

为了验证改进算法的性能，比较改进算法与BS-NLMS算法的回声抑制性能，本文设计了两个实验来对比，在仿真实验过程中采用归一化均方偏差(Normalized Mean Square Deviation，NMSD)作为衡量算法回声抑制能力的指标，即算法跟踪曲线，其定义为：

归一化均方偏差包括稳态误差和收敛速度. 稳态误差越小，代表回声抑制效果越好；而收敛速度代表算法需要经过多长时间达到理想效果.

实验1零均值高斯随机信号通过一阶自回归(Auto Regressive，AR)模型产生输入信号，高斯白噪声的输出信噪比设定为SNR=30 dB，冲激噪声幅度和频率分别为r_im=100，P_r=0.005，幅度表达式为r_im=p_rσ_w²/σ_g²，遗忘因子λ_e和λ_p都设置为0.99，中值滤波窗长为14. 为避免偶然性实验结果，所有实验仿真曲线都是100次独立实验求平均值获得.

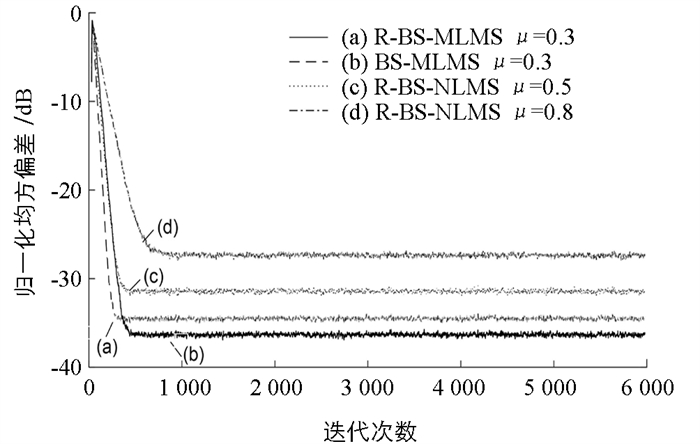
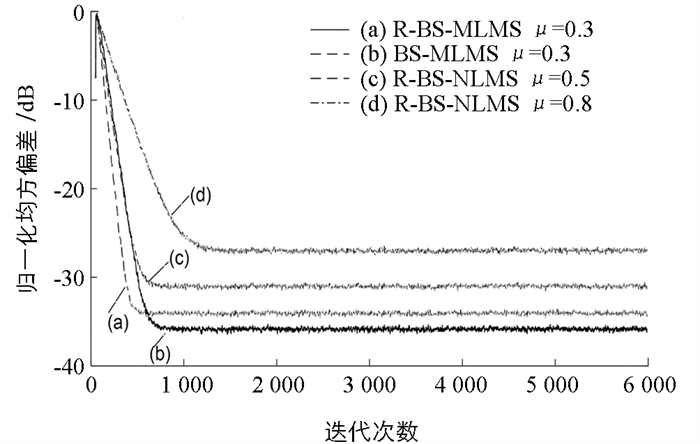
R-BS-NLMS算法在不同步长下的NMSD性能比较如图 3所示. 图 3以AR(0.7)模型作为输入信号，滤波器长度选择32，考虑到现实情况中多以长滤波为主，图 4给出了滤波器长度为128时的算法性能曲线. 由图 3、图 4可以看出，滤波器长度增加后，跟踪性能并没有降低.

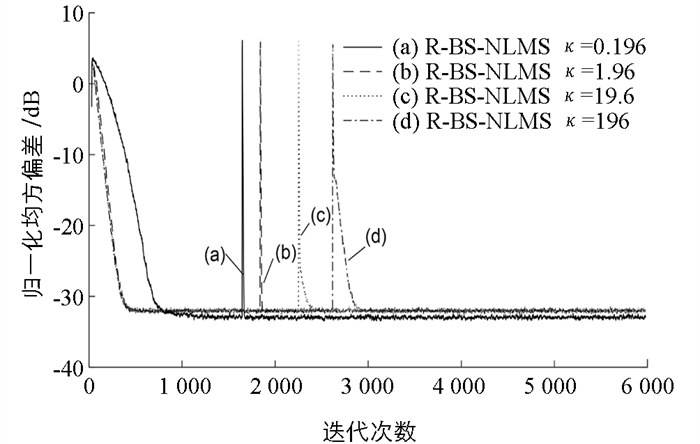
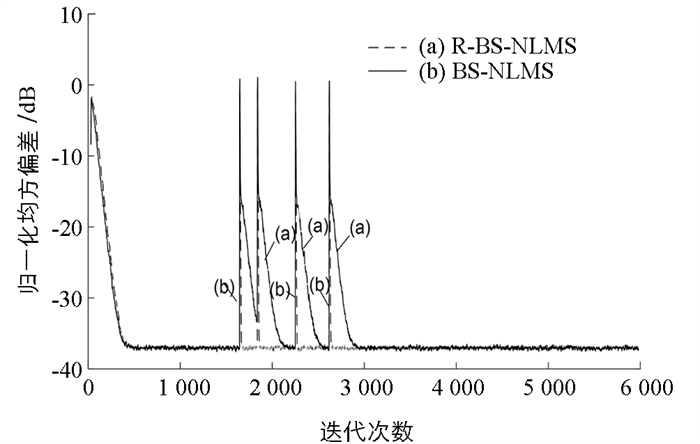
图 5验证不同的噪声抑制参数κ对算法回声抑制性能的影响，以选取出最优值，并将结果运用于后面的实验. 为了更清楚地看出噪声对期望信号的影响，将环境突发脉冲噪声的位置固定在迭代次数为1 648，1 841，2 253和2 620的地方. 在冲激噪声下R-BS-NLMS算法中参数κ在不同取值条件下算法收敛及跟踪性能曲线如图 5所示，参数κ用于控制算法受脉冲干扰的抑制程度，通过获得的最优参数可以确定门限参数. 从图 5中可知，随着参数值κ不断增大，算法逐步呈现出发散状态，且值越大发散程度越严重. 当κ选择较小的值时，算法面对冲激噪声均保持稳态收敛，但是当选择的数值过小时，算法收敛速度会受到抑制，如图 5当κ选择0.196时，收敛速度明显变慢. 综合考虑收敛速度和发散程度，本文认为1.96是最好的选择，并将结果进一步运用到下一个仿真对比实验当中.

R-BS-NLMS算法和对比算法BS-NLMS的NMSD跟踪性能曲线比较如图 6所示，两个算法都在经过大约400次迭代后达到了稳定状态，块稀疏最小均方算法在语音回声消除这样具有块稀疏特性的环境中常常遇到冲激噪声. 本仿真实验中将冲激噪声的发生固定在特定位置，第一次冲激噪声出现在迭代次数为1 648的位置，BS-NLMS算法在冲激噪声下会立刻呈现出发散状态，且需要重新经过数百次迭代才能收敛；而R-BS-NLMS算法则几乎不受冲激噪声的影响，并没有出现发散的情况，在迭代次数为1 841，2 253和2 620处也得到了相似的结果，主要原因是改进算法的权系数更新公式在冲激噪声发生时自动调节步长，消除掉权重矢量由于大幅度误差信号引起的更新可能，因此R-BS-NLMS算法具有良好的鲁棒性.

为进一步验证本文所提R-BS-NLMS算法的性能，实验2采用真实语音信号进行声学回声消除实验. 该实验在长、宽、高为4.35 m，3.2 m，2.8 m的房间进行音频数据采集，房间配置了普通家具家电，扬声器和麦克风分别摆放在电脑两侧，且两者距离0.45 m. 电脑摆放在中间负责数据处理，麦克风录制远端语音信号，经过房间的回声信道形成回声后被麦克风拾取，同时被拾取的还有近端信号和环境噪声. 根据房间真实脉冲响应设置滤波器截断长度L=1 024，音频数据采样率为8 000 Hz.

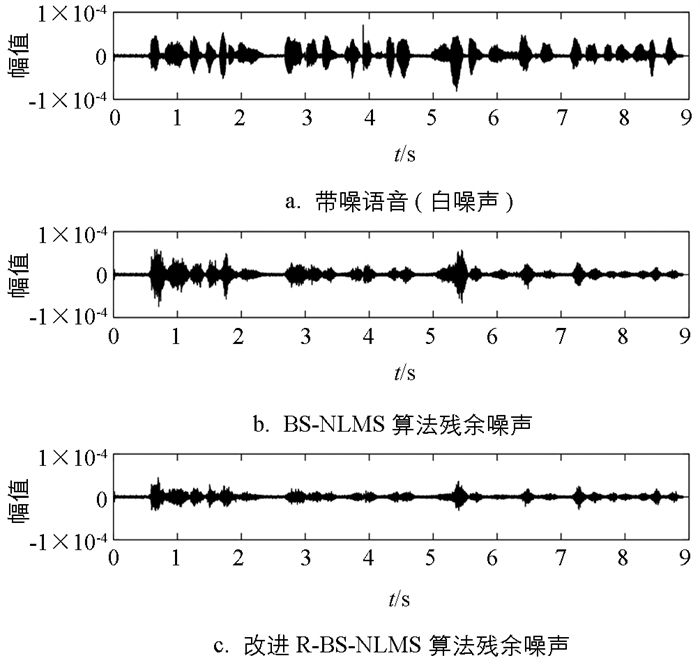
图 7为带噪的语音信号波形图，噪声源采用NOISEX-92数据库中的数据进行测试，语音信号具有在10~30 ms范围内的准稳态特性及高相关性，不考虑双端讲话情况. 图 7a是加入高斯噪声的时域波形图. 从图 7b和图 7c中可以清晰看出，与图 7a相比，两种算法的回声都被大幅度地消除掉，特别是在幅值较大的区域. 在听感方面，无论对于BS-NLMS算法还是本文所提的R-BS-NLMS算法，回声抑制效果都很明显，但是本文所提的R-BS-NLMS算法消除回声更多，回声抑制效果稍好.

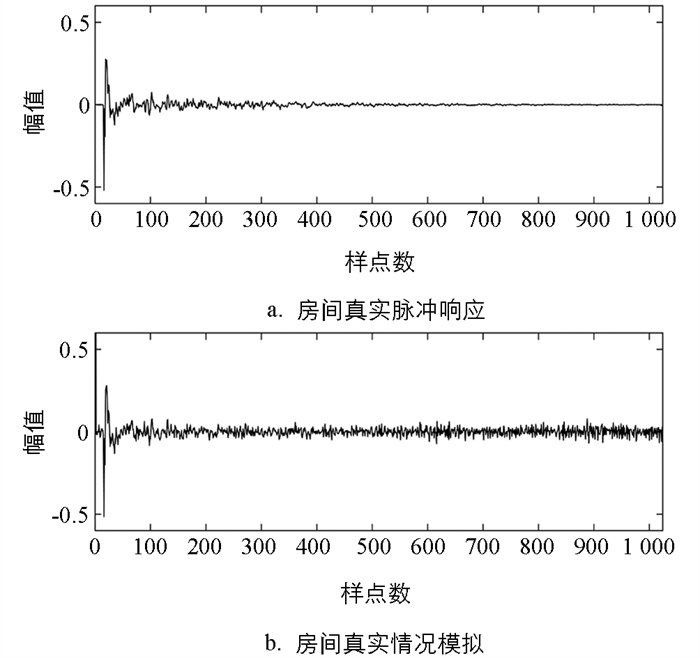
图 8是回声消除系统脉冲响应，图 8a是截取了1 024阶的房间真实脉冲响应，图 8b则是改进算法R-BS-NLMS对房间模拟出的脉冲响应，阶长同样选择1 024. 通过图 8a和图 8b对比可以看出，R-BS-NLMS算法很好地模拟出了真实房间的脉冲响应，将估计出的脉冲响应与输入语音信号做卷积运算即可得到回声估计.

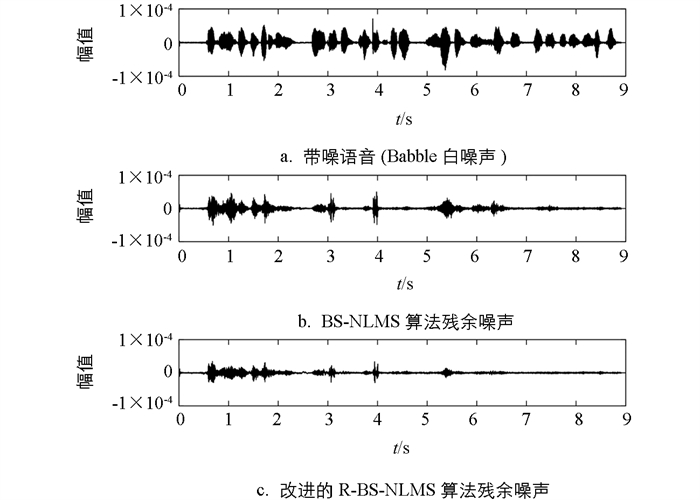
图 9给出了信号时域波形图，图 9a是加入Babble噪声后的带噪语音时域波形图. 图 9b和图 9c分别是BS-NLMS算法和R-BS-NLMS算法对带噪语音处理后的残余噪声，两种算法的步长参数均设置为0.1，由图 9b和图 9c信号幅度值对比可知，图 9c中改进的R-BS-NLMS算法残余噪声比图 9b中BS-NLMS算法残余噪声小，在幅值较大区域更为明显，收敛速度也略快. 在听感方面，利用audition软件将语音放大后播出，两种算法的回声抑制效果都很明显，特别是在与图 9a带噪语音对比时，能明显听出回声被抑制. 两种算法在工程中实践性都很好.

本文针对智能语音终端设备在复杂声学环境中由于回声抑制不佳而影响用户听觉体验的问题，提出了基于最小均方误差准则的R-BS-NLMS算法. 该算法使滤波器抽头权重的增加量在误差较大时趋近于零矢量，因而在环境冲激噪声下不会影响稳态误差情况，算法具有一定鲁棒性. 除此之外，还在参数分析部分推导出了均值收敛过程中步长参数的上下界. 仿真实验结果证明，本文提出的改进算法R-BS-NLMS相较于BS-NLMS算法降低了声学环境中冲激噪声的影响，且回声抑制效果明显. 由于自然界中广泛存在各种回声，本文的回声消除算法设计思路也会被应用于更加广泛的领域. 本文算法虽然在一定程度上改善了算法性能，但是计算复杂度仍然较高，不便于实际应用中操作. 因此，如何有效地降低算法复杂度将会是下一步研究的重点. 针对这种情况，部分更新方案、高阶统计量和仿射投影等将成为解决问题的重要手段，并广泛应用于如稀疏信道估计、水下噪声消除等领域.