-
目前LLE(局部线性嵌入)算法[1-2]广泛地应用于图像分类与目标识别问题中[3],但经典的LLE算法难以学习多个流形[4-8].本文在文献[9]的LLE算法的基础上,设计了基于LLE的多流形学习方法,通过局部非线性、多流形的方法学习并保留数据集的类结构.假设一个向量数据集为x1,x2,…,xN,ε是一个正实数,k是一个正整数,N(xi)表示xi的近邻点,包含了与xi距离最近的k个向量,即:对于每个xj∈N(xi),其欧式距离‖ xi- xj‖小于ε,将数据样本xi线性地表示为N(xi)中的近邻点.通过最小化(1)式计算权重值{wij}xj∈N(xi):
约束条件为∑xj∈N(xi)wij=1,wij>0;如果xj
$\notin $ N(xi),则wij=0.可将(1)式转换为:ε2=[xi-$\sum\limits_{j = 1}^k {} $ wij xj]2=[$\sum\limits_{j = 1}^k {} $ wij(xi-xj)]2=$\sum\limits_{jk} {} $ wijwik Gjk,式中Gjk=(xi- xj)T(xi-xk)是局部Gram矩阵,其中xj,xk∈N(xi).使用拉格朗日乘法计算重构权重${w_{ij}} = \frac{{\sum\nolimits_k {\mathit{\boldsymbol{G}}_{jk}^{-1}} }}{{\sum\nolimits_{lm} {\mathit{\boldsymbol{G}}_{lm}^{-1}} }}$ ,使用重构权重搜索d维的向量y1,y2,…,yn∈$\mathbb{R}$ d,这些向量定义了$\mathbb{R}$ d中原数据集的d维嵌入,其中d < D,通过最小化(2)式可获得d维的向量.其中
将(2)式改写为以下的矩阵形式:
式中:W是n×n的权重矩阵,mN×N=(I- Wn×n)T(I - Wn×n),Yi均正交.使用拉格朗日乘法计算最优解:
用(4)式对Yk(k=1,2,…,d)求导,YkTm-λkYkT=0则说明了mYk=λkYk,{λk}为m的特征值,{Yk}则是对应的特征向量.通过搜索m底部的特征向量可将E2(Y)最小化. Y0T的一个特征值为λ0=0,所以应当获得m底部的d+1个特征值及其特征向量,然后忽略Y0.
全文HTML
-
流形空间与欧式空间的拓扑相似.
定义1 流形M是一个度量空间,M具有以下的性质:如果x∈M,则存在一些x的近邻点U与整数n≥0,使得U与
$\mathbb{R}$ n同胚.假设ε>0是一个正实数,将流形中点x的近邻点定义为与x距离小于ε的点集合Nε(x)={ y ∈M:d(x,y) < ε},将流形M中每个点x表示为一个特征向量(a1,…,an)∈$\mathbb{R}$ n,其中xi∈x均为实数,将特征向量之间的距离d(x,y)定义为马氏距离:d(x,y)=$\sum\limits_{i = 1}^n {} $ | xi- yi|. -
首先考虑单类的分类问题:使用LLE算法对X进行处理,首先定义点xi∈X的k-近邻点,假设Nε(x)c表示近邻Nε(x)的各个元素.
定义2(k-近邻点) 假设ε>0,Nε,k(x)表示点x∈X的k-近邻点,定义为Nε,k(x)
$ \subset $ Nε(x),$\forall $ xi∈Nε,k(x),且$\forall $ xj∈Nε,k(x)c∩Nε(x),d(x,xi) < d(x,xj).以下证明数据集中如果任意两点xi与xj包含相同的特征向量,则xi与xj具有相同的k-近邻点.命题1 假设xi与xj均为
$\mathbb{R}$ D中的特征向量,如果xi= xj,则Nε,k(xi)∩Nε,k(xj)≠Ø.证 对于xi,xj∈
$\mathbb{R}$ n,如果xi= xj,则Nε(xi)=Nε(xj).根据定义2可得Nε,k(xi)$\subset $ Nε(xj),Nε,k(xj)$\subset $ Nε(xj),因此Nε,k(xi)∩Nε,k(xj)≠Ø. -
考虑多类的分类问题.为了简化分析,仅考虑两个类的分类问题,假设X是包含N+P个特征向量的数据集,F表示高维空间的数据点,假设前N个点属于类1,后P个点属于类2,假设c∈{1,2},L∈{N,P},X中每个特征向量xic的维度为D,xid=(xi,1c,xi,2c,…,xi,Lc)T,1≤i≤D.
传统的LLE算法无法同时学习多个流形,因为LLE算法中决定给定点的近邻点的过程忽略了类标签.由命题1知两个类的任意两点含有相同的特征向量,这两点则具有相同的近邻点,在流形学习中现有的算法无法保留流形的结构.
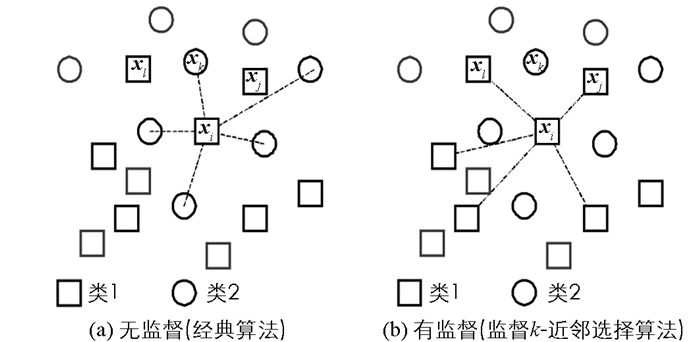
针对上述问题,为传统的LLE算法设计了一个近邻点选择机制,本方法在选择点xi近邻点的过程中考虑其类标签,将本方法称为监督k-近邻选择. 图 2所示,在寻找类1中点xi的k-近邻点过程中,经典方法也会考虑类2的点,因此,不属于类1的xk为xi的近邻点,而类1的xj与xl则不会变为xi的近邻点;本文方法中xk不是xi的近邻点,而xj与xl变为其近邻点,所以获得一个成功的流形重构过程.
定义3(监督k-近邻点) 假设C是X的一个数据类,如果点xi∈C
$\subset $ X的监督k-近邻点是Nε,k(xi),则xj∈C.定义4(等距算子[11]) 假设X,Y是线性的度量空间,x,y ∈X,如果X到Y的映射f满足条件:d(f(x),f(y))=d(x,y),则f是一个等距算子,即等距算子是一个保留了距离的映射.
选择监督k-近邻点与每个类中数据的等距算子,然后根据引理1可获得它们对应的流形.
引理1 假设X,Y是线性的度量空间x,y ∈X,一个等距算子f:X
$\xrightarrow{{}}$ Y将x的近邻映射到Y中f(x)的近邻.证 假设Nε(x)是点x ∈X的一个近邻点集合,假设等距算子将x映射到f(x),Nε(x)的每个点y满足d(x,y) < ε.根据定义4,因为d(f(x),f(y))=d(x,y),所以每个点y ∈Nε(x)
$\subset $ X映射至f(y)∈Nε(f(x))$\subset $ Y.引理2 假设X是线性的度量空间,C是X的一个数据类,对于任意点xi∈X,
1) 如果xi∈C
$\subset $ X,则Nε,k(xi)$\subset $ C;2) 如果xi∈C
$\subset $ X等距地映射至点yi∈M1,则Nε,k(yi)$\subset $ M1,其中M1是C中所有点获得的流形.证 根据引理1的定义,将Nε,k(xi)
$\subset $ X映射到Nε,k(yi)$\subset $ M,可得Nε,k(xi)$\subset $ C,因此Nε,k(yi)$\subset $ M1.根据引理1与2的结果可看出,通过流形内每个点的近邻点可重构其邻域,并保留流形的局部几何结构.下面通过本文的近邻选择方法对降维空间的流形结构进行比较.为了简便,本文规定如果至少有一个点xi1∈C1与点xj2∈C2使得xi1= xj2,则表示为C1δC2.
引理3 假设xi1与xj1是有限维线性空间X的任意两点,C1与C2是两个数据类,其中xi1∈C1
$ \subset $ X,xj2∈C2$ \subset $ X,如果xi1=xj2,则Nε,k(xi1)δNε,k(xj2).证 如果xi1=xj2,则Nε,k(xi1)∩Nε,k(xj1)≠Ø,因此Nε,k(xi1)δNε,k(xj2).
理论2 假设C1,C2
$\subset $ X,即X=C1∪C2,假设M1与M2分别是C1,C2获得的流形,如果C1接近C2,则M1接近M2.证 假设将xi1映射到点yi∈M1,xj2映射到点yj∈M2,则根据引理2可得Nε,k(yi)
$\subset $ M1与Nε,k(yj)$\subset $ M2,其中C1映射至M1,C2映射至M2.根据引理3可得Nε,k(xi1)δNε,k(xj2),根据引理2可将Nε,k(xi1)映射至Nε,k(yi),将Nε,k(xj2)映射至Nε,k(yi),所以Nε,k(yi)δNε,k(yj)$\Rightarrow $ M1δM2.在分类与模式识别过程中度量流形空间的距离具有重要意义.首先,考虑点到流形的距离,该距离对于流形空间中未知数据样本的分类极为重要.
定义5(点到流形的距离(PMD)) 假设x是有限维向量空间V中的一个点,M是一个流形,点x到流形M的距离d(x,M)定义为d(x,M)=
$\mathop {{\rm{min}}}\limits_{{S_i} \in M} $ d(x,Si)=$\mathop {{\rm{min}}}\limits_{{S_i} \in M} \mathop {{\rm{min}}}\limits_{y \in {S_i}} $ ‖x-y‖,式中Si是M的局部线性空间,因此M={Si:i=1,2,…,m},‖·‖是欧氏距离.在多流形空间中度量两个流形的距离也十分重要,因为本算法关注于保留每个流形的几何结构,通过测量多流形空间中两个流形的距离可比较降维空间中的流形距离,定义6定义了流形-流形距离.
定义6(流形-流形距离) 假设M1与M2是两个流形,则流形-流形有向距离定义为:
式中:TM1与TM2分别为M1与M2的长度,M1(i)是流形M1的第i个点.因为d(M1,M2)是有向距离,M1与M2的无向距离计算公式为:
-
本文基于LLE的多流形学习算法主要步骤如算法1所示.
-
假设一个D维数据集,大小为n,将C个数据类降维到d维空间,近邻数量设为k.文献[12]分析了传统LLE算法的计算复杂度,下文分析了本算法的计算复杂度.
本算法包含3个步骤:
步骤1每次k-近邻搜索的平均计算成本为O(Dlog(k)nlog(n)),因为本算法对各类独立地进行k-近邻搜索,所以平均成本为O(
$\sum\nolimits_i^C {} $ Dlog(ki)nilog(ni)),本算法在高维空间的改进明显地降低了近邻搜索的计算复杂度.步骤2中权重矩阵的构建成本为O(
$\sum\nolimits_i^C {} $ Dniki3),而传统LLE的成本为O(Dnk3).步骤3包含了两个子步骤:特征值分解的成本为O(dn2);最小化流形-流形距离的计算成本为O(
$\sum\nolimits_{i < J}^C {} $ dninj).步骤3是一个迭代过程,结束条件为最小化流形-流形距离达到预定的阈值,假设算法的迭代次数为m,则步骤3的计算复杂度为O(m(dn2+$\sum\nolimits_{i < J}^C {} $ dninj)).综上所述,本算法的总计算复杂度为:
2.1. 单类的单流形模型
2.2. 多类的多流形模型
2.3. 基于LLE的多流形算法
2.4. 计算复杂度分析
-
每个流形学习算法对训练数据进行流形学习,在流形空间建立测试数据样本之后,在低维流形空间使用k-近邻分类方法对样本进行分类处理,本算法的低维流形嵌入包含了多个流形.使用点-流形的距离(定义5)选择与给定的测试样本(xts)距离最近的流形,定义为:
假设d(dts,Mq)=minMi∈Md(xts,Mi),其中M=[M1,M2,…,Mq,…,MN]是流形空间,Mq是与类Cq对应的流形. Class(xts)=
$\left\{ {\begin{array}{*{20}{l}} {{C_q}}&{\rm{如果}}d\left( {{\mathit{\boldsymbol{x}}_{ts}},{M_q}} \right){\rm{ < }}{\varepsilon _{pmd}}\\ {{\rm{未决定}}}&{{\rm{其他情况}}} \end{array}} \right.$ -
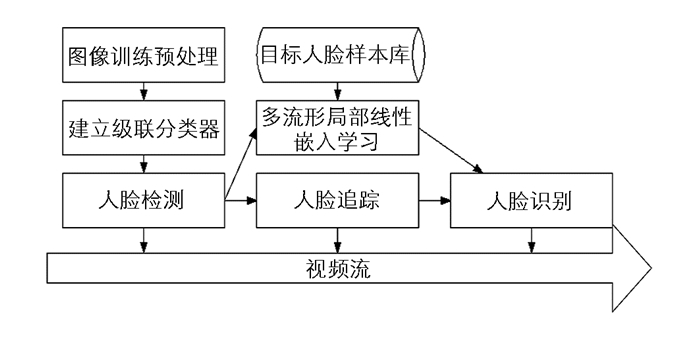
为了测试多流形算法对人脸识别与追踪的性能,选择两个公开的大规模视频数据集:YouTube Celebrities(YTC)[13]与COX[14],YTC广泛应用于视频人脸数据集的检测与追踪应用中,YTC共有47个主题、1 910个视频剪辑,其中大多数剪辑经过了高度的压缩且含有噪声,视频质量较低;COX则是一个大规模数据集,包含了1 000个主题,每个主题包含3个视频(不同摄像头拍摄),每个视频中大约有25~175个低分辨率的视频帧. 图 3,4所示分别是YTC与COX数据集的部分样本.
首先对COX数据集的所有人脸基于人脸边界框进行正则化处理,获得大小接近的人脸,采用文献[15]的方法对YTC数据集进行预处理:YTC的人脸缩放为20×20大小,COX的人脸缩放为32×40大小,对两个数据集进行直方图均衡化处理来消除光照效应.使用文献[15]的实验方案构建十折交叉检验,即随机选择10个训练集/测试集,YTC数据集的每折随机选择3个图像集作为训练集,6个作为测试集;COX数据集的每个主题有3个视频,从3个视频测试集(每个人)中选择一个视频作为训练集,剩下的两个视频作为测试集,因此,共需建立6个测试分组.
-
将本文多流形监督学习算法与无监督学习算法(MaxMD[16],CDL[17])、监督学习算法(SGM[19],GMM[20])进行比较,全面评估本算法的检测性能. 表 1所示是视频识别算法对YTC数据集与COX数据集的实验结果,全部结果均为十折交叉检验的平均识别率.从结果可看出,本算法对大规模视频数据集YTC与COX的检测结果均具有明显的优势,原因在于本算法通过多流形的学习策略有效地降低了问题的维度,提高了目标识别的准确率,此外,将流形空间中流形之间的距离作为一个度量指标,搜索数据的最优低维嵌入,最优的低维嵌入可提高分类准确率.
表 2所示是几种目标检测算法的计算时间统计,可看出本算法的训练时间较低,测试时间也较低,具有较好的实时性.
3.1. 本文流形学习算法的分类策略
3.2. 视频人脸的检测与识别实验
3.3. 实验结果与分析
-
经典的LLE算法难以学习多个流形,本文设计了基于LLE的多流形学习方法,通过局部非线性、多流形的方法学习并保留数据集的类结构.本算法设计了监督的近邻选择策略,将流形空间中流形之间的距离作为一个度量指标,搜索数据的最优低维嵌入提高分类准确率.通过寻找多流形空间中与同一数据样本距离最近的流形对已知数据进行分类,有效地保留了每个流形的结构并保持流形之间分离性.



 下载:
下载: