-
在遥感观测过程中,获取的全色图像具有较好的清晰度并且包含了较多的空间细节信息,但其光谱特性不是很理想.而获取的多光谱图像与之相反,具有较好的光谱特性,但其空间分辨率较差[1-2].为了获取包含较好空间分辨率以及光谱特性的遥感图像,需要将全色图像与多光谱图像进行融合.
近年来,遥感图像的融合已成为越来越热门的研究课题,国内外较多专家学者为获取较好的遥感图像融合效果,对遥感图像的融合方法进行了深入的研究.如Zhang等人[3]利用PCA变换来获取多光谱图像高频子带的字典,接着通过对获取的字典以及各个系数的计算完成遥感图像融合. Wu等人[4]通过PCA变换提取多光谱图像的第一主成分,接着通过Curvelet变换对图像进行尺度分解,进而完成遥感图像融合.以上方法都能够实现遥感图像的融合,但由于PCA变换存在光谱退化的问题,使得融合后的遥感图像存在光谱失真的不足.对此,Luo等人[5]通过平移不变Shearlet对图像进行尺度分解后,接着通过区域相似度融合策略完成高频图像的融合;该区域相似度融合策略利用比值法选择全色图像或多光谱图像中的其中一个高频子带作为高频融合系数,忽略了另一高频系数所包含的信息,易导致融合图像出现模糊现象.古丽米热等人[6]利用二进小波变换对图像进行分解,制定了高低频融合策略完成遥感图像的融合.基于小波变换的遥感图像融合方法能够对遥感图像进行精细分解,克服光谱退化,实现遥感图像融合.但是小波变换方法分解的图像具有各项同性特征,不能较好地表述图像边缘等信息,使得融合图像效果不佳.
为了使融合后的图像具有较好的光谱特性并且包含更多细节信息,本文提出了一种基于非下采样Contourlet变换耦合锐度制约模型的遥感图像融合算法.首先引入IHS变换提取多光谱图像的I分量,通过非下采样Contourlet变换对I分量与全色图像进行尺度分解,从而获取各自对应的高、低频子带;然后利用像素点邻域的像素值之差构造锐度制约模型,完成低频子带的融合,用以克服低频子带中灰度畸变造成的锐度值误判,避免融合图像中块效应等不良现象的出现;接着通过全色图像与I分量的高频子带特征构造高频子带融合模型,用以完成高频子带的融合,并通过非下采样Contourlet逆变换与IHS逆变换获取融合遥感图像.最后,测试所提算法的融合质量.
全文HTML
-
IHS变换通过I(亮度)、H(色调)、S(饱和度)3个分量来对人类视觉系统中的颜色特征进行描述.与常见的RGB颜色模型相比,IHS变换中亮度、色调、饱和度3个分量之间通道的相关性更小,能够更精确地描述图像的颜色特征. IHS变换中I分量能够对图像的亮度进行较好的描述.全色图像与多光谱图像融合过程中,先把多光谱图像从RGB空间变换到IHS空间.接着将全色图像进行灰度拉伸,使得其对应的灰度均值与方差,同IHS空间的I分量一致.将拉伸后的全色图像视为新的I分量,通过IHS逆变换,便可将多光谱图像的光谱信息与全色图像的空间信息进行融合.首先,将图像的RGB空间转换到IHS空间[7-8]:
式中,v1与v2为中间变量.
-
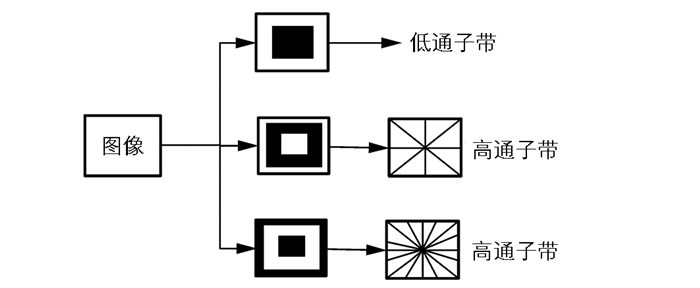
通过IHS变换获取多光谱图像中的I分量后,对其与全色图像进行多尺度分解,以获取图像的低频子带与高频子带.小波变换是一种常用的尺度分解方法,其具有良好的时频局部化特性以及多尺度性,能够对图像进行无冗余分解.但由于小波变换受到分解方向的限制,使得融合图像出现模糊效应[9-10].而Contourlet变换在继承了小波变换优点的基础上,克服了小波变换受方向限制的缺点,其具有良好的各向异性以及非线性逼近特性.但Contourlet变换不具备平移不变性,使得融合后图像存在一定的振铃效应[11-12].对此,A.L.Cunha等人提出了非下采样Contourlet变换,它通过非下采样的塔式分解(NSP)以及非下采样的方向滤波器(NSDFB)对图像进行分解.非下采样Contourlet变换继承了Contourlet变换的多尺度以及多方向特点,同时还具有平移不变性,使得分解图像能够包含更多的细节信息,提高融合图像的质量.对此,本文将采用非下采样Contourlet变换对全色图像以及多光谱图像的I分量进行多尺度分解.
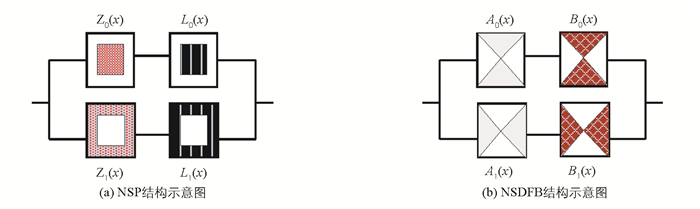
非下采样Contourlet变换过程如图 2所示,其借助NSP与NSDFB将多尺度与多方向的分解分开独立进行[13-14].其中NSP负责将图像进行多尺度分解以获取多尺度的子带系数,NSDFB负责将多尺度子带系数进行多方向分解,以获取多尺度、多方向的子带系数. NSP与NSDFB的结构示意图如图 3所示. w级NSP分解的滤波器可表述为
其中,Z0与Z1表示图 3中的NSP滤波器组,Π表示求乘积运算.
w级NSDFB分解后所得的低频子带数量为1个,高频子带数量为
$\sum\nolimits_{r = 1}^\mathit{w} {{2^{{w_r}}}} $ 个.在非下采样Contourlet变换过程中所获得的子带系数都具有与源图像相同的尺寸,以便于融合过程中寻找对应的子带系数.以图 1(b)为对象,对其进行2级非下采样Contourlet变换,结果如图 4所示.
1.1. IHS变换
1.2. 非下采样Contourlet变换
-
本文所提的基于非下采样Contourlet变换与锐度制约模型的遥感图像融合算法过程见图 5.其详细的过程如下:
1) 对多光谱图像进行IHS变换,提取多光谱图像的I分量.
2) 通过非下采样Contourlet变换,对多光谱图像的I分量以及全色图像进行多尺度精细分解.使得获取的低频子带与高频子带能够保留更多源图像的细节信息,有效提高融合图像的质量.
3) 获取图像的子带系数后,将对图像的子带系数进行融合.图像的清晰度与图像中灰度的变化有着密切的关系,灰度变化越为剧烈时,图像的锐度值越大,图像越清晰,反之图像越模糊.本文将通过低频子带中像素点邻域的像素值之差构造锐度制约模型,用以完成低频子带的融合,使图像具有更高的清晰度.
四邻域Laplace算子具有良好的灵敏性,能够较好地对图像锐度进行表述[15-16].由此本文首先通过低频子带系数中任意像素点p的四邻域像素值构造Laplace算子.
令如图 4所示图像中任一像素点p以及其四邻域点p1,p2,p3,p4的像素值分别为p(x,y),p(x+1,y),p(x-1,y),p(x,y+1),p(x,y-1),则构造的Laplace算子▽2p(x,y)为
其中,
$\frac{{{\partial ^2}p\left({x, y} \right)}}{{\partial {x^2}}}$ 与$\frac{{{\partial ^2}\left({x, y} \right)}}{{\partial {y^2}}}$ 的表述如下:其中,
$\partial $ 是求导运算;▽2为Laplace算子.通过▽2p(x,y)构造式(9)所示的锐度度量模型,用以对图像中像素点p的锐度进行度量:
其中,Rp(x,y)代表对像素点p(x,y)的锐度度量结果.
为了避免由于像素点灰度畸变引起的误判,可通过式(9)构造区域锐度度量模型Q:
其中,n与m表示以p点为中心所构成邻域的行、列尺寸.
令da与db分别为不同图像的低频子带系数,通过式(10)构造锐度制约模型,用以求取低频子带的融合系数Rd,
式中,Qpa(x,y)与Qpb(x,y)分别表示不同图像某像素点处的区域锐度值;k为均衡因子,
完成低频子带系数的融合后,将对高频子带系数进行融合.高频子带包含了图像中较多的细节信息,为了在多保留光谱信息的基础上,对全色图像的空间信息进行保留[17-18].在此以多光谱图像中I分量的高频子带特征为基础,结合全色图像的高频子带特征构造高频子带融合模型,用以完成高频子带的融合.
令TI为多光谱图像中I分量的高频子带系数,TP为全色图像的高频子带系数,TI与TP的共有特征用A表示,则
TP的独立特征B表述为:
通过独立特征B与TI构造的高频子带融合模型F为
其中,D(x)表示求取以x为中心的邻域中系数的标准差.
完成子带系数的融合后,可通过非下采样Contourlet逆变换获取新的亮度分量I′.再将I′与H,S分量进行IHS逆变换,以获取融合后的遥感图像.
-
在Intel core双核CPU、4GB内存的计算机上以VC6.0软件作为仿真环境进行实验.同时,为了突出所提技术的优势,选取文献[9]及文献[12]方法作为对照组.
不同方法融合的遥感图像分别如图 6和图 7所示.其中图 6为不同方法对IKONOS卫星拍摄某山地的全色图像(见图 6(a))与多光谱图像(见图 6(b))的融合效果,图 6(a)与图 6(b)的大小为512×512像素. 图 7为不同方法对SOPT5卫星拍摄地区的全色图像(见图 7(a))与多光谱图像(见图 7(b))的融合效果,图 7(a)与图 7(b)的大小也为512×512像素.
通过图 6(c)可见,通过文献[9]方法融合的图像亮度偏亮,而且河道边缘存在伪吉布斯效应,较模糊.通过图 6(d)可见,通过文献[12]方法融合的图像中存在光谱失真现象,使得河道中水的颜色偏蓝,部分草地的颜色变成了白色,而且河道边缘存在一定的模糊效应.通过图 6(e)可见,本文方法融合的图像光谱特性较为正常,而且河道边缘等细节都较为清晰,仅部分草地的颜色偏白.通过图 7可见,文献[9]方法融合的图像(见图 7(c))存在较为严重的光谱失真现象,绿色树木的颜色较浅,而且屋顶轮廓模糊不清.文献[12]方法融合的图像(见图 7(d))中存在一定的振铃效应,使得建筑物与建筑物之间的间隔变窄,而且树木附近的土地由于光谱失真变成了绿色.本文方法融合的图像(见图 7(e))建筑物之间的间隔正常,而且树木的颜色也较为正常,仅部分树木附近小块土地的颜色偏绿.由此可见,本文方法融合的图像具有较好的光谱特性以及较好的清晰度.因为本文采用IHS变换对多光谱图像进行分解,并通过IHS逆变换完成图像的融合,使得多光谱图像的光谱信息与全色图像的空间信息能够有效地进行融合.另外,本文还通过低频子带中像素点邻域的像素值之差构造锐度制约模型,从图像的区域锐度特征出发,用以对低频子带进行融合,保证了融合图像的锐度特征,从而使得融合图像具有较好的光谱特性以及较好的清晰度.
峰值信噪比(Peak Signal Noise Rate,PSNR)能够较好地反应出图像中所包含的细节成分,其值越高表示图像中所包含的细节信息越多,图像就越清晰.光谱角(Spectal Angle Mapper, SAM)能够对图像中光谱信息的失真度以及完整度进行度量,其值越大表示图像中光谱信息失真度越大,完整度越差[19-20].为此,将QuickBird卫星拍摄的15组多光谱图像以及全色图像作为测试对象[21-22],利用不同方法对测试图像进行融合,并对融合图像的PSNR以及SAM值进行测试.
不同方法融合图像对应的PSNR以及SAM值分别如图 8以及图 9所示.从图 8可见,本文方法融合图像的PSNR值始终为最大.从图 9可见,本文方法融合图像的SAM值始终为最小,说明本文方法融合的图像具有较好的光谱特性以及包含了较多源图像的细节信息.因为本文采用了具有多尺度、多方向以及平移不变性的非下采样Contourlet对图像分解来获取高、低频子带,使得分解图像能够包含更多的细节信息,从而提高了融合图像的质量.同时本文还通过多光谱图像中I分量的高频子带特征,与全色图像的高频子带特征构造了高频子带融合模型,用以完成高频子带的融合,较好地保留了多光谱图像的光谱特征以及全色图像的空间特征,进一步提高了融合图像的质量.文献[9]方法通过自适应显著模型对多光谱图像与全色图像进行显著性检测,接着通过双树复小波对图像进行分解,最后将显著性检测结果融入图像融合策略中完成图像融合.由于双树复小波对图像分解时,受到方向性的制约,使得分解图像中存在光谱失真以及模糊等现象,导致融合图像质量不佳.文献[12]方法通过Contourlet变换对图像进行分解,接着利用加权平均的方法融合低频子带,通过广义高斯参数估计的方法融合高频子带,进而完成图像融合.由于Contourlet不具备平移不变性,使得融合图像存在振铃效应.另外,加权平均的方法虽然较为简单,但该方法没有对各个图像的细节信息进行分析,而是直接加权平均,这样使得融合图像的光谱信息存在失真现象,从而降低融合图像的质量.
-
本文在非下采样Contourlet变换的基础上,利用图像的锐度值设计了一种基于非下采样Contourlet变换耦合锐度制约模型的遥感图像融合算法.文中首先通过IHS变换获取多光谱图像的I分量,利用非下采样Contourlet变换对I分量与全色图像进行多尺度分解,得到其对应的高频子带与低频子带,然后在低频子带中像素点邻域像素值之差的基础上,构造锐度度量模型和区域锐度度量模型,完成低频子带的融合.接着考虑融合图像包含源图像更多的细节信息,利用I分量以及全色图像的高频特征构造了高频子带融合模型,用以完成高频子带的融合.最后将融合后的高、低频子带进行非下采样Contourlet逆变换获取新的I分量I′;再将I′与H,S分量进行IHS逆变换,完成遥感图像融合.实验结果表明,本文所提方法融合的图像中包含了更多的细节信息,同时也具有较好的光谱特性.




 下载:
下载: