根据量子力学内重要的“不确定性原理”^[7]可知, 无法找到满足窗口面积不大于以Gaussian^[8]为窗函数时对应的面积数值的理想窗函数.理想的做法使是用Gabor函数进行处理, 该函数是由Gaussian与合适的调制函数组合形成的, 能够满足频域与空域的相关要求.

用于边缘检测的线性Gabor滤波器, 其方向和频率均和人类的视觉系统极为相似.其中二维的Gabor滤波器是一个正弦平面波与高斯核函数的乘积, 学者Daugman曾经给出的定义形式为:

其中: ω₀表示复正弦函数的频率; σ_x与σ_y表示高斯包络在X与Y轴向的标准差数值.

因为(1)式的虚部用于提取目标特征更具有优势, 需求解(1)式Gabor函数的虚部:

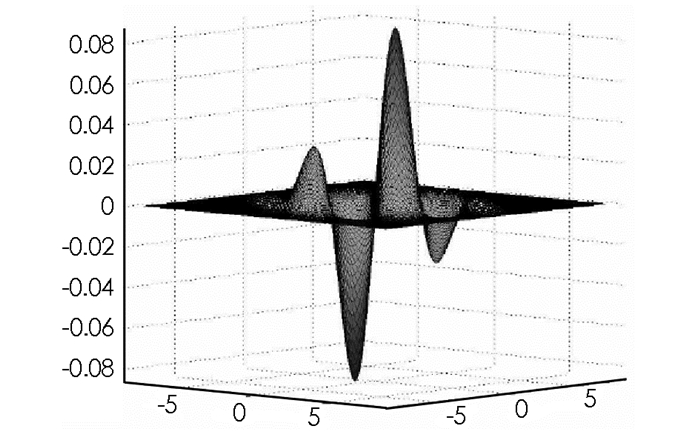
如果取σ_x=σ_y=2, ω₀=1, x₀=y₀=0对应奇函数的仿真效果见图 1.

由于Gabor滤波器需在对应小波族的前提下实施离散化操作, 所以, 需要在〈Ψ, Ψ〉=1条件下进行归一化处理, 并假设σ_x=σ_y, $ \sigma = \frac{k}{{{\omega _0}}}$可得:

式中θ为滤波器的旋转角度.根据文献[9]k的值为:

式中Ω为阶跃带宽.

根据(3)式可知, Gabor函数可以看作Gaussian函数经复正弦函数处理后得到的, 其中θ和ω₀值可以构成Gabor滤波器组. θ和ω₀的定义如下:

式中:n为所采用的滤波器所包含的角度的总和, θ_k为第k个角度; m为滤波器包含的频率的个数; ω_k为第k个频率.在实验中, 我们设定的参数如下:Ω=1; $\theta = 0, \frac{\pi }{5}, \frac{{2\pi }}{5}, \frac{{3\pi }}{5}, \frac{{4\pi }}{5};{\omega _0} = 1, \sqrt 2 , \frac{{\sqrt 2 }}{2}, \frac{1}{2} $.该小波滤波器组由5×4=20个滤波器组成.

由于Gabor滤波器具有位移不变性和旋转不变性的特点, 因此, 进行特征提取时, 不需要事先进行准确地定位操作, 同时对目标移动现象很迟钝^[10-11].

特征提取时, 首先将64×64的场景256灰度图像I (x, y)同小波滤波器进行卷积:

(7) 式中卷积的具体计算采用FFT算法:

式中i和j代表不同的角度和频率.每一幅64×64的场景灰度图像I(x, y)经(8)式变换后得到20幅Q_{i, j}(x, y).卷积操作产生大量的Gabor小波特征(64×64×20), 其特征数目远远多于原始图像个数.由于Gabor函数本身的非正交性, 决定了图像经过Gabor小波滤波器得到的Gabor域响应值包含了大量的冗余信息, 而这些冗余信息对于图像的特征表达没有太大的意义, 因此需要在响应值里找到最能表达图像特征的特征点.

为了增强系统的鲁棒性, 采用主元分析法(PCA)对图像特征进行降维.它的重要特性就是在均方误差最小的意义下用低维子空间来表示高维原始数据.

将20幅滤波后图像Q_{i, j}(x, y)分别按行展开, 组成20个4096维的列向量X_i, 并中心化:

式中K为Q_{i, j}(x, y)的数量.由X_i^*生成扩展矩阵M:

其中M是一个4096×4096正定实对称矩阵.求出其特征值λ_i和相应的特征向量V_i.

与较大特征值相对照的向量能够描述目标的整体轮廓, 与较小特征值相对照的向量对于目标微观成分的表达比较清楚.按照大小顺序, 把前P个特征向量提取出来当成对应子空间的基.确定P的大小时, 应该依据经验事先选定阈值T的大小:

式中N是X_i的维数.在本文取T=90, 这样可以尽可能保全图像数据, 使实验结果相对准确.

SVM主要用于解决小样本、非线性以及高维识别等分类问题^[12].本文将SVM理论引入到机器人目标搜寻的技术上面, 仅仅对少数的设定目标特征进行识别.

训练样本有限情况下的机器学习规律统计学习理论是按照变换原则把输入数据映射进高维特征区域内, 接着在该区域内构建最优分类面.因为该操作的难度较大, 而使用支持向量机的理论能够免除高维空间所涉及的运算工作, 仅在训练样本范围内实施内积计算, 需要进行的运算要依据预定的核函数来完成.目前还没有好的方法来解决核函数的选取问题, 比较成熟的核函数及其参数的选择都是根据经验来选取.本文采用径向基核函数, 表示如下:

此时只需保证Mercer条件成立, 区域内积即可进行相关变换操作, 避免复杂计算.此时, 最优分类函数变为:

式中: n为样本数; α_i^*为Lagange系数; b_i^*为分类器阈值.在样本数据中, 非支持向量对应的α_i^*均为0, 因此(13)式的求和实际上只对支持向量进行.

考虑到机器人在线运行实时性的要求, SVM分类器采用“一对多”策略.设经训练后每个分类器的分类函数为f_j(xX), j=1, 2, …, n对于任意待分类场景的特征矢量xX, 存在k∈{1, 2, …, n}, 使得:

则判定该目标属于第k类.

实验在自行研制的CY-1型全自主移动机器人上进行, 如图 2所示.机器人CPU为P4 3.0 GHz, 内存512 MB, 编程环境为VC++6.0, 视频采集图像每帧分辨率截取为64×64, 灰度级为256.

利用CY-1型移动机器人上的CD摄像机摄取不同角度不同距离的3种目标物体(足球、工具箱、小机器人)组成图像数据库.数据库中包含了每个物体在0°-365°每隔5°不同方向和0.5 m, 1 m, 2 m不同距离(地面距离)拍摄的样本.样本总数共72×3×3=648个, 并将其分成训练样本和测试样本.每个物体取12×3=36个样本做训练样本, 共36×3=108幅图像.其余540幅图像作为测试样本.部分样本如图 3所示.

通过(8)式对每个训练和测试样本提取图像特征, 并经(11)式选取阈值使每幅图像的特征值从4 096个降为54个.将其输入到SVM训练器和分类器中, 使用(12)式作为核函数进行SVM训练和分类.测试结果如表 1所示.

由表 1可知, 3种不同的目标物体经训练和分类后, 识别率都超过了92%.由于测试样本与训练样本中目标物体的角度不同, 因此该算法具有一定的鲁棒性.

在室内地毯上, 随机放置工具箱、球、小机器人等物体, 移动机器人作旋转跟踪物体实验.移动机器人上CCD摄像机采集视频图像, 视频采集速度设置为10 fps.视频采集程序开发环境为VC++6.0, 图像处理程序基于VFW(Video for Windows)开发.在每帧视频图像上绑定一命名为cap_Video_Stream_Callback()的回调函数, 该回调函数捕获视频图像, 并调用相关的图像处理函数处理图像.为得到实验识别时间的准确数据, 在回调函数cap_Video_Stream_Callback()中以调试版本的形式调用多媒体定时函数time_Get_Time(void), 并利用该函数计算识别完成时所需的时间. time_Get_Time(void)函数返回值为系统开机时间, 其计时精度为1 ms, 满足实验要求.在下一帧图像到来前, 如果本帧图像识别尚未完成, 则自动忽略下一帧图像, 直至识别完成为止.当移动机器人能自动搜索上述几种物体, 并移动到物体跟前, 则测试成功.识别对象的平均时间见表 2.

由表 2可知, 虽然本文采用的方法识别率在93%左右, 但由于图像是连续的, 当某一帧识别出现错误时, 可以在下一帧得到弥补, 因此, 最终实验成功率为100%.从识别时间看, 变化较大, 但基本能保证8 fps的图像处理速度.

本文提出了一种用于移动机器人目标识别的基于灰度图像的目标识别方法.该方法通过Gabor滤波器和PCA方法提取图像特征, 并通过SVM对其进行分类, 实现了基于256灰度图像的目标识别.