-
图像修复技术成为了当下数字图像处理技术的研究热点之一.图像修复的本质是利用图像破损区域以外的已知信息对破损的局部信息进行有效重建,使得修复出来的图像能够近似原图像的整体视觉[1-3].近几年涌现了许多图像修复算法[4-7],但是这些算法大都忽略了图像块的显著边缘特性,使得修复图像出现模糊效应以及不连续效应等不良现象.
对此,本文提出了一种基于曲率约束因子耦合边缘加权法则的图像修复算法.将通过等照度线构造的曲率约束因子加入优先级的计算,构造了优先级度量函数,对待修复像素点的优先级进行度量,确定优先修补块.通过像素点之间的均值差构造了像素自相关模型,进而对样本块大小进行调节.利用样本块显著边缘构造的边缘加权模型,联合SSD模型建立了边缘加权法则,搜索最优匹配块完成图像修复.仿真实验表明,本文所提算法具有良好的鲁棒性能以及修复性能.
全文HTML
-
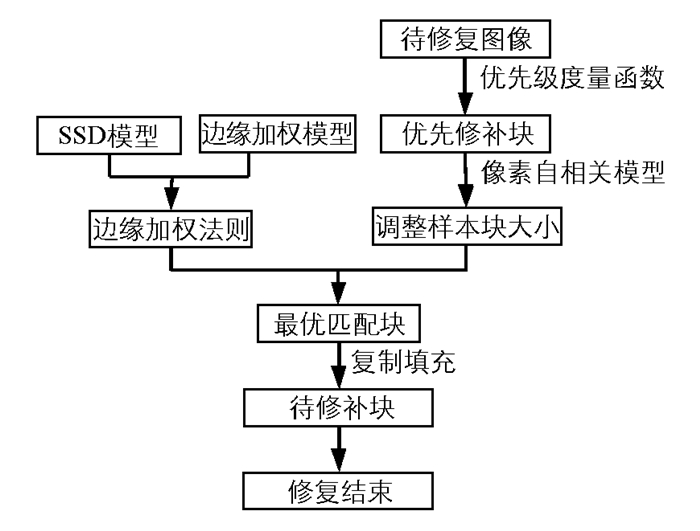
本文图像修复算法利用等照度线方向构造曲率约束因子对数据项进行改进,构造优先级度量函数从损坏区域中选取优先修补块,为图像修复的有序性提供了保障.通过像素点之间的均值差构造了像素自相关模型,调整了样本块的大小,提高了算法的修复质量以及修复效率.利用样本块显著边缘构造了边缘加权模型,并以边缘加权模型以及SSD模型为基础建立了边缘加权法则,实现了对最优匹配块的精确搜索.本文算法设计的流程图如图 1所示.
-
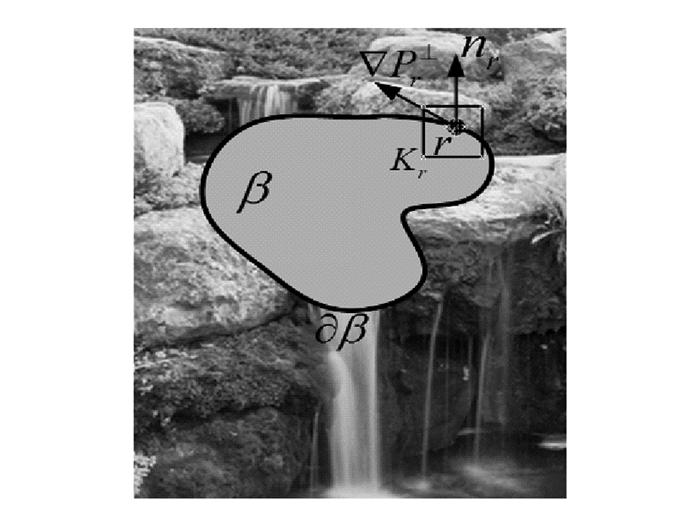
在如图 2所示的图像P中,θ表示待修复区域,β=P-θ表示源区域,源区域与待修复区域的相交处用∂β表示.令r为∂β上的一个待修复像素点,Kr为以r为中心的一个待修补块.则其优先修补块选择函数可表述为[8-9]:
其中C(r)和D(r)分别为置信度项以及数据项,C(r)和D(r)的表达式分别如(2)式和(3)式所示.
其中:|Kr|为待修补块Kr的面积,∇Pr⊥和nr分别为像素点r处的等照度线方向以及法线向量[10].
对于待修补块而言,其纹理连续性与等照度线的曲率有着一定的关联,等照度线的曲率越小,则表示待修补块对应的纹理连续性能越理想,该待修补块的优先级就越高[11-12].对此,本文通过等照度线方向构造了曲率约束因子:
将曲率约束因子带入(3)式对数据项进行改进:
其中δ和ε为调节因子.通过实验得出δ取值为2,ε取值为0.3.
将改进的数据项
$ \overline {D(r)} $ 带入(1)式,便构造出了本文的优先级度量函数:利用优先级度量函数对待修复区域中的所有待修复像素点的优先级进行度量,选取优先级最大值像素点对应的待修补块作为优先修补块.
-
利用固定大小的样本块进行图像修复,难以适应图像纹理结构的变化需求,导致修复图像容易出现不连续效应以及块效应等[13-14].对此,本文将利用像素点的均值之差构造像素自相关模型,对样本块的大小进行调整.
令图像的尺寸为M×M,w(x,y)为待修补块中一个已知像素点,选择与w(x,y)之间的距离为m的4个像素点w(x-m,y),w(x+m,y),w(x,y-m),w(x,y+m),通过求w(x,y)与这4个像素点的均值之差来得到像素差值Dw(x,y):
通过Dw(x,y)与其4个相邻像素差值的均值相乘,即可构造像素自相关模型,对样本块的大小进行调整.构造的像素自相关模型表述如下:
其中n表示待修补块中已知像素点的个数.
通过求取像素点对应的RZ值,通过下述调节模型,便可求出样本块的大小SZ:
其中TS为预设阀值.
-
当前较多图像修复算法往往只注重于对待修补块的整块修复,而忽略了待修补块的边缘特征,导致修复的图像中存在不连续效应以及振铃效应.为了克服这些不足,利用样本块显著边缘为约束,构造边缘加权模型.建立以边缘加权模型联合SSD模型为基础的边缘加权法则,对最优匹配块进行搜索,用于对待修补块进行修复.具体的边缘加权法则表述如下:
首先,建立边缘加权模型.令Kr为以像素点r为中心的一个确定尺寸的样本块,ri及r′i为Kr中任意两个像素点则构造的边缘加权模型如下:
其中Br表示Kr的显著边缘,可通过蚁群优化算法[15-16]进行检测. E(r,ri)定义如下
其中(x1,y1)与(x2,y2)分别为r与ri的坐标.
其次,引入SSD模型,
其中:Kz表示源区域中的匹配块;Rx,Gx,Bx表示像素点x对应的红色、绿色、蓝色分量[17-18].
最后,联合(11)式和(12)式形成最优匹配块搜索模型:
通过(13)式从源区域中选取最小P(Kr,Kz)值对应的匹配块Kz作为最优匹配块.
1.1. 选取优先修补块
1.2. 调整样本块大小
1.3. 搜索最优匹配块
-
本文实验将MATLAB 7.0软件作为仿真工具,在Intel酷睿I5 2.4 GHz双核处理器、500 GB硬盘、2 GB内存、Windows 7.0操作系统的计算机上进行仿真测试.实验采用对比方法,将文献[19]以及文献[20]中的图像修复算法作为对照组,以对本文算法的修复性能进行对比.
-
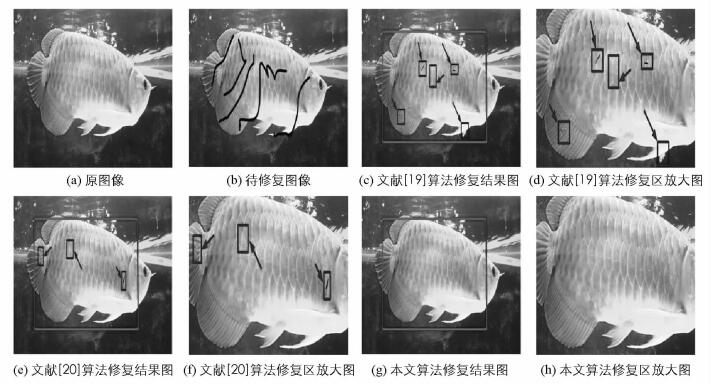
不同算法对灰度图像以及彩色图像的修复效果对比分析图分别如图 3和图 4所示.由图 3可知:文献[19]算法(图 3(c))存在残留效应以及块效应;文献[20]算法(图 3(d))存在模糊效应以及振铃效应;而本文算法修复结果图(图 3(e))不存在不良现象.由图 4可知3种算法都具有较好的修复效果,但是将不同算法的修复区放大对比可见:文献[19]算法(图 4(d))存在不连续效应以及修复残留;文献[20]算法(图 4(f))存在不连续效应以及模糊效应;本文算法(图 4(h))具有最好的修复效果,不存在这些不良效应.修复效果说明本文算法具有较理想的修复性能以及较好的鲁棒性能,能克服修复过程中产生的块效应以及不连续效应等不足.究其原因为本文利用等照度线方向构造了曲率约束因子,对数据项进行改进,构造了优先级度量函数,从损坏区域中选取了优先修补块,为图像修复的有序性提供了保障,提高了算法的修复质量.同时本文还利用样本块显著边缘为约束,构造边缘加权模型.建立以边缘加权模型联合SSD模型为基础的边缘加权法则,对最优匹配块进行搜索,有效对不连续效应等不良效应进行了抑制.
-
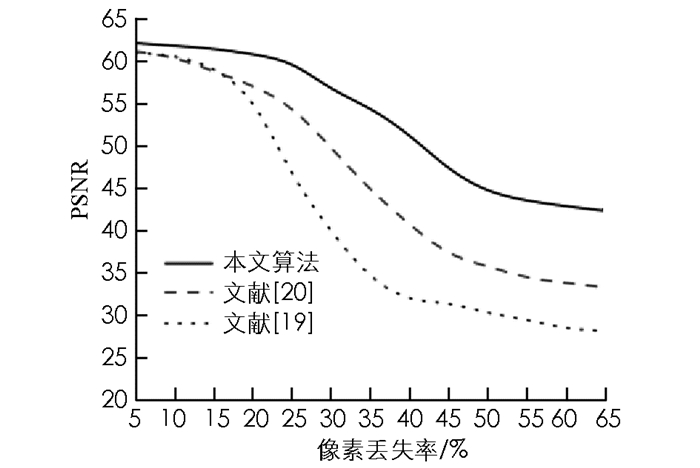
峰值信噪比对比图通过量化测试的方法对本文算法的修复性能进行测试.峰值信噪比(Peak Signal to Noise Ratio,PSNR)能够在一定程度上对修复后图像与原图像的近似度进行客观反映.对此,本文将修复后图像的峰值信噪比作为量化指标.测试过程中将图 4(a)作为测试目标,测试方法为对测试目标设置不同程度的像素丢失比例,通过不同算法对其进行修复,并求取修复后图像的峰值信噪比.
图 5为不同算法修复图像的峰值信噪比对比图.与图 5可知,本文算法修复的图像具有较高的峰值信噪比,和原图像的近似度最高.因为本文通过像素点之间的均值差构造了像素自相关模型,调整了样本块的大小,提高了算法的修复质量.同时本文还将样本块的边缘特性加入最优匹配块的搜索方法中,提高了最优匹配块的搜索精度以及正确度,使得算法的修复效果进一步得到了提升.
2.1. 不同算法修复效果对比分析
2.2. 不同算法量化测试对比分析
-
本文提出了一种基于曲率约束因子耦合边缘加权法则的图像修复算法.通过等照度线方向构造的曲率约束因子形成优先级度量函数,从待修复区域中选取优先修补块,使得算法能按照更为有效的修复次序进行修复.利用像素点之间的均值差构造了像素自相关模型,实现了样本块大小的调节功能,使得算法修复图像的质量以及算法的修复效率得以提高.以构造的边缘加权模型与SSD模型为基础,建立了边缘加权法则,准确选取最优匹配块,使得算法的修复质量以及算法的鲁棒性能进一步得到了提高.



 下载:
下载: