-
由于连铸生产过程复杂,生产环境比较恶劣,氧化铁皮和铸坯表面水膜等因素严重影响了传感器测温的准确性,因此连铸方坯表面测温一直是一个难点.许多研究者[1-4]采用基于凝固传热数学模型来计算铸坯表面温度,虽然能得到较为准确的结果,但是凝固传热数学模型的计算量很大,难以满足动态控制和优化的要求.
文献[5-7]采用Hopfield神经网络构造出能量函数,以最小化能量函数为目标来求解抛物型偏微分方程,开创了以神经网络求解偏微分方程的新方法.由于Hopfield是全反馈型的网络,其网络结构复杂并且网络要求权值矩阵是对称的才能保证动态神经网络的稳定性[8],因此Hopfield网络求解抛物型偏微分方程有着较大的局限性.文献[9]采用BP神经网络来预测连铸二冷区某一区段内的平均温度取得了较好的结果.文献[10-11]采用BP网络建立了连铸方坯温度预测模型,取得了较为准确的结果,但其采用的是前向网络难以反映温度动态变化过程.文献[12]中提出了一种GA-BP神经网络方法实现在板坯连铸模型断口预测,预测精度高于传统BP神经网络方法.
以上文献中是不同神经网络方法对模型板坯连铸模型的预测,虽然各自拥有不同的优势,但对于本文连铸方坯温度的预测需要动态预报,以上方法在这方面具有局限性.时滞BP神经网络可以反映动态过程的变化,因此可以用来描述温度场的动态变化.本文提出时滞BP神经网络方法来近似连铸二维传热模型,以当前时刻温度场、冷却水量和拉速作为神经网络的输入,输出为下一时刻温度场.该方法计算时间大大减少,实验结果表明该时滞BP神经网络模型能够较为准确地计算出铸坯表面温度,具有一定的应用价值.
全文HTML
-
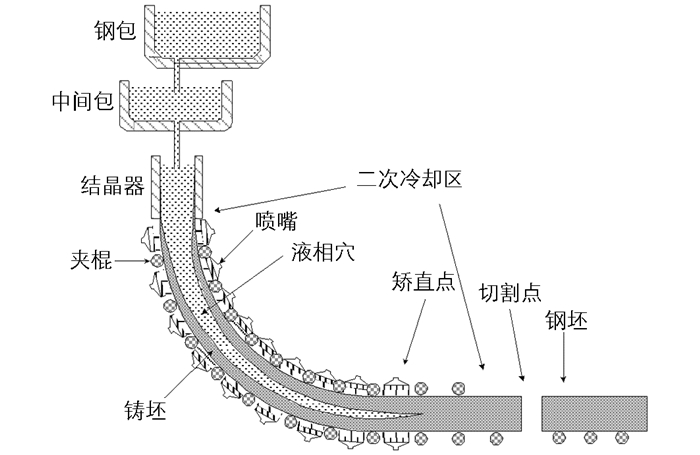
作为钢铁生产中一个重要的环节——连铸,其过程就是在冷却过后形成质量合格的钢坯.本文针对弧形连铸机建模,其结构见图 1.通过一冷区迅速降低铸坯表面温度,然后再经过二冷区高温钢水实现从液态到铸坯的过渡.
在弧形连铸机的建模过程中需要对实际情况做一些假设,才能用数学模型对连铸机进行建模,采用Fourier导热定律对弧形连铸机进行建模.
建模前需要对现实模型中的部分内容做忽略处理,下面1)-4)给出了需要忽略的内容.因为产生的影响较小,所以可以忽略,如3)中拉坯方向的热量仅为总热量的3%~6%:
1) 忽略因凝固、冷却造成的铸坯尺寸变化;
2) 忽略流场温度的影响;
3) 忽略拉坯方向的热量;
4) 比热容的计算采用等效比热法.
在3个忽略和1个等效的假设条件下,对连铸凝固传热二维模型建模,得到导热微分方程为
其中ρ表示钢密度,Ce表示比热,T和t分别表示二维温度场和时间,λ表示导热系数,x和y表示厚度和宽度方向.
冷却过程中一冷区和二冷区用水量大小不同,导致其边界条件不同.
式中:hi单位为W/(m2K),W:瓦特,K:开尔文,表示二冷区中铸坯表面与冷却水之间第i段等效综合换热系数,Tw单位为℃,表示冷却水温度, Tb单位为℃,表示当前铸坯的表面温度.
其中i=1,2…,n,wi单位为W/m2,表示第i个冷却区冷却水的密度,α表示连铸机相关参数.
因为宽度、厚度边界条件对称,则可对称处理模型的计算区域——只计算横截面上厚度一半的区域,另一半即可对称得到,则在中心线上式(4)式、(5)式、(6)式成立.
式中:Tc为浇铸初始温度,Thick为连铸机厚度,Length为连铸机长度.
-
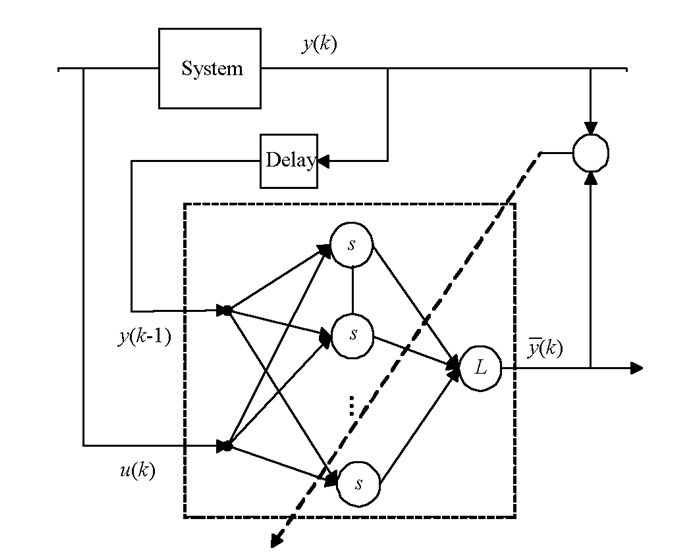
时滞BP神经网络是将实际系统输入和输出的过去值当作网络的输入,下一个时刻的输出作为输出信号.网络本身的结构依然是静态的BP神经网络,但是由于加入了延时输入就可以反映系统的动态变化过程(图 2).
该网络采用经典的三层BP网络,隐含层的阈值函数采用双曲函数,输出层的阈值函数采用线性函数.
如式(7)所示,k+1时刻系统的输出可以表示为历史输出和历史输入的函数,虽然这种网络本质上还是前向网络的结构,但是可以充分地反映系统的动态变化过程.
-
如果连铸凝固传热模型也可以用式(7)的形式表达出来,那么就可以使用时滞BP神经网络来描述连铸的传热过程.本文从机理模型入手将偏微分方程,即式(1)差分离散来推导出连铸凝固传热模型,也可以用式(7)的形式表示.首先对式(1)采用显式差分可得
其中令
$ a\frac{\lambda }{{\rho {C_e}}}$ 整理可得从式(9)可以得出显式差分求解偏微分方程的求解过程,即得知上一时刻温度场总可以求得下一个时刻温度场.
温度场T经过离散之后是一个矩阵,Tn+1表示第n+1时刻温度场,Tn表示第n时刻温度场.由此推知Tn+1与Tn存在如下关系
现在重点讨论位于边界上的点.对于处于x=0边界上的点而言,一般假设在x=0的外部还有一个虚拟的点,这个点依然满足控制方程,于是将i=0带入式(9)中可得
对边界条件式(2)采用差分离散可得
由此可得
将其代入到式(11)中消去虚拟点Tn-1j可得
由式(10)的启发可知,想要计算下一时刻表面温度,只需找到T0jn+1与T0jn的关系即可. Tw表示冷却水的温度在连铸过程中可以认为是常数,Δx,Δy,τ为空间步长和时间步长也可以视为常数.由式(14)分析可知,影响下一时刻表面温度的因素有当前时刻表面温度Tn0j,当前时刻边界条件h和当前时刻内部温度T1jn.连铸方坯内部温度变化较为缓慢,因此在这里假设T1jn也为常数.由此可以得到这样一个近似的关系.即已知当前时刻表面温度可以近似的计算出下一时刻表面温度.
结合式(14)与式(15)分析可知,T0jn+1仅仅只与T0jn,h,v有关.若将T0jn+1视为y(k+1),T0jn视为y(k),h,v视为u(k),得
由此可知连铸凝固传热模型可以表示为式(7)的形式,因此就可以使用时滞BP神经网络来对该机理模型进行近似.
本文所采用的时滞BP神经网络的输入为当前时刻表面温度T0jn,拉速v,冷却水量h,输出为下一时刻表面温度T0jn+1.由于二冷区每个冷却段的冷却水量各不相同,因此每个冷却区段采用一个独立的神经网络.
2.1. 时滞BP神经网络
2.2. 时滞BP神经网络实现连铸凝固传热模型
-
本文使用的数据是吗,某厂方坯连铸机数据,其中固相线温度TS=1 462 ℃,液相线温度TL=1 518 ℃,凝固潜热和比热分别为265.6 kJ/kg和Ce=540 J/(kg·K),
密度:ρ=7100,T < TS,kg/m3;
=7200,TS < T < TL,kg/m3;
=7300,T>TL,kg/m3;
其中:ρ表示密度,T表示二维温度场,TS表示固相线温度,TL表示液相线温度.
导热系数:λ=25,T < TS,W/m·K;
=30,TS < T < TL,W/m·K;
=55,T>TL,W/m·K;
某厂连铸机主要参数如表 1所示.
-
依照以上模型的参数,在ANSYS14的热力学计算模块中搭建出凝固传热仿真模型. ANSYS目前是世界上著名的有限元计算软件之一,广泛地应用于温度场,流场的计算,具有较高的可靠性.
本文分别以二冷区第一段和第二段为例子进行了仿真实验,将二冷区第一段离散了7个网格节点.神经网络隐含节点数的选择按照经验公式为
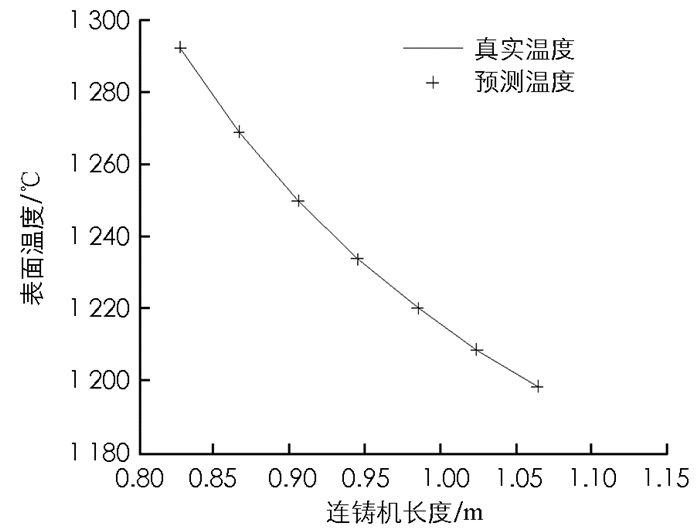
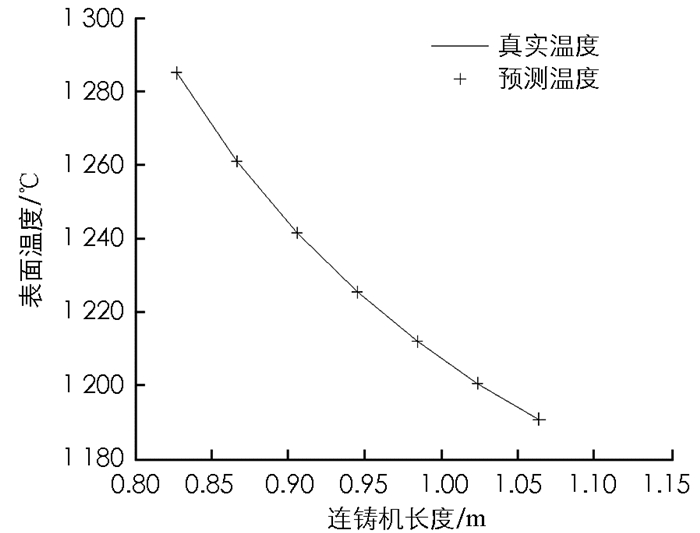
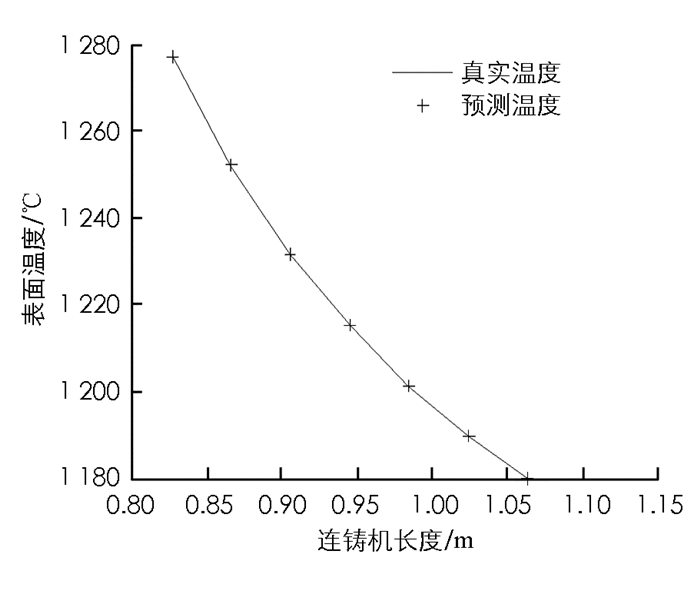
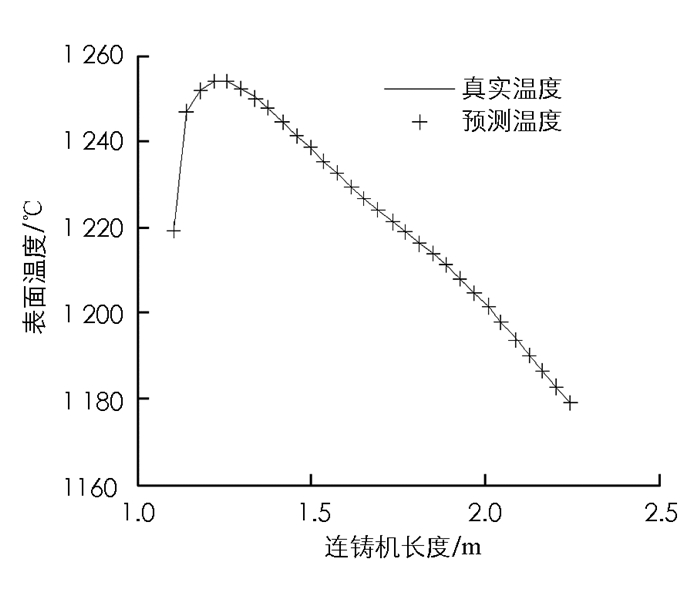
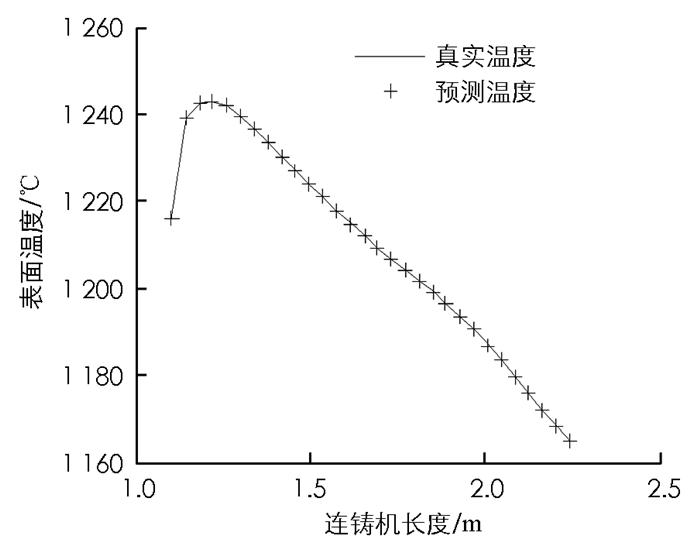
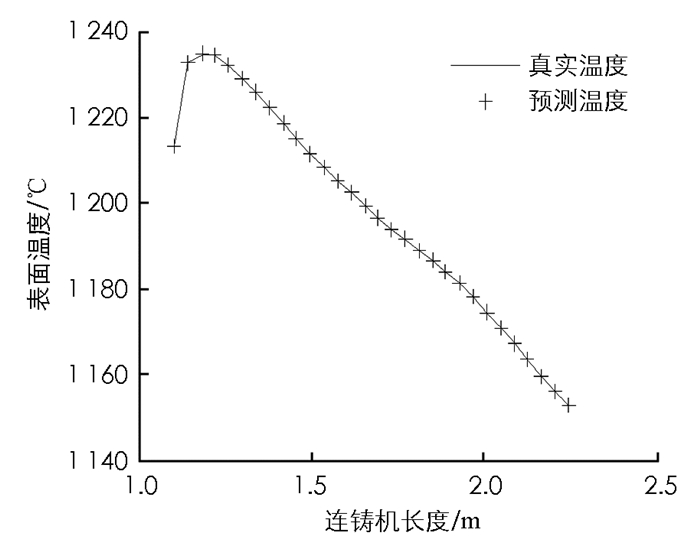
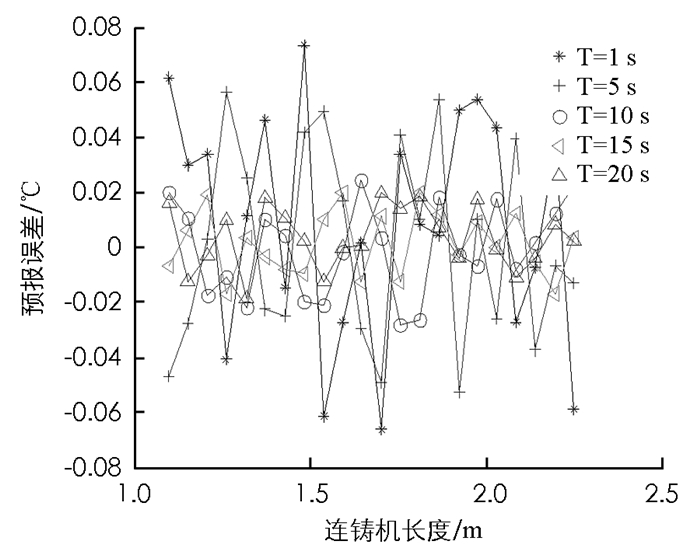
式(19)中n1表示隐含节点数,n,m分别表示输入向量和输出向量的维数,a是取0~10的常数.在二冷区第一段输入7个表面温度值、拉速和水量,所以n=9.输出是下一时刻的表面温度值,所以m=7,由此可以初步确定n1的范围为4~14.本文的仿真实验取n1=5.同理也可得出二冷区第二段隐含节点数的范围.本实验假设水量为线性变化,选取时间段为20 s的温度动态变化过程.现在分别将1 s,5 s,15 s,20 s的时刻温度真实值与测量值进行比较.
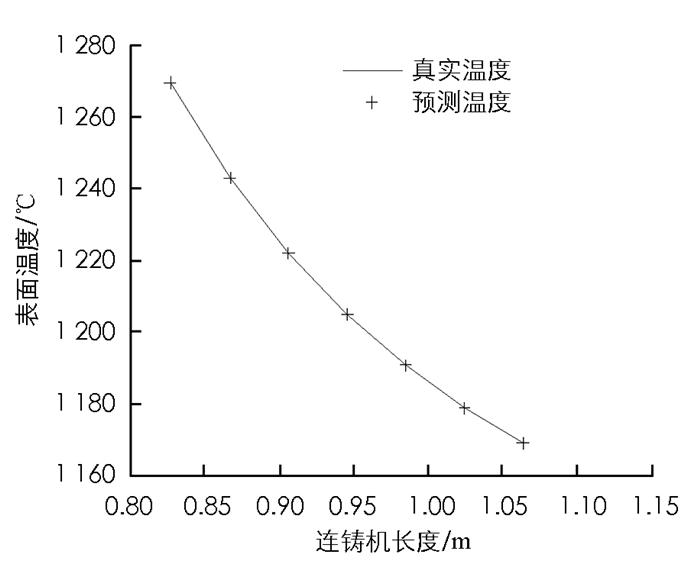
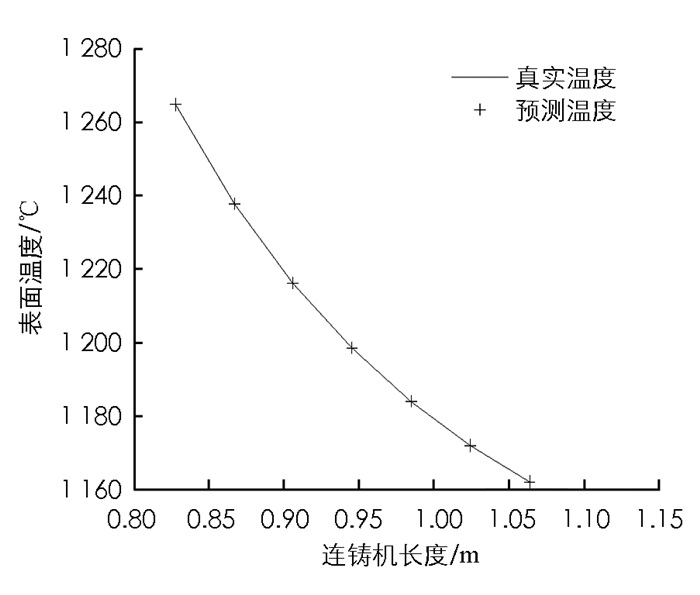
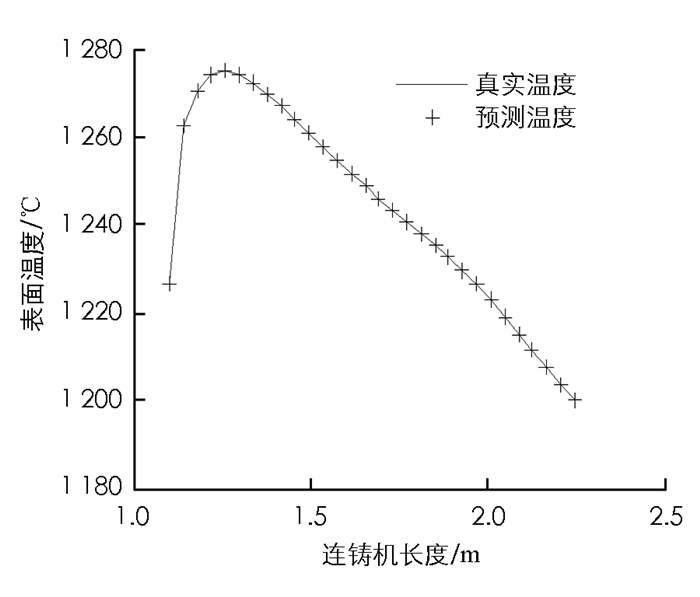
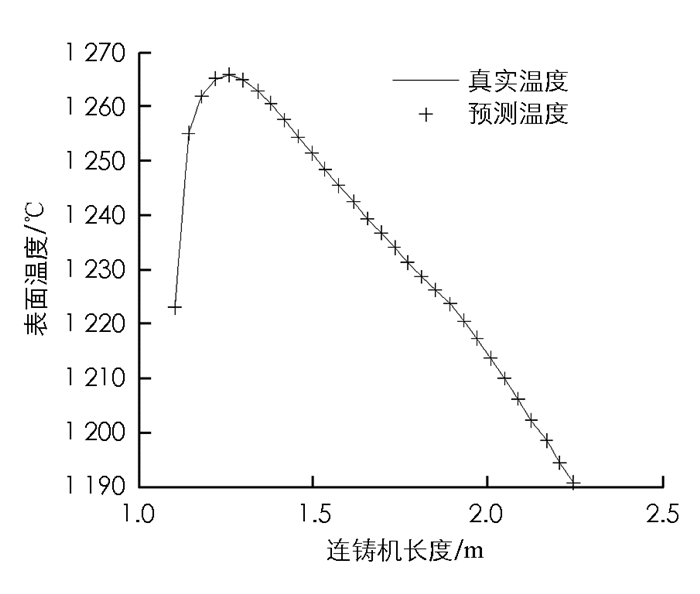
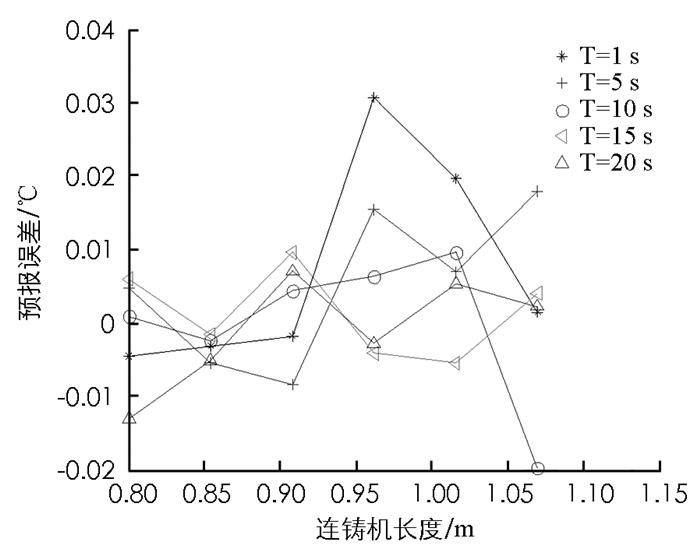
如图 3-图 7所示,二冷区第一段表面温度的预报最大相对误差为0.041%.由于二冷区第一段温度变化方式比较简单,所以从实验结果来看预报较为准确.如图 8-图 12所示,二冷区第二段表面温度的预报最大相对误差为0.089%.由于二冷区第二段神经网络输入输出维数增大,并且二冷区第二段存在回温现象,温度变化的方式比较复杂,所以给神经网络的预测造成了一定的困难.如图 13和图 14所示,二冷区第二段的预报误差要大于二冷区第一段的预报误差.
通过以上实验可以看出,时滞BP神经网络预测二冷区第一段与第二段的表面温度值和实际温度值均能很好地吻合.在对连铸方坯凝固传热模型特性充分认识的情况下,就能够合理地选择神经网络结构和参数,这样就能够达到较好的预报结果,实现快速准确地预报连铸方坯表面温度的目的.
另外,本文方法与二维有限差分法进行比较,具体铸坯表面中心温度预测值见表 2.
由表 2中数据可得出,本文方法预测值绝对误差在2.6%以内,而二维有限差法绝对误差在4%以内,本文方法在预测铸坯表面温度方面更接近实际值.
3.1. 某厂方坯连铸机的主要参数
3.2. 仿真实验结果与分析
-
本文在建立了连铸方坯凝固传热模型的基础上,通过时滞BP神经网络建立了连铸方坯二冷区铸坯表面温度预报模型,在理论上证明了该方法的可行性,并且以仿真实验验证了该方法的有效性,有效地克服了传统的传热模型计算不准确、计算时间长的缺点.本文接下来的研究方向是考虑建立一种能够快速准确地预报铸坯内部温度的时滞神经网络模型,以满足工业现场的实际需求.



 下载:
下载: