-
预应力撑杆钢柱由中心受压柱、撑杆和拉索构成,这类结构构件具有轻盈美观、建筑表现丰富、承载能力高等特点,由于这些特有的优点,预应力撑杆钢柱已在国内外被广泛应用[1],相关研究也逐渐开展.
Smith等人首先提出了预应力撑杆钢柱这种结构体系,并推导了其线性屈曲荷载计算公式[2]; Chan等通过非线性数值分析,研究了不同设计参数如初始缺陷、预应力、索截面积、撑杆刚度等对预应力撑杆钢柱稳定性能的影响[3]; Saito等对预应力撑杆钢柱的缺陷敏感性及相关屈曲进行了分析,提出了对这类结构构件进行非线性分析的新方法[4]; 舒赣平等对预应力撑杆钢柱进行了模型试验,考虑并分析了材料、柱截面、支座约朿和初始缺陷等因素对这类结构构件的影响[1]; Sera也通过模型试验验证了预应力撑杆钢柱优越的稳定性能[5].
然而现有研究主要围绕中心柱为圆管的预应力撑杆柱展开,而针对箱形截面预应力撑杆钢柱的研究却开展不多.事实上,当中心柱采用箱形截面时,预应力撑杆钢柱与其他构件的连接更为便捷.本文即是对采用箱形截面的预应力撑杆钢柱进行研究,通过屈曲分析考察不同参数对这类结构整体稳定性能的影响.
全文HTML
-
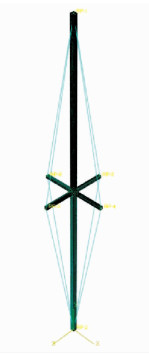
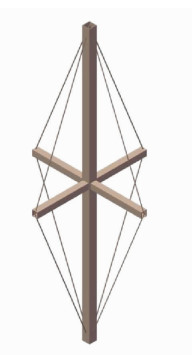
本文研究的预应力撑杆钢柱是由中心柱、撑杆和预应力索三部分构成.其几何模型如图 1所示,其中心柱采用截面形式为箱形的钢管.本文分析时中心柱长度设置为3 000 mm,拉索直径设置为4. 8 mm,而撑杆长度则包含150, 300, 450, 600 mm几种情况.在本文分析模型中,箱形截面中心柱的截面边长为40 mm,厚度为5 mm,采用符号40 mm× 40 mm× 5 mm表示此中心柱截面.与此类似,撑杆也采用箱形截面,截面厚度为5 mm, 截面边长包括20, 30, 40 mm 3种情况.
-
本文的数值分析采用有限元软件ABAQUS完成.为了提高有限元计算的精细度和准确度,分析时采用壳单元模拟中心柱和撑杆,而拉索采用不能受压的桁架单元模拟,柱和横撑杆采用钢材,弹性模量为206 000 N/mm2,拉索的弹性模量为160 000 N/mm2,分析中假定拉索处于完全弹性状态.本文研究的轴心受压预应力撑杆柱两端约束为铰接,图 2为其有限元模型示意图.
1.1. 几何模型
1.2. 单元和材料特性
-
为了保证后续数值分析结果的可靠性,本节通过比较数值分析和理论推导的结果以验证其准确性,验证模型的参数如表 1所示.在该验证模型中,拉索直径取为4.8 mm,弹性模量为160 000 N/mm2.
文献[6]推导了预应力撑杆钢柱屈曲荷载的计算公式,其表达式如式(1)所示:
式中Ncr,Ne分别代表预应力撑杆钢柱的屈曲荷载、普通中心受压柱自身的屈曲荷载. Kst,Ket分别代表等效平动弹簧刚度、普通弹簧刚度的临界值,可分别按式(2)、式(3)计算:
式中Es,E分别代表拉索和钢材的弹性模量,α为拉索与中心柱间夹角, As为拉索截面积,Ic代表中心柱的截面惯性矩,L为中心柱长.
表 2列出了预应力撑杆钢柱承载能力的理论和数值分析结果.可以看出,理论推导和数值分析结果的误差仅为4.88%.换而言之,采用数值分析的方法可以较为精确地获得这类结构构件的承载能力,这也是后文采用数值分析方法研究预应力撑杆钢柱稳定性能的前提[7].
-
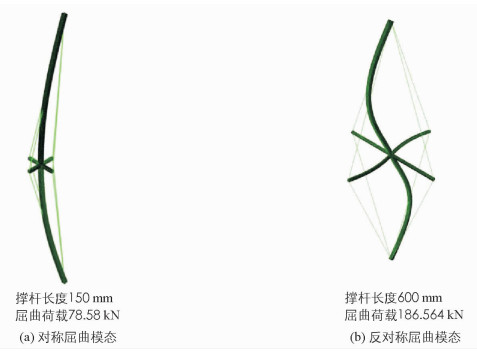
本节通过对预应力撑杆钢柱进行线性屈曲分析以研究其屈曲模态和屈曲荷载. 图 3所示为箱形截面预应力撑杆柱在轴心受压状态下的两类屈曲模态和屈曲荷载,其中图 3(a)和图 3(b)对应的撑杆长度分别为150 mm和600 mm.可以看出,随着撑杆长度从150 mm增加到600 mm,其屈曲荷载也由78.58 kN增加到186.56 kN,即增加撑杆长度可以显著提高其线性屈曲荷载,并将其屈曲模态由对称屈曲模态转变为反对称屈曲模态.
-
在上节的线性屈曲分析中没有考虑缺陷和几何非线性等因素对预应力撑杆钢柱稳定性能的影响,因而无法反映其实际性能.为此,本节对其展开非线性屈曲分析以进一步研究其整体稳定性能.在分析中,初始缺陷分布按照第一阶线性屈曲模态的变形形状施加.对于拉索中的预应力而言,本节按照文献[4]中的方式确定其大小.在本节的非线性屈曲分析中,重点考察撑杆长度、截面积以及初始缺陷大小等因素对这类结构稳定承载性能的影响.
1) 撑杆长度的影响
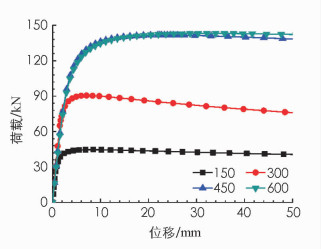
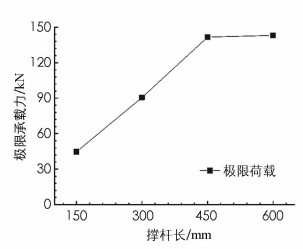
为了研究撑杆长度对轴心受压箱形截面预应力撑杆钢柱稳定性能的影响,本节对采用4种不同撑杆长度(150,300,450,600 mm)的预应力撑杆钢柱进行分析.分析时初始缺陷大小δ取为10 mm,撑杆截面为30 mm×30 mm×5 mm. 图 4所示为不同撑杆长度下预应力撑杆钢柱的荷载-位移全过程曲线,图中的位移为中心柱的轴向压缩.总体而言,增加撑杆长度可以提升预应力撑杆钢柱的承载能力. 图 5所示为不同撑杆长度下预应力撑杆钢柱的承载能力,可以看出,当撑杆长度不超过450 mm时,增加撑杆长度可以提升承载能力,然而,当撑杆长度超过450 mm时,增加撑杆长度却几乎不能进一步提升结构的承载能力.
2) 撑杆截面积的影响
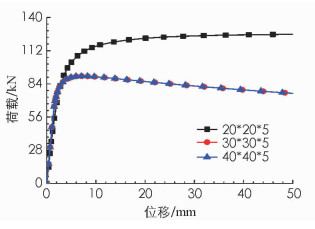
为了研究撑杆截面积的影响,本节分析时考虑了3种不同的撑杆截面尺寸,分别为20 mm×20 mm×5 mm,30 mm×30 mm×5 mm和40 mm×40 mm×5 mm.分析时撑杆长度固定为300 mm,初始缺陷δ为10 mm.
图 6所示为不同撑杆截面尺寸下预应力撑杆钢柱的荷载-位移全过程曲线.可以看出,撑杆截面为30 mm×30 mm×5 mm和40 mm×40 mm×5 mm对应的预应力撑杆钢柱承载能力相近,但二者均低于撑杆截面为20 mm×20 mm×5 mm对应的预应力撑杆钢柱承载能力.通过线性屈曲分析可以发现,当撑杆截面为20 mm×20 mm×5 mm时,预应力撑杆钢柱的屈曲模态为反对称;而当撑杆截面为30 mm×30 mm×5 mm或40 mm×40 mm×5 mm时,预应力撑杆钢柱的屈曲模态为对称屈曲.换而言之,当撑杆截面由20 mm×20 mm×5 mm变化为30 mm×30 mm×5 mm或40 mm×40 mm×5 mm时,预应力撑杆钢柱的屈曲模态由反对称屈曲变为对称屈曲.因此,在非线性屈曲分析中所施加的初始缺陷分布形状也由反对称变为对称,因而其承载能力反而降低.
3) 初始缺陷值的影响
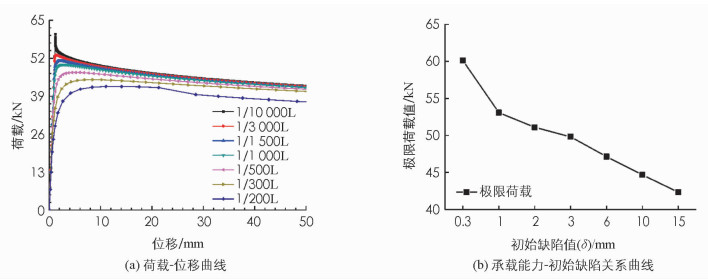
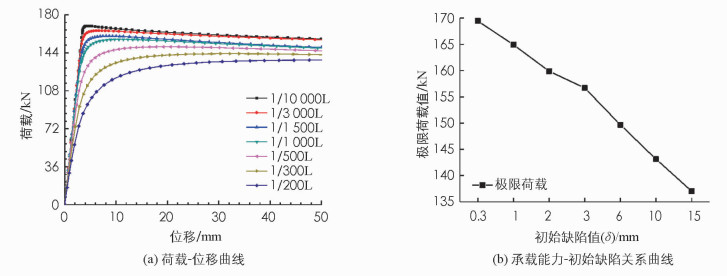
对于工程实际中的预应力撑杆柱,总是难以避免的存在初始缺陷.本节则是对箱形预应力撑杆钢柱进行缺陷敏感性分析,以考察初始缺陷大小对这类结构构件承载能力的影响.在本节的分析中,一共考虑了7种不同大小的初始缺陷,分别为L/10 000,L/3 000,L/1 500,L/1 000,L/500,L/300,L/200(其中,L为中心柱长)[8].分析中,撑杆截面尺寸定为30 mm×30 mm×5 mm,考虑了150 mm和600 mm两种撑杆长度. 图 7和图 8分别为撑杆长度为150 mm和600 mm时,预应力撑杆钢柱缺陷敏感性分析结果.由图 7可以看出,增加初始缺陷总是降低这类结构构件的承载能力,尤其是当初始缺陷较小时(δ小于1 mm).
值得注意的是,当撑杆长度为600 mm时,其承载能力与初始缺陷的关系却与撑杆为150 mm的情况有所不同.当撑杆长度为600mm时,承载能力随初始缺陷的增大而呈现出线性降低的趋势,如图 8(b)所示;而当撑杆长度为150 mm时,这种降低速度却呈现出先快后慢的特征,如图 7(b).
2.1. 模型验证
2.2. 数值分析
2.2.1. 线性屈曲分析
2.2.2. 非线性屈曲分析
-
1) 箱形截面预应力撑杆钢柱的屈曲模态可以分为对称和反对称屈曲,改变撑杆长度可使其呈现出以上两类不同的屈曲模态.当撑杆长度较短时,这类结构构件的屈曲模态为对称屈曲;当撑杆长度较长时,这类结构构件的屈曲模态为反对称屈曲.
2) 适当增加撑杆长度可以提升箱形截面预应力撑杆钢柱的承载能力,但是当撑杆长度过长时这种提升作用却不明显.
3) 增大撑杆截面尺寸并不总能提高箱形截面预应力撑杆钢柱的承载能力,过大的撑杆截面尺寸使得预应力撑杆钢柱的屈曲模态变为对称屈曲,此时其承载能力反而会降低.
4) 增大初始几何缺陷总会降低预应力撑杆钢柱的承载能力,但是这种降低作用却与撑杆长度相关.当撑杆较短时,承载能力随初始缺陷的增大呈现出先快后慢的降低趋势;而当撑杆较长时,承载能力则随初始缺陷的增大呈现出线性降低的趋势.



 下载:
下载: