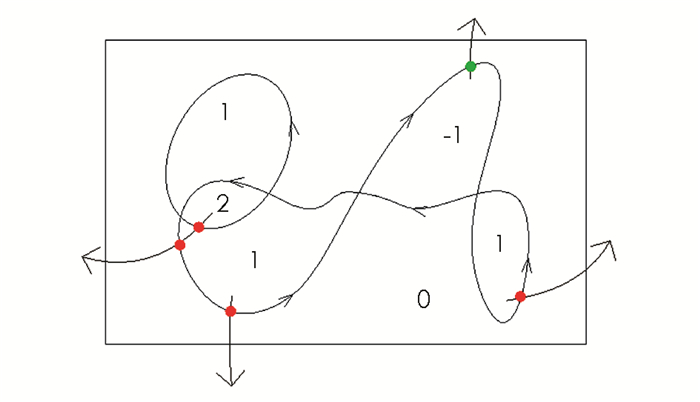
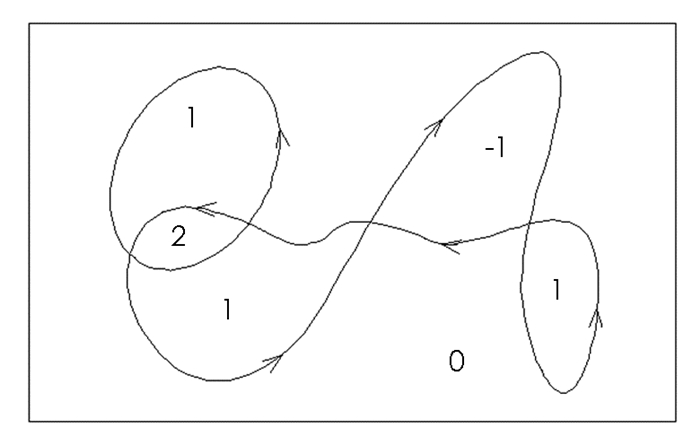
将轮廓看作二维欧式平面E2中的曲线，若曲线的终点与起点重合，则称曲线闭合，也称为循环.围绕点的环绕数被定义为循环绕逆时针方向传播的次数^[5].若环绕时曲线可以与自身相交，则进一步将环绕数概念扩展到具有有限数量曲线的平面上，区域的环绕数则被定义为所有循环的环绕数之和. 图 1是由2个闭合曲线产生的不同区域的环绕数.以环绕数为2的区域为例，2条曲线沿逆时针方向绕这个区域行进，则每条曲线的环绕数为1.

如果根据定义计算环绕数，则必须沿着平面中的曲线进行积分.然而，使用相交规则可以快速计算环绕数，如果一个循环从左边绕到右边（右边绕到左边），当越过它时，环绕数便增加（减少）1.

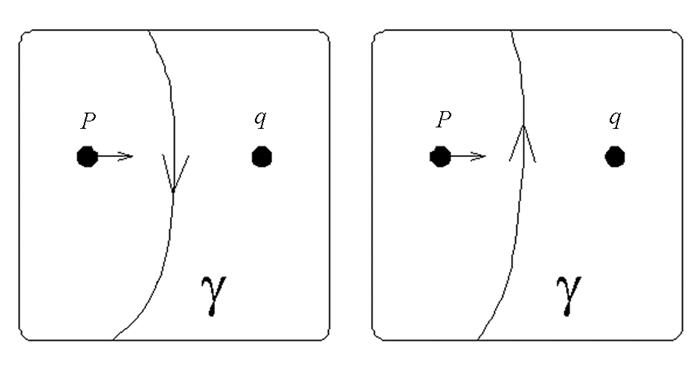
设wn_p，wn_q分别表示点p，q的环绕数，y_a表示a轮廓的二进制标记，穿越规则如图 2所示.

根据穿越规则，左图中wn_p=wn_q-1，右图中wn_p=wn_q+1. wn_p，wn_q分别是点p，q的环绕数.如果画出一条从点p到点q的路径，则环绕数之差的计算公式为

其中，L_pq和R_pq分别表示从右到左交叉的轮廓数与从左到右交叉的轮廓数.可以得出，环绕数仅由环路确定，无论路径如何，选择式(1)均成立.

如果预先确定平面中某些点的绕组数为0，例如，离任何曲线很远的点.然后，绘制一个任意路径从区域p的内部开始到该点，那么该区域的环绕数为

该方法如图 3所示.从一个点画一条任意的路径到图像的外面，环绕数值等于从右边穿过的轮廓减去从左边穿过轮廓的数量.

通过这种环绕数快速计算方法可以将区域标记与轮廓标记建立起对偶关系.作为对偶，一种属性便可以转换为另一种属性.例如，在平面上应用格林定理，画一条简单的约当曲线(闭合不自交)，则在二维区域上定义的许多量(例如面积)便可以通过一维曲线积分沿着轮廓进行有效的计算.

将环绕数快速计算的方法应用于具有二进制标签的区域场景中，并将重点放在前景轮廓检测上，将区域标记整合到基于比率的轮廓识别公式中，建立以轮廓显著性、区域相似度和轮廓平滑度为目标函数的能量最小化模型，便可以通过线性规划有效地解决图像前景目标识别问题.

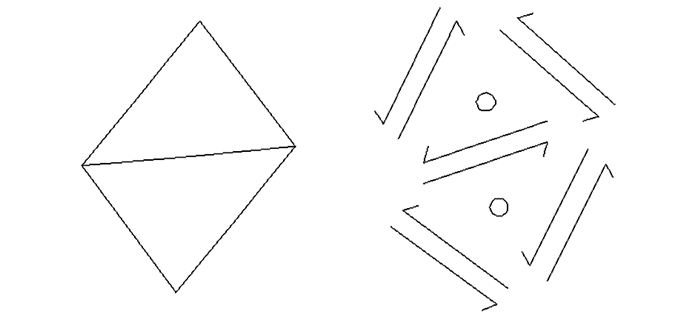
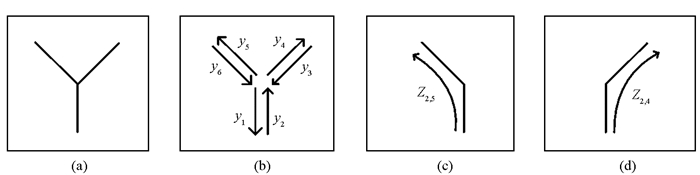
图像的亮度、纹理或颜色变化等因素均会引起图像轮廊的变化^[6].本文主要研究场景中突出目标部分的轮廓识别.相关实验表明，一个显著物体的轮廓与希望目标的轮廓不同时，很难有效地从纹理轮廓中来区分它们^[7].对此，本文将目标轮廓提取问题转化为区域和轮廓的能量最小化问题.选择超像素分割方法解决轮廓和区域能量最小化问题.每个超像素表示图像中最基本的区域，则每个超像素的边界被线性分为多个轮廓元素. 对于每个元素，引入互为共轭的2个相反方向的(双向)轮廓.如图 4所示，2个三角形产生2个区域和外侧8条有向边.左图显示2个三角形区域及其轮廓，右图显示从图像轮廓和区域提取的情况. 2个圆圈表示2个区域标记，箭头表示轮廓标记.

令变量x={x_i|i=1，2，…，N_r}表示共轭边中的正向边N_r的二维标记，y={y_j|j=1，2，…，N_e}表示共轭边中的反向边N_e的二维标记.引入环绕数概念研究二维目标与背景的分割问题，轮廓标记的标记集合表示为Y={0，1}N_e，区域标记的标记集合表示为X={0，1}N_r.

采用能量函数E(x，y)表示图像的背景对比度和轮廓平滑度等标记，则能量最小化模型可表示为

为确保约束拓扑的正确性，通过建立轮廓连续性约束、环绕数约束以及曲率项约束来保证能量最小化模型的有效性.引入约束后的能量最小化模型为

其中，s.t.是约束条件；ΦC(x，y)是轮廓连续性约束，表示为

其中，j属于顶点集V中的任意值，j_in和j_out分别是靠近顶点j与远离顶点j的拓扑指数.依据每个顶点的净流量为0建立约束.由于流体网络没有源节点与终节点，故所有的流均可以被分解成一个循环.因此，本文的方法旨在提取一组闭合曲线作为轮廓.

约束集W表示区域标记与轮廓标记一致性的环绕数约束，将活动轮廓的相邻(即入射)区域具有不同的区域标记作为一致性条件，如果2个相邻的区域具有不同的标记，则其中的一个轮廓元素必须处于活动状态.此条件保证了每条边必须是区域轮廓的一部分，并且每个区域都被轮廓包围.

其中，x_i和y_j表示2个相邻区域的标记；G表示区域所在无向图；变量y_m和y_n表示这2个区域的2个共轭边.如果其参数为真，则函数f等于1，否则等于0.

若假设每个图像都被矩形边框包围，图像之外的任何区域标记均为0，则区域i的环绕数为

其中，P_i和N_i分别是从右到左交叉以及从左到右交叉的轮廓.

式(7)中所有超像素都可以表示为以下环绕数约束，且满足式(4)中约束集W的条件：

其中，M是元素为0，1或-1的矩阵.例如取M的第i行，M(i，α)=1，∀α∈P_i；M(i，β)=1，∀β∈N_i；其余元素为0，则这些约束的数量与超像素的数量相同.

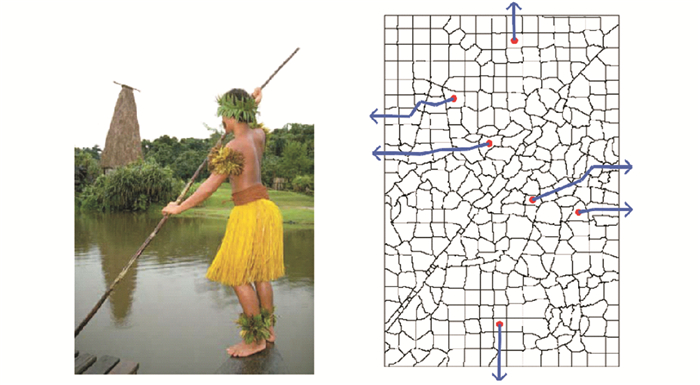
理论上的环绕数约束不依赖于从每个超像素到图像外部路径的选择，然而，实际应用中在连接点附近可能难以确定邻接关系.为了将错误风险最小化，本文采取深度优先搜索遍历算法^[8].从图中任意一个顶点出发，首先，访问此顶点；然后，依次从没有被访问的邻接点出发，按深度优先的顺序遍历整个图，直到图中所有有路径相通的顶点都被访问到；若此时图中还有顶点没有被访问过，则另外选择图中一个没有被访问的顶点作起始点，重复以上过程，直到图中所有顶点都被访问到.从中选择一条路径，使得该路径上的区域总数最小，则减少了环绕数计算的次数.穿过该路径的轮廓最长，则增加了计算的可靠性，实现最优.具体实施如图 5所示.

由于区域标记由轮廓标记线性决定，所以环绕数约束可以限制可行区域标记的集合.如果区域标记是二维的，假设轮廓彼此不相交，并且每个轮廓仅与2个区域相邻，将轮廓分成较小的部分.对于标记为1的超像素，定义其相邻边沿的逆时针方向为有效方向，区域轮廓到其他区域的环绕数为0.由于轮廓不被多于2个区域共用，因此可以对每个超像素进行此操作，而不会发生冲突.对于任何区域标记只能为0或1的分割，总是存在一组定向边界，使得区域标记等于由这些边界产生的环绕数，从而保证了区域标记与轮廓标记的一致性.

人类视觉系统倾向于将平滑轮廓组合在一起^[9].本文提出的方法考虑增加轮廓平滑度.轮廓的平滑度可以通过曲率平方的积分来表示.让P_E表示共用一个顶点的所有对应轮廓的集合，令z={z_ij|(i，j)∈P_E}表示所有结点N_j，Z={0，1}N_j是所有结点的集合.

建立连接模型如图 6所示，图 6(a)显示了图像中检测到的一个结点；图 6(b)显示了6个表示相关轮廓的变量；图 6(c)，6(d)显示2个活动轮廓.

为了确保结果的有效性，对连接点进行了约束，表示为φ_J(y，z)≤0.首先，每个有效轮廓应该形成至少一条尾部与当前轮廓相连接的曲线；其次，每个邻接变量仅在2个相关轮廓均处于活动状态时才有效.连接点约束可由线性不等式表示.

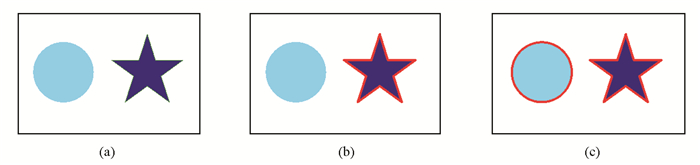
图 7是增加曲率项前后的目标轮廊提取效果，图 7(a)是输入图像，星形图案的轮廓和区域由于背景对比强烈而被标记.缺少曲率项的模型仅可以提取图 7(b)所示的星形轮廓，当加上曲率项时，则得到如图 7(c)所示的图形，即可同时提取到圆形轮廓与星形轮廓.

将拓扑领域中的环绕数概念引入轮廓识别中，结合轮廓连续性约束、曲率项约束对能量最小化模型进行约束，为区域轮廓标记一致性条件提供了一种有效的解决手段，保证了能量最小化模型的拓扑正确性.

本文采用比率能量函数对所提出算法进行应用分析，比率能量函数具有计算复杂度低、优化效果好等优点.有效避免了传统的归一化分割等方法中存在的对大尺度的图像进行处理时，计算过于复杂且参数的选取对划分稳定性影响较大的问题.因此，将比率能量函数作为对象，以证明所提的环绕数约束算法的有效性.

轮廓间隙和前景区域的比率为

测量总间隙长度的轮廓项为

其中，v_i是轮廓i的间隙长度.

其中，a_i是区域i的面积.

针对式(10)中比率能量函数在物体内或背景中可能存在明显的分散轮廓的问题，添加区域相似项E_R以改善这种噪声的影响.新的目标函数定义为

其中，区域相似项E_R(x，y)表征图像和背景超像素之间的相似程度.

式中，P_R表示距离小于阈值的像素对；w_ij由区域i和j之间的颜色特征差异程度确定.将区域标记和轮廓标记定义为二进制，则基于比率的分割模型为

其中，标记空间为X={0，1}N_r，Y={0，1}N_e. N_r是共轭边中的正向边，N_e是共轭边中的反向边.

曲率标记定义为

其中，曲率系数u_ij是沿着2个轮廓的曲率平方之和；参数a_c是整体曲率项的权值，a_c的取值控制识别目标轮廓的平滑程度，取值范围为[0, 1]，图 8为a_c取不同值时的效果图.依图可知，当a_c=0.1或者1时，其分割精度不佳，存在漏分割现象；当a_c=0.5时，其分割精度较为理想，准确地获取了完整的飞机轮廓.

因此，联合式(15)与式(16)，可得引入曲率标记后的比率分割模型为

通过将轮廓标记、区域相似性标记以及曲率标记融合，得到最终形式的基于比率的分割模型.根据式(12)可知，分母A(x)恒为正值，则证明能量函数(17)在图像G中为凸的，此时，只需证明f(x，y，z)=E_R(x)+E_B(y)+E_C(z)为凸函数.对于E_R(x)项，在图像G中，对于任意给定值x_i=x_i^*，x_j=x_j^*，且∀a_r∈[0, 1]，根据式(14)，有∀x_j^*≥∀x_i^*+▽(x_i^*)Ta_r(x_j^*+x_i^*)成立；E_B(y)项中，∀a_b∈[0, 1]，满足|▽(a_bv_i+a_bv_j)²≤a_b(|▽v_i|²+|▽v_j|²)成立；E_C(z)中，根据式(9)，有a_c(z_ij+y_j)²≤a_cz_ij²+a_cy_j²成立，则能量函数式(17)为凸函数，存在最优解.随后，通过调节其中的轮廓项权值a_b、区域相似项权值a_r、以及曲率项权值a_c，便能够精确地对目标轮廓进行识别，根据权值a_b，a_r和a_c的较优组合，输出式(17)的最小值，也就是较优值.其中，a_b取值越小，则识别目标与背景间差异越明显. a_r的取值反应滤除识别目标与背景间噪声强度，a_r取值越大，滤除噪声效果越强.

为了确定式(17)中的权值a_b，a_r和a_c的最佳组合，本文采用如下算法：首先设定k=0，令a_b=a_r=a_c=1为能量函数初始值，预先给定一个迭代次数N₁>0和误差限度δ>0.对于第k次迭代，固定a_b，a_r，改变a_c，求取式(17)的极小值；固定a_b，a_c改变a_r，求取式(17)的极小值；再固定a_r，a_c，改变a_b，求取式(17)的极小值.然后判断$\frac{\left\|\left|f^{k+1}\right|-1\right\|}{\left\|f^{k+1}\right\|} \leqslant \delta$是否成立，若成立，则停止迭代.从而求解出轮廓项a_b、区域相似项a_r以及曲率项权值a_c.在本文中，通过对多幅图像进行测试，取a_b=1，a_r=1，a_c=0.5时，可使算法性能较优.

为了验证本文目标轮廓识别算法的有效性与优异性，利用MATLAB软件对其进行测试，并采用Weizmann Horses与Weizmann Segmentation这2个标准数据集来测试本文提出的算法与超像素算法(SC)^[10]、比例分割算法(RC)^[11]、Ncuts算法^[12]、GPAC^[13]算法的目标轮廊提取效果. Weizmann Horse数据集包含328幅复杂的马类图像，描述了自然环境中马的侧面形态，并且附带有人工标记的真实值，适用于对图像轮廓识别算法的性能进行测试；Weizmann Segmentation数据集包含200幅原始自然图像，其中单目标图像和双目标图像各100幅，该数据集还提供了对应的灰度图像以及人工分割的图像进行参考.实验关键参数设置为：a_b=1，a_r=1，a_c=0.5.

如图 9所示，虽然Weizmann Horse数据集中的马很明显，但由于马的颜色、纹理等特征差异较大、身体姿态各异，给算法的设计带来了很大的挑战.例如，马背和马身体内部有明显的轮廓，由于对比度低，容易造成轮廓缺失^[14]，所以采用区域标记和轮廓标记融合有助于获得更清晰的轮廓.

为了证明本文所提算法的有效性，对本文算法与传统算法进行了比较.本文选取与文献[15]相同的F测度评价标准，随机选取训练图像，并对样本训练数量(n)与识别准确率(F)进行定量分析，通过对比初始分割图像的掩模与真实数据的掩模进而计算F值，仅当识别到的轮廓接近目标真实轮廓时，F值接近100%. F测度的计算公式为

其中，P，R分别表示精确度和召回率；t表示返回的有效样本数量；k表示返回的样本数量；n表示样本训练数量.

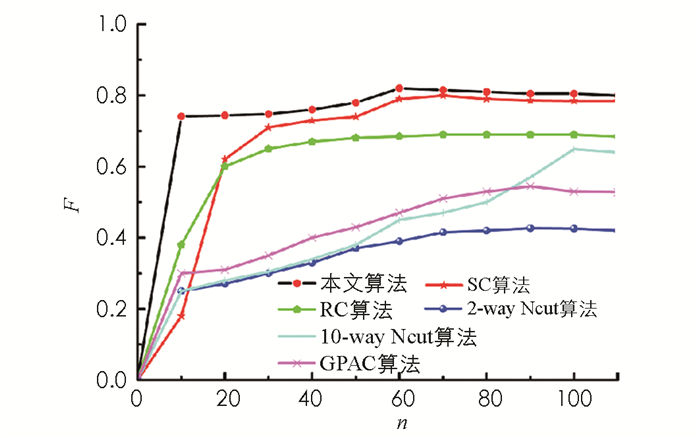
基于Weizmann Horse数据集进行实验，不同算法的F值测试结果如图 10所示. SC算法在n=70时，根据式(18)计算得到的F值理论值为78%；RC算法在n=70时，F值可达到69%；Ncuts算法n=90时F值可达42.7%；GPAC算法在n=90时F值可达54.5%；本文提出的环绕数约束法在n=60时，识别准确率高达80.2%.这表明本文提出的环绕数约束法对该数据集有效.

随后，根据所提算法与对照组技术的最优F值进行轮廓识别测试，结果见图 11.依图可知，在SC算法的输出结果中，马腿通常作为整体区域进行连接；RC算法容易产生假轮廓(例如天空和草地)，Ncuts算法只能分割部分目标区域；GPAC算法容易将部分背景区域误识别为目标.而本文算法的轮廓识别精度最佳，没有分割背景等伪信息.这些结果表明，环绕数约束法能更好地将马与背景进行分割.

Weizmann Segmentation数据集中图像目标物体与背景间存在灰度值和纹理的模糊性，使用传统的轮廓识别算法很难准确识别^[16].为进一步改善轮廓识别效果，针对Weizmann Segmentation数据集进行的实验中引入曲率标记，增加轮廓平滑度.

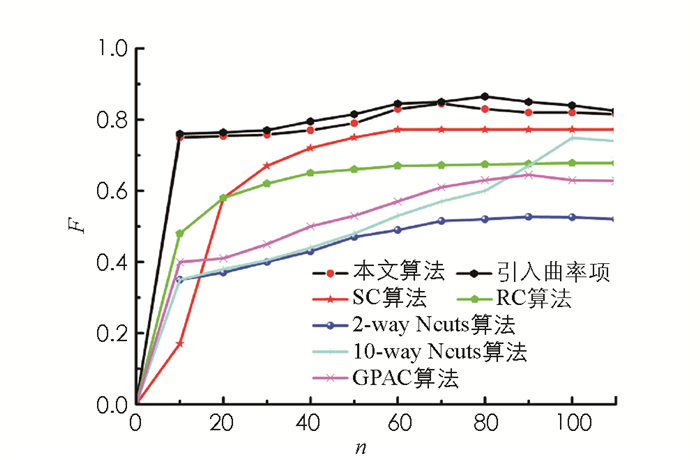
基于Weizmann Segmentation数据集进行实验，不同算法的F值测试结果见图 12.由图可知，本文提出的环绕数法在仅采用轮廓标记和区域标记，而不考虑曲率标记的情况下，其最优F值可达到84.5%，引入曲率标记后能进一步提高F值到86.5%，均优于其它传统算法.这表明将环绕数约束法引入曲率标记后识别效果更佳.

同样，根据所提算法与对照组技术的最优F值进行轮廓识别测试，结果见图 13.依图可知，在SC算法的输出结果中，由于算法的非凸性，容易产生局部收敛甚至发散，使其分割不完整；RC算法分割时所包含的语义信息较少，所以分割效果不够理想，容易产生假轮廓(例如天空和草地)，Ncuts算法由于其对图像边界的贴合性较差，只能局部均匀的分割背景区域；GPAC算法分割结果更倾向于具有相同的类内相似度，容易将背景与目标相似区域误识别为目标.而本文算法引入曲率标记后能更好地将目标与背景进行分割.

针对当前图像轮廓识别算法中，由于区域标记和轮廓标记性质不同导致难以实现多标记融合识别，识别效果不佳的现象，本文提出了一种基于能量最小化模型的环绕数约束法的图像分割方法.该方法简单实用，基于能量最小化模型的环绕数约束法只涉及一组线性约束，确保了区域标记与轮廓标记的一致性.与传统的图像处理方法相比，采用轮廊标记与区域标记融合技术进行图像处理，具有更好的效果，优势明显.