考虑下面有N个关联子系统的不确定离散时滞大系统

其中：$\boldsymbol{x}_{i}(k) \in \mathbb{R}^{n_{i}}$是系统状态；$\boldsymbol{u}_{i}(k) \in \mathbb{R}^{m_{i}}$是控制输入；正整数h_ij代表系统时滞，$h = \mathop {\max }\limits_{i,j = 1,2, \cdots ,N} \left\{ {{h_{ij}}} \right\}$；ψ_i(k)是定义在[－h，0]上的初始状态；A_i，B_i和A_ij是具有适当维数的常数矩阵；ΔA_i(k)，ΔA_ij(k)是代表时变不确定性的未知矩阵.对系统(1)做如下假设：

假设 1    B_i是列满秩的.

假设 2     (A_i，B_i)是可控的.

对系统(1)，存在非奇异变换$z_{i}(k)=\boldsymbol{T}_{i} \boldsymbol{x}_{i}(k)(i=1, 2, \cdots, N)$使系统(1)等价于

其中

由式(2)-(7)，得到

由B_i列满秩，易知不确定性ΔA_i2，ΔA_ij2满足匹配条件

其中ΔL_i2(k)，ΔM_ij2(k)满足

其中L_i2和M_ij2是常数.

假设非匹配不确定性ΔA_i1(k)，ΔA_ij1(k)满足

其中D_i，E_i，D_ijd和E_ijd是具有适当维数的已知常数矩阵，E_i，E_ijd满足

F(k)是未知的时变矩阵函数，满足

对不确定离散时滞大系统(2)，选择如下滑模面

其中c_i1，c_i2具有合适维数.选取c_i使得(c_iB_i)是非奇异的，从而滑模面s_i(k)是稳定的^[12].

到达条件如下^[13]

其中S(k)=[s₁(k)，s₂(k)，…，s_N(k)]^T.

引理 1^[13]     对任意的$ \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}} \in \mathbb{R}^{n}$和矩阵函数F(k)满足

不等式

成立

定理 1     对不确定离散时滞大系统(1)，选取如下控制器，则系统状态在有限时间内到达滑模面

证     由s_i(k)沿系统(2)的前向差分，易知

其中

由式(9)，(10)，(11)和(14)，并利用引理1，得到

由控制器(12)和式(13)，(15)易知

其中k_i1，k_i2是常数并满足k_i1>0，k_i2>0(i=1，2，…，N).

考虑形如式(8)的不确定时滞大系统，其中

时滞和初始条件如下

并有

选取$c_{1}=\left[\begin{array}{ll}{0} & {1}\end{array}\right], c_{2}=\left[\begin{array}{ll}{0} & {\frac{1}{2}}\end{array}\right], \boldsymbol{c}_{3}=\left[\begin{array}{ll}{0} & {\frac{1}{3}}\end{array}\right]$，得到$E_{1 a}=0.4, E_{2 a}=0.09, E_{3 a}=0.1, E_{12 \alpha d}=0$，$E_{13 a d}=0.12, E_{21 a d}=0.04, E_{23 a d}=0.15, E_{31 a d}=0.04, E_{32 a d}=0.08$.

设计变结构控制器(12)，系统状态的仿真图如图 1-3.

从图 1-3可看出，系统状态是渐近稳定的.

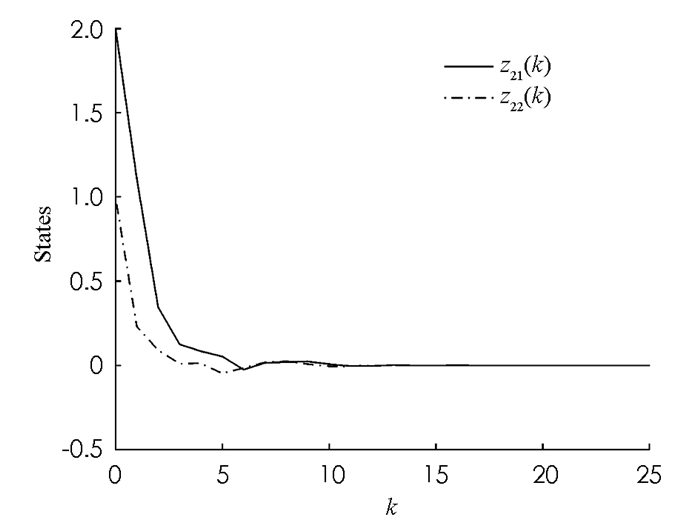
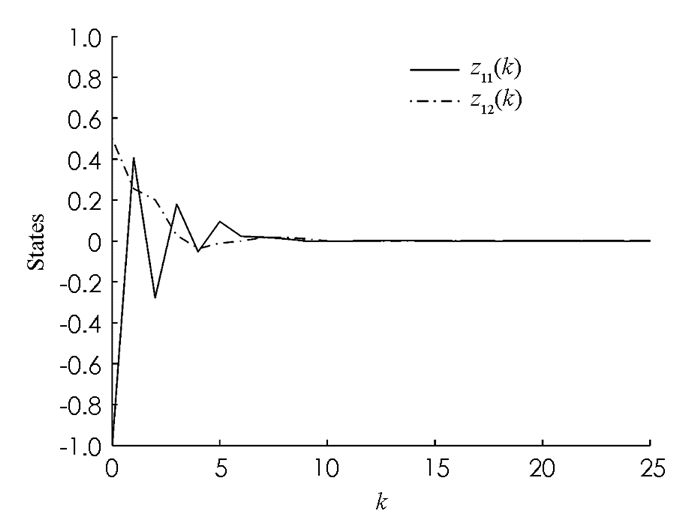
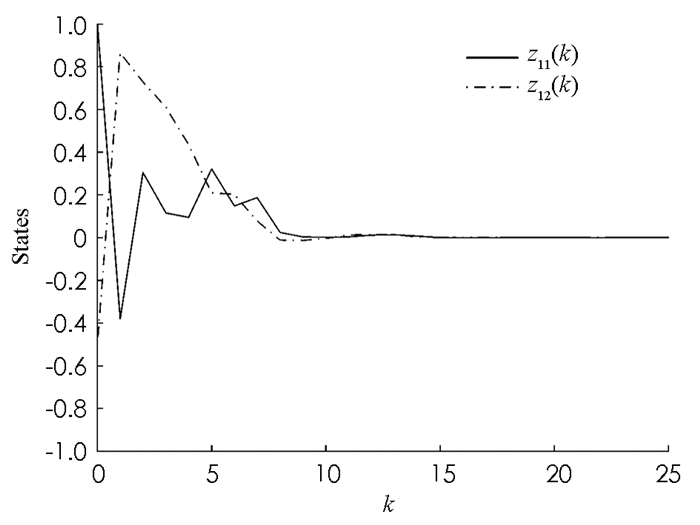
本文研究了具有非匹配不确定性的离散时滞大系统的变结构控制问题.设计了系统的变结构控制器，使系统状态在有限时间内到达并保持在滑模面上.与传统变结构控制设计相比，克服了不确定性满足匹配条件的缺点.最后，仿真算例说明了该方法的有效性.