-
在漫长的农业社会中, 国家经济的发展与土地资源、劳动力数量(即农业人口数量)密切相关[1].随着全世界逐步迈入工业社会, 大多数国家逐渐发展为工业国, 国家经济的发展开始取决于工业规模和工业劳动力的数量[2].目前, 国家经济的发展则日益依赖于信息技术、网络技术、通信技术等高科技产业, 高科技人才、高素质人才的数量成为各国经济实力比拼的关键所在[3-4].在相当长的一段时间里, 一个国家的教育似乎与本国经济发展之间缺乏必要的关联性.然而, 在21世纪乃至以后, 教育尤其是高等教育将成为国家经济发展的决定性因素[5].因为, 教育尤其是高等教育直接决定着一个国家高科技人才、高素质人才的数量和质量, 那些高等教育水平高的国家必将成为新时代中的经济强国乃至世界经济的领跑者.周茜等[6]认为, 经济的合理发展体现为各种资源的协调, 更决定于各类人才的协调, 要推动国家经济的发展必须大力发展高等教育, 而高等教育的发展又依赖于充分的经济投入, 二者是协同关系.丁三青[7]指出, 高等教育和经济发展之间, 通过人才这一要素形成了共轭效应, 这是对二者协同发展理论的进一步升华. Dockery等[8]通过研究发现, 在一个国家之内, 各地区之间教育水平的差异性会导致地区经济发展水平的巨大差距.胡德鑫[9]引入道格拉斯投入产出模型, 将高等教育看作投入, 将经济发展看作产出, 分析了二者之间的关联关系.樊星等[10]利用中国各个省份的面板数据, 从时间和空间2个角度分析了高等教育对中国各地区经济发展的贡献程度.李毅等[11]以中国中部地区为研究对象, 依托DEA数据包络模型, 分析了中部6个省份高等教育和经济发展关系.崔玉平等[12]以黑龙江省为研究对象, 采用CES模型分析了该省高等教育对经济发展的促进作用.本文在前人研究成果的基础上, 将一种性能更为优秀的神经网络RBF网络引入进来, 依托中国高等教育和经济发展的宏观数据, 分析二者之间的关系.
全文HTML
-
在分析两类数据之间隐含的关联关系时, 神经网络是一种比较理想的方法, 将两类数据分别看作神经网络的输入和输出代入神经网络, 训练并直到网络达到稳定, 二者之间通过隐含层表现出的权重关系, 就体现了二者之间的关联关系.
RBF网络也称径向基神经网络, 相比于一般的神经网络它具有更加优秀的局部逼近性能, 而且隐含层某个局部确定后, 新局部结构的确定只需要少量的调整即可实现, 这就使得RBF网络的局部学习性能非常理想, 不仅逼近准确而且学习速度快.RBF网络的非线性性能也是非常理想的.
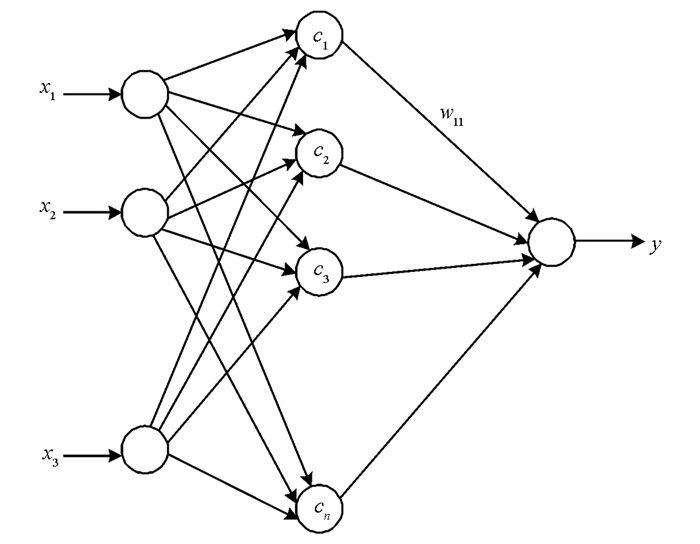
同大多数神经网络一样, RBF网络也包含3个层次, 即输入层、隐含层和输出层.一个典型的RBF网络结构如图 1所示.
在RBF网络中, 输入层神经元到隐含层之间的关系体现为非线性, 而隐含层到输出层神经元体现为线性, 输入到输出的关系最终体现为2种特征的综合效果.最终的输出计算如下:
这里, 参数xj用于表示径向基网络的各个输入神经元; 参数ck用于表示隐含层各个径向基函数的中心矢量; 参数wik用于表示各个隐含层神经元对输出神经元的权重; 参数y用于表示径向基网络的输出; 参数Φ用于表示径向基函数, 它在不同情况下又有不同的表现形式, 如高斯函数形式、样条函数形式、二次函数形式等等.
-
在本文的实证研究工作中, 借助RBF模型, 对我国高等教育和经济发展的关系展开研究.根据投入产出经济关系分析, 影响经济的要素有很多, 如劳动力投入、资本投入、科学技术水平的发展等等.在本文中, 主要考虑和高等教育相关的因素对于经济发展的影响.
为了给RBF网络输入和输出配置对应的参数, 选取4组变量, 分别是变量B, 从2000-2017年我国历年的本科生招考人数, 单位万人; 变量Y, 从2000-2017年我国历年的研究生招考人数, 单位万人; 变量J, 从2000-2017年我国历年的高等教育投入经费, 单位亿元; 变量G, 从2000-2017年我国历年的GDP总量, 单位亿元.
在上述4个变量中, 变量B、变量Y、变量J代表了我国高等教育的规模和投入水平, 变量G代表了我国经济发展的水平.其中, 变量B、变量Y、变量J作为RBF网络的输入神经元, 变量G作为RBF网络的输出神经元, 将4个变量代入RBF网络进行训练, 网络达到稳定后, 得到的权重就反映了高等教育和经济发展之间的关系.
从2000-2017年4个变量的原始数据及取对数的结果如表 1所示.
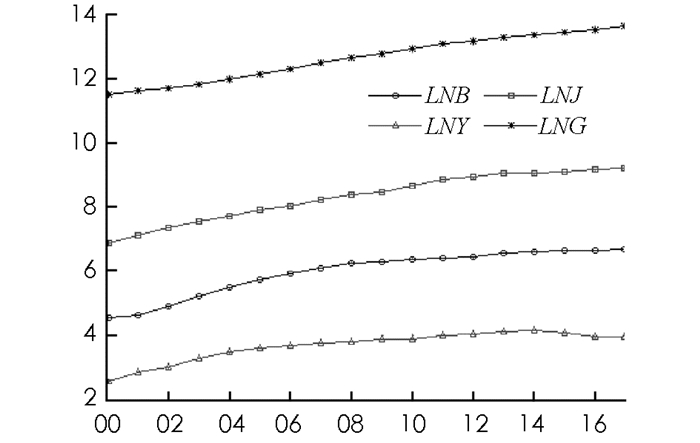
表 1中, 变量B、变量Y、变量J、变量G的原始数据因为单位不同, 在数值范围上存在很大的差异, 为了消除这种差异对迭代收敛稳定性的影响, 进一步取4个变量的对数结果, 得到4个新的变量, 即变量LNB、变量LNY、变量LNJ、变量LNG, 新的变量对比曲线结果如图 2所示.
从图 2中可以直观地看出, 从2000-2017年间, 我国的GDP总量不断增加.相应地, 高等教育投入经费和本科生、研究生的招考数量也不断增加, 表现出与GDP相同的态势. 2015年以后, 因为高等教育招生规模趋于饱和, 尤其是研究生招考趋于饱和, 研究生的数量开始下降, 而对应的GDP增速也有所放缓.
将上述数据分别代入图 1所示的RBF神经网络进行训练, 在520次迭代以后网络趋于稳定, 提取此时从输入到输出的权重, 结果如下:
变量LNB——〉变量LNG的权重wBG=0.23;
变量LNY——〉变量LNG的权重wYG=0.45;
变量LNJ——〉变量LNG的权重wJG=0.32.
经RBF网络模型的分析结果显示, 本文遴选的有关高等教育的3个变量, 对于经济发展都存在正向影响, 并且研究生的招考数量对于经济发展的影响最大, 权重达到了0.45;其次是高等教育的经费投入, 权重为0.32;最后是本科生的招考数量, 权重为0.23.
从近18年的实际数据来看, 高等教育对于我国经济发展存在明显的促进作用, 尤其是高端人才(研究生)的培养数量, 其促进作用更大.
-
在新的经济发展形势下, 世界各国都更加重视对高科技人才、高素质人才的培养, 也更加重视对高等教育的投入.越来越多的理论研究显示高等教育对经济发展存在促进作用.本文在这样的背景下, 引入RBF模型, 将高等教育规模和投入水平作为输入, 将经济发展水平作为输出, 对高等教育和经济发展之间的关系进行分析.遴选了从2000-2017年我国本科生招考数量、研究生招考数量、高等教育投入经费、GDP总量作为实证研究的基础数据, RBF网络的分析结果显示, 高等教育对于我国经济发展起到明显的促进作用, 尤其是高端人才的培养促进作用更加明显.



 下载:
下载: