-
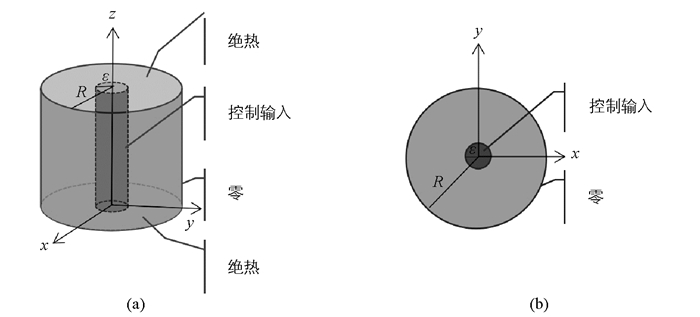
本文考虑固态化学反应或生物发酵材料的温度稳定问题.工程上,装材料的容器一般为圆柱体.如果控制器设置在圆柱体的上下面,侧面绝热,那么其温度的控制由1维反应扩散方程的边界控制模型描述[1-2].如果控制器设置在圆柱体的侧面,上、下面与侧面绝热,那么其温度的控制由圆形区域上的2维反应扩散方程的边界控制模型描述,其控制律也有一些结果[3-4].但物理上还存在如图 1(a)所示的设置圆柱体的温度控制方法,其中的传热介质设为流体.
由于圆柱体上下两面绝热,且仅考虑材料的化学和物理性质是均匀的情况,所以,材料的温度u只依赖x,y和时间t,记为u(x,y,t).根据热传导的数学模型,温度u(x,y,t)满足如下反应扩散方程
设流体的控制系统模型为
其中:状态X (t)∈
${{\mathbb{R}}^{n}}$ 表示流体的温度、密度、压力等物理参数;U(t)∈$\mathbb{R}$ 表示待设计的状态反馈控制输入;矩阵A ∈${{\mathbb{R}}^{n\times n}}$ ,B ∈${{\mathbb{R}}^{n}}$ ,且(A,B)能稳.根据热交换的傅里叶定律,在半径为ε的圆柱界面上的热交换由下面的模型给出
其中CT∈
${{\mathbb{R}}^{n}}$ 和CB ≠0.记
于是根据(1)-(3)式,整个控制系统可以用一个常微分与偏微分方程的级联模型
来表示,其中边界条件(4d)的工程意义是在圆柱体的外侧面设置一开环控制器.子系统(4a)是一常微分方程表示的线性控制系统.如果把(4c)中的CX (t)视为子系统(4b)-(4d)的控制输入,那么这一子系统就是圆环上的反应扩散方程的边界控制系统[5-6].然而,这两个单独的子系统级联而成的控制系统(4a)-(4d)的控制设计及稳定性却与以往已经研究过的级联或者耦合系统不同.其区别在于已经研究过的级联或者耦合系统[7-12]的控制输入是在反应扩散方程的边界上,而级联系统(4a)-(4d)的控制输入是常微分方程表示的线性控制系统(4a)的输入,其能控性的研究都还是空白,也未见关于控制律及稳定性的结果.因此,研究级联系统(4a)-(4d)的控制设计及稳定性具有较强的实际和理论价值.
全文HTML
-
由于圆柱体容器中的物质是均匀的,其中的温度也是对称的,因此,利用极坐标更方便.通过极坐标变换x=rcosθ,y=rsinθ,注意到状态u不依赖于θ,可记为u=u(r,t),于是系统(4)变换为
系统(5b)-(5d)形式上是一维的空间变量.式(5b)中的
$\frac{1}{r}{{u}_{r}}$ 可以用Gauge变换消除[12].然而,这将会导致u的系数依赖r,因此我们倾向于保留这一项.为了设计一个控制来使闭环系统u(x,y,t)达到指数稳定,用Backstepping变换
将系统(5b)-(5d)转换为一个指数稳定的目标系统
其中
$c\ge \frac{1}{4{{\varepsilon }^{2}}}$ ,核函数k待定.后面将会证明目标系统的指数稳定性.通过变换(6),为了满足目标系统的边界条件(7b),u需要满足以下条件
通过方程(5c),还需要满足
将(9)式对t求导,得到
由于u满足方程(5b),利用分部积分,通过子系统(5a),控制输入U(t)需要满足
因为α= CB是一个不为零的常数,所以取控制律为
接下来导出核函数满足的方程.对(6)式关于t进行求导时,因为u满足方程(5b),再通过分部积分和u(R,t)=0,得到
式(6)两边关于r求偏导,可得
其中
将(11),(12)和(13)式带入(7)式,得到
令核函数k(r,s)满足以下条件
于是w满足目标系统(7a).
因为方程(14a)的系数依赖于r和s,要得到核函数方程组(14)的解析解在数学上存在一定困难,~所以本文考虑证明解的存在性.在参考文献[5]中已经给出此类核函数方程解存在性的证明方法.具体步骤如下:首先,利用变换
$\widetilde{k}\left(r\text{, }s \right)=\sqrt{\frac{r}{s}}k\left(r, s \right)$ 消去kr(r,s)和ks(r,s)项;然后,通过变量替换ξ=r-s+R以及ηa=r+s-R可以将偏微分方程转化为一个积分方程;最后,运用迭代法可以证明积分方程解的存在性,从而证明核函数方程组(14)的解的存在性.
-
要得到闭环系统(5b)-(5d)的稳定性,需要证明目标系统(7)的稳定性以及变换(6)的可逆性.由于目标系统(7)不同于以前的任何系统,因此,接下来证明目标系统(7)的稳定性.
令函数f(r,θ)定义在以Γε和ΓR为边界的区域Ω上.如果f不依赖θ,那么它在极坐标下的L2范数‖f‖为
引理1 对于目标系统(7),有
其中‖w(t)‖表示w(r,t)在Ω上的L2范数,即目标系统在L2范数意义下指数稳定.
证 选取李雅普诺夫函数
V(t)对t求导,由于w满足方程(7a),利用边界条件(7b),(7c),可得
通过分部积分,利用边界条件(7b)和(7c),有
通过庞家来不等式以及边界条件(7b)和(7c),有
因此由方程(16),(17),(18)和
$c\ge \frac{1}{4{{\varepsilon }^{2}}}$ ,可以得到利用微分不等式的比较原理,可以得到
因此
即得目标系统(7)在L2范数意义下指数稳定.
变换(6)的可逆性的证明过程与参考文献[5]中证明过程类似.接下来,需要证明如下引理:
引理2 变换(6)和它的逆变换都是有界算子,即存在正整数β和γ使得
证 从变换(6)与范数的性质,可以得到
根据Holder不等式,可以得到
其中
因此
同样地,由逆变换可以得到
其中
此处l(r,s)为逆变换的核函数.
根据引理1和引理2,可以建立闭环系统的稳定性定理.
定理1 设u(r,t)为系统(5b)-(5d)在控制律(10)作用下的闭环信号.于是存在正数σ使得
即闭环系统(5b)-(5d)在L2范数意义下指数稳定.



 下载:
下载: