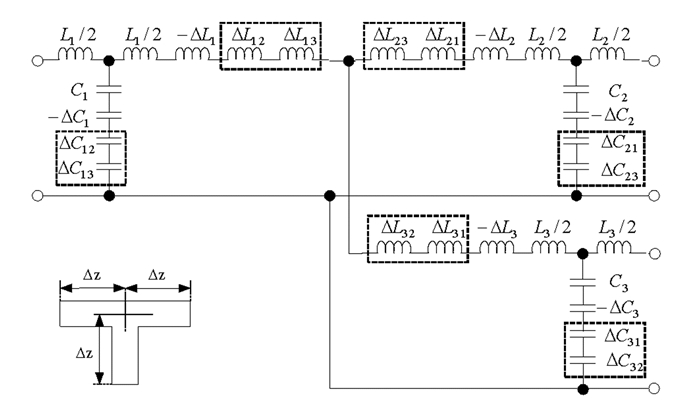
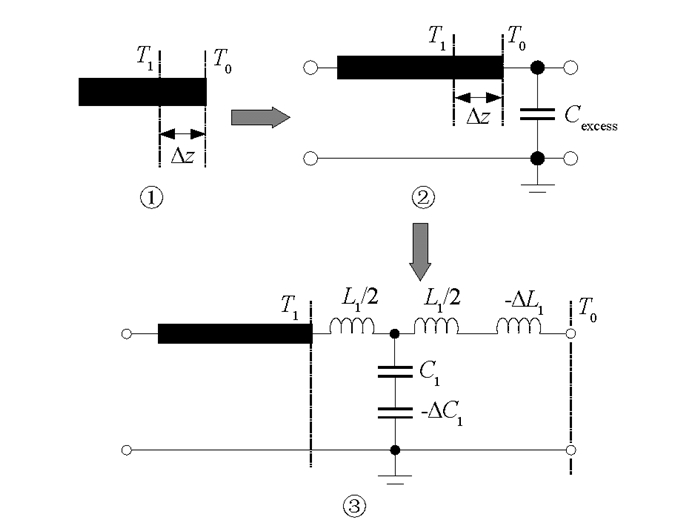
文献[12]基于矩量法的物理解释给出了微带开路线的通用等效电路模型及理论分析，并在此基础上，通过多个开路线的互连，增加各个开路线分支相互作用产生的互电容和互电感，建立了直角拐角、阶梯跳变以及T型接头等复杂结构的不连续性等效电路模型.很显然这种分析方法对于带状线同样适用，本研究将微带开路线的等效电路模型及理论移植到带状线中，建立了带状开路线的LC等效电路模型(图 1)，即将图 1①中带状开路线参考面T₀处的边缘场影响等效为图 1②中的并联电容C_excess，然后依据文献[12]矩量法等效理论得到图 1③中线长为Δz的T₁T₀带状开路线的LC等效电路模型.

从图 1可以看出，带状开路线的不连续性等效电路模型与微带开路线很相似，主要区别在于开路端处边缘场的等效并联电容C_excess计算方法不同，其他LC元器件的计算公式均可以从文献[12]中获得.对于对称带状线来说，其并联电容C_excess可以运用文献[14]中的解析公式进行计算.对于非对称带状线(也就是内导体带偏离中心位置)来说，目前没有文献给出相应的计算公式.一般对于非对称带状开路线来说，由于存在边缘场的影响，它并不是处于理想的开路状态，其实际物理尺寸l₀小于λ/4，两者尺寸差即为边缘场的等效传输线长度Δl，其值为：

式中：λ为介质空间传播的电磁波波长；f₀为理想的λ/4非对称开路线输入阻抗等于0 Ω处的工作频率，可以运用HFSS等仿真软件提取；ε_r为填充介质的介电常数；v₀为自由空间的传播速度(v₀=3×10⁸ m/s).

求解出Δl后，很容易得到非对称带状线的并联电容

式中：β和ω分别为传播常数和角频率，Z₀为非对称带状线的特性阻抗.

很显然，可以将带状线T型接头看作为3个开路线的互连，在此基础上增加各个开路线分支相互耦合作用产生的互电容和互电感，即可获得其等效电路模型(图 2，图中虚线框部分表示产生的互电容和互电感).同理，直角拐角为2个开路线的互连，其等效电路模型只需在图 2基础上删去1个分支及该分支对其他分支产生的互电容和互电感即可得到.

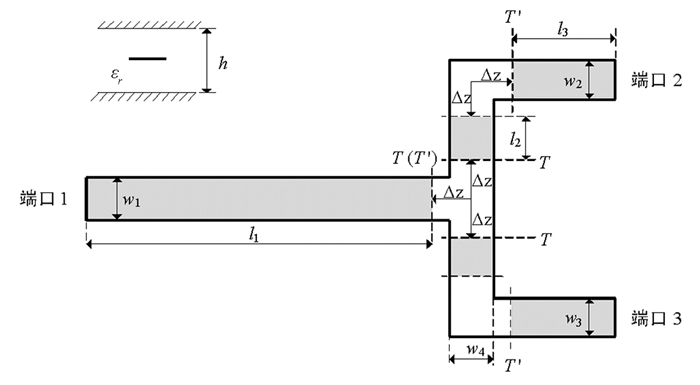
带状线功分器结构见图 3.其中，h为带状线上下接地板之间的距离，w₁，w₂，w₃和w₄分别为带状线功分器的线宽，l₁和l₃分别为端口1至T(T′)处、端口2和3至T′处的距离，l₂为直角拐角与T型接头之间带状传输线线长，Δz为不连续部分的线长.

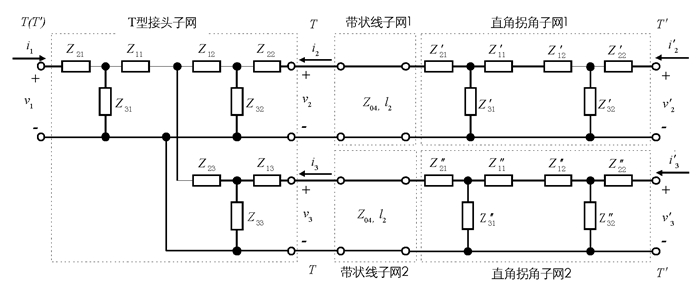
这里假定在准静态条件下进行等效电路模型的构建和分析，且在不连续区域边界外的传输线上仅存在主模传输，不连续部分的线长Δz=h.从图 3中可以看出，整个带状线功分器可以看作为5个带状线(阴影部分)、1个T型接头(中心处)和2个直角拐角(拐角处)的级联.由于直角拐角和T型接头结构存在不连续性，由此会产生一定的传输损耗，因此在分析功分器时应加以考虑.本研究在获得带状开路线的不连续性等效电路模型基础上，分别将T型接头和直角拐角看作3个和2个开路线的级联，建立了带状线功分器参考面T′区域的等效电路模型(图 4)，然后只需将参考面由T′处分别外延至3个端口处，就可以实现对整个带状线功分器的等效电路分析.

从图 4中看出，参考面T′区域的等效电路模型可以划分为T型接头子网、带状线子网1、带状线子网2、直角拐角子网1和直角拐角子网2，各个子网中等效阻抗的计算可以从文献[12]中获得.

T型接头子网的各阻抗为：

直角拐角子网1的各阻抗为：

直角拐角子网2中各阻抗表达式与直角拐角子网1类似，这里不再给出. (3)-(17)式中相关参数可以运用文献[12]中的公式进行计算.带状线子网1和带状线子网2可以根据传输线理论进行分析^[15].

接下来，主要推导图 4中参考面T′区域的等效电路模型对应的散射参数计算公式，以便最终计算出整个带状线功分器的散射参数.

ABCD传输矩阵参量特别适合描述级联网络的特性，由其定义可知整个级联网络的ABCD传输矩阵等于各个子网络的ABCD传输矩阵的乘积^[15]，因此很容易得到图 4中带状线子网1与直角拐角子网1级联后的ABCD传输矩阵，记为$\left[{\begin{array}{*{20}{c}} {{A_2}}&{{B_2}}\\ {{C_2}}&{{D_2}} \end{array}} \right]$.

式中：β表示带状线的传播常数，Z₀₄表示带状线子网带状线的特性阻抗.同理，也可以得到带状线子网2与直角拐角子网2级联后的ABCD传输矩阵，记为$\left[{\begin{array}{*{20}{c}} {{A_3}}&{{B_3}}\\ {{C_3}}&{{D_3}} \end{array}} \right]$.

同样由传输矩阵的定义可知，两个ABCD传输矩阵与输入输出端口处电压、电流的关系为：

参考面T处的T型接头子网阻抗矩阵[z_ij](i=1，2，3；j=1，2，3)可以由文献[15]计算获得，且与其3个分支端口处的电压、电流存在关系：

将方程组(19)和(20)中i₂，i₃代入方程组(21)中，经过移项、合并操作后可得：

为了简化表达式，假定X₁=A₂+z₂₂C₂，X₂=z₂₃C₃，X₃=B₂+z₂₂D₂，X₄=z₂₃D₃；Y₁=z₃₂C₂，Y₂=A₃+z₃₃C₃，Y₃=z₃₂D₂，Y₄=B₃+z₃₃D₃，将它们代入方程组(22)中第2和第3方程后，联立求解可得：

参考面T′处的阻抗矩阵[z′_ij](i=1，2，3；j=1，2，3)与其3个分支端口处的电压、电流存在如下关系：

对照式(23)、式(24)与方程组(25)中第2和第3方程，可以得到阻抗矩阵[z′_ij]中的第2和第3行的元素值.然后将方程组(25)中第2和第3方程代入方程组(22)中第1个方程得到阻抗矩阵[z′_ij]中第1行的元素值.

此时已由参考面T处阻抗矩阵[z_ij]推导出了参考面T′处的阻抗矩阵[z′_ij]，成功实现了将参考面由T移至T′处.然后根据阻抗矩阵与散射矩阵之间的关系^[16]，将阻抗矩阵[z′_ij]转换为散射矩阵[S]，也就是此时得到了参考面T′处的散射矩阵.

从图 3可知，需要将带状线功分器从参考面T′分别外延至3个端口(外延传输线长度分别为l₁，l₃和l₃)，才能得到整个带状线功分器的散射参数.由传输线基本理论可知，带状线功分器的散射矩阵[S′]与参考面T′处的散射矩阵[S]之间的关系，为

其中：

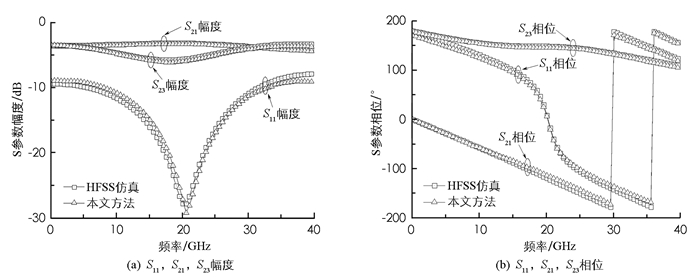
为了验证本研究所提出的等效电路模型及理论的正确性，设计了一个带状线功分器，其结构示意图见图 1.基本参数：ε_r＝12.9，h=40 μm，w₁=w₂=w₃=w₄=7.8 μm，l₁=1 100 μm，l₂=24 μm，l₃=80 μm，不连续性线长Δz=40 μm. 图 5给出了运用本研究提出的等效电路分析法和三维电磁仿真软件HFSS两种方法计算所得散射参数的对比曲线.

从图 5中可以发现，运用本研究提出的等效电路分析法和HFSS软件仿真两种方法计算所得该功分器的散射参数S₁₁，S₂₁，S₂₃幅度和相位基本吻合，其最大误差小于5%，且平均误差小于2%，这充分验证了本研究所提出的等效电路模型的正确性，也说明本研究方法考虑了带状线功分器结构中直角拐角和T型接头不连续性部分所引入的传输损耗，有效地克服了传统分析方法的不足.同时也可以发现：图 5(a)中本研究方法计算出的S₁₁幅度结果较HFSS软件仿真结果向高频方向发生一定的偏移，且当f>35 GHz时，误差随着频率上升逐渐增大；图 5(b)中S₁₁相位在f < 15 GHz和f>27 GHz、S₂₁相位在f>18 GHz的频率范围内产生了一定的误差，但2%的平均误差对于工程设计和分析来说是完全可以接受的.产生上述偏移和误差的原因主要在于本研究所基于的微带开路线等效电路模型及计算公式的不够精确引起的，同时本研究提出的等效电路模型是在准静态条件下进行构建和分析的，因此随着工作频率的上升，一旦超过准静态频率界限时相关参数的计算误差也会随之增大.后期可以通过空间映射等优化算法^[17-18]来进一步优化等效电路模型，通过使用Q3D等专用工具软件提取等效电路模型中的分布电容、分布电感和特性阻抗来降低计算误差，从而保证更加准确地分析此类微波集成电路组件.

本研究在已有的微带开路线不连续性等效电路模型及理论基础上，提出了一种带状线功分器的等效电路分析方法，结合算例验证和分析，本研究方法的计算结果与HFSS软件仿真结果吻合良好，该功分器散射参数的平均误差小于2%，较为准确地分析了带状线功分器，也为设计和分析微波集成电路系统中此类无源器件提供了参考.