设X=C([－τ，0]，$\mathbb{R}_ + ^4$)是[－τ，0]到$\mathbb{R}_ + ^4$上的连续映射全体构成的Banach空间，且定义范数‖φ‖= $\mathop {\max }\limits_{ - \tau \le \theta \le 0} $ －τ≤θ≤0 |φ(θ)|，φ∈X. 系统(1)的初值条件如下：

其中：φ=(φ₁(θ)，φ₂(θ)，φ₃(θ)，φ₄(θ))∈X，φ_i(θ)≥0，φ_i(0)>0，i=1，2，3，4. 根据泛函微分方程的基本理论，可知系统(1)满足初值条件(2)有唯一解.

定理1  设(x(t)，y(t)，v(t)，z(t))是系统(1)的满足初始条件(2)的唯一解，则对任意t>0，解是正的且有界的.

证  首先，证明y(t)是正的. 假设结论不成立，即存在t>0，使得y(t)=0. 令t₁=inf{t：t>0，y(t)=0}，因为y(0)>0，故y′(t₁)≤0. 根据系统(1)的第三个方程，有y′(t₁)=(1－u₁)βx(t₁)v(t₁). 下面证明y′(t₁)>0. 由系统(1)的第一个和第三个方程有：

可知x(t₁)>0，v(t₁)>0，故y′(t₁)>0，矛盾. 故y(t)为正. 易得x(t)，v(t)均为正. 下证z(t)为正. 假设结论不成立，即存在t>0，使得z(t)=0. 令t₂=inf{t：t>0，z(t)=0}，则z′(t₂)≤0，z(t₂)=0. 由τ>0，t₂－τ < t₂，得z(t₂－τ)>0，又因y(t₂－τ)>0，可得z′(t₂)=sy(t₂－τ)z(t₂－τ)>0，矛盾. 故z(t)为正.

下证系统(1)解的有界性. 令

沿着系统(1)对t求导

其中$\tilde n = \min \left\{ {\frac{\sigma }{2}, \mu , k} \right\}$. 由比较定理可得

其中ε是任意小的正常数. 故系统(1)的解是有界的.

利用下一代矩阵法^[14]，可得系统(1)的基本再生数和免疫再生数：

下面我们考虑平衡点的存在性，令系统(1)右边4个方程为0，可得：

显然，系统(1)存在无病平衡点E₀=(x₀，0，0，0)= $\left( {\frac{\mathit{\Lambda }}{\sigma }, 0, 0, 0} \right)$. 当R₀>1时，存在无免疫平衡点E₁=(x₁，y₁，v₁，0)，其中

当R₁>1时，存在地方病平衡点E₂=(x₂，y₂，v₂，z₂)，其中

为了简化免疫再生数R₁，定义R₁^*= $\frac{{\left( {1 - {u_1}} \right)\left( {1 - {u_2}} \right)\beta ms\mathit{\Lambda }}}{{\sigma \mu s(p + \sigma ) + \left( {1 - {u_1}} \right)\left( {1 - {u_2}} \right)\beta m\sigma k}}$，有如下引理成立：

引理1  (a) R₁ < 1⇔R₁^* < 1；

(b) R₁>1⇔R₁^*>1；

(c) R₁=1⇔R₁^*=1.

证  先证明(a)成立：

类似地，(b)和(c)也成立.

定理2  当R₀ < 1时，无病平衡点E₀局部渐近稳定；当R₀>1时，E₀不稳定.

证  系统(1)线性化后在E₀处的特征方程为

显然方程(3)有两个负特征根λ=－σ，λ=－k. 其它特征根λ满足方程

显然μ+p+σ>0，当R₀ < 1时，

故方程(4)的两个特征根实部均为负. 因此，当R₀ < 1时，无病平衡点E₀局部渐近稳定. 当R₀>1时，方程(4)的两个特征根实部一正一负，故E₀不稳定.

定理3  当R₀≤1时，无病平衡点E₀全局渐近稳定.

证  定义Lyapunov泛函如下：

沿着系统(1)轨线的全导数为：

当R₀≤1时，V′₁≤0. V′₁=0当且仅当(x，y，v，z)=E₀. 因此，{E₀}是{(x，y，v，z)|V′₁(t)=0}的最大不变集. 根据LaSalle不变集原理，可知E₀全局渐近稳定.

定理4  当R₁ < 1 < R₀时，无免疫平衡点E₁局部渐近稳定；当R₁>1时，E₁不稳定.

证  系统(1)线性化后在E₁处的特征方程为

其中

对于方程

当R₀>1时，y₁>0，故K₁，K₂，K₃均大于0.

由Hurwitz判据法可知方程(6)的特征根均有负实部. 下面考虑方程λ+k－sy₁e^－λτ=0.

1) 当τ=0时，λ=sy₁－k. 定义函数

f(x)对于x求导，有

当R₀>1时，(1－u₁)(1－u₂)βmΛ>μσ(p+σ)>σμp，故对所有的x>0有f′(x) < 0，函数f(x)单调递减. 当${R_1} = \frac{{\left( {1 - {u_1}} \right)\left( {1 - {u_2}} \right)\beta m}}{{\mu (p + \sigma )}}{x_2} = \frac{{{x_2}}}{{{x_1}}} < 1$，有x₂ < x₁. 结合f(x)单调递减，可知y₁=f(x₁) < f(x₂)=y₂，则λ=sy₁－k < sy₂－k=0. 因此当τ=0时，若R₁ < 1 < R₀，无免疫平衡点E₁局部渐近稳定.

2) 当τ>0时，假设方程λ+k－sy₁e^－λτ=0有纯虚根λ=±iω(ω>0). 代入并分离实部和虚部有

等式两边分别平方再求和有

由1)可知，当R₁ < 1 < R₀时，sy₁－k < 0，这与(7)式矛盾. 故方程λ+k－sy₁e^－λτ=0的特征值有负实部. 因此，当τ>0时，若R₁ < 1 < R₀，方程(5)的特征根均有负实部，故无免疫平衡点E₁局部渐近稳定.

当R₁>1时，R₁= x₂ x₁ >1，即x₂>x₁，故y₂ < y₁. 设P(λ)=λ+k－sy₁e^－λτ，P(0)=k－sy₁ < k－sy₂=0，$\mathop {\lim }\limits_{\lambda \to + \infty } P(\lambda ) > 0$. 可知方程P(λ)=0的特征根有正实部，此时E₁不稳定.

定理5  当R_H < 1 < R₀ < 1+ $\frac{\sigma }{p}$时，无免疫平衡点E₁全局渐近稳定.

证  定义Lyapunov泛函如下：

沿着系统(1) 轨线的全导数为：

其中

可知R_H < 1 < R₀ < 1+ $\frac{\sigma }{p}$时V′₂≤0. V′₂=0当且仅当(x，y，v，z)=E₁. 因此，E₁是{(x，y，v，z)| V′₂(t)=0}的最大不变集. 根据LaSalle不变集原理，E₁全局渐近稳定.

系统(1)线性化后在E₂处的特征方程为

其中

当τ=0时，(8)式变为

其中

当R₁>1时，a_i>0，i=1，2，3，4.

根据Routh-Hurwitz判据知当a₁a₂a₃－a₃²－a₁²a₄>0时，方程(9)的特征根均有负实部. 根据以上分析，有如下结论：

定理6  当τ=0，R₁>1时，若a₁a₂a₃－a₃²－a₁²a₄>0，系统(1)的地方病平衡点E₂局部渐近稳定.

现在我们考虑当τ>0时，纯虚根的存在性. 假设方程(8)有纯虚根iω(ω>0)，代入到方程(8)中有

分离实部和虚部有

两边分别平方再求和，可得

其中

定义函数

因此，如果方程(8)有纯虚根iω(ω>0)，那么方程

有正实根ω².

假设方程(10)有m(1≤m≤4)个正实根，分别表示为x_n(1≤n≤m)，我们有

解出

其中：1≤n≤m，j=0，1，2，…. 设方程(8)的特征根是λ(τ)=α(τ)+iω(τ)，满足α(τ_n^(j))=0，ω(τ_n^(j))=ω.

为了讨论系统(1)的Hopf分支存在性问题，有如下定理：

定理7  ${\left. {\frac{{{\rm{d}}\alpha _n^{(j)}}}{{{\rm{d}}\tau }}} \right|_{\tau = \tau _n^{(j)}}}{\rm{与}}{\left. {\frac{{{\rm{d}}F}}{{{\rm{d}}\tau }}} \right|_{x = {x_n}}}$有相同的符号.

证  方程(8)两边对τ求导，可得

因此有

显然${\left. {{{\left. {\frac{{{\rm{d}}\alpha _n^{(j)}}}{{{\rm{d}}\tau }}} \right|}_{\tau = \tau _n^{(j)}}}与\frac{{{\rm{d}}F}}{{{\rm{d}}\tau }}} \right|_{x = {x_n}}}$有相同的符号.

由Hopf分支理论，我们有如下定理：

定理8  1) 当(10)式无正实根时，对任意的τ≥0，地方病平衡点E₂局部渐近稳定；

2) 当(10)式有正实根时，对于τ∈[0，τ₀)，地方病平衡点E₂局部渐近稳定，其中τ₀=min{τ_n^(j)|1≤n≤m，j=0，1，2，…}；

3) 当(10)式有正实根时，系统(1)在τ=τ₀处产生Hopf分支.

证  1) 结论显然成立.

2) 根据τ₀的定义可知，当τ∈[0，τ₀)时，(10)式没有正实根，即特征根没有穿过虚轴. 所以对所有的τ∈[0，τ₀)，(8) 式的特征根都具有负实部，此时E₂局部渐近稳定.

3) 因为x₀是方程(10) 的单根，可知F′(x₀)≠0. 由定理7可知${\left. {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}\tau }}} \right|_{\tau = {\tau _0}}} \ne 0$. 假设${\left. {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}\tau }}} \right|_{\tau = {\tau _0}}} < 0$，当τ=τ₀－ε(ε为任意小的正数)时，方程(8)的特征根有正实部，这与2)是矛盾的. 故${\left. {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}\tau }}} \right|_{\tau = {\tau _0}}} > 0$，且当τ=τ₀时，方程(8)的特征根实部为0或负. 这意味着系统(1)产生Hopf分支.

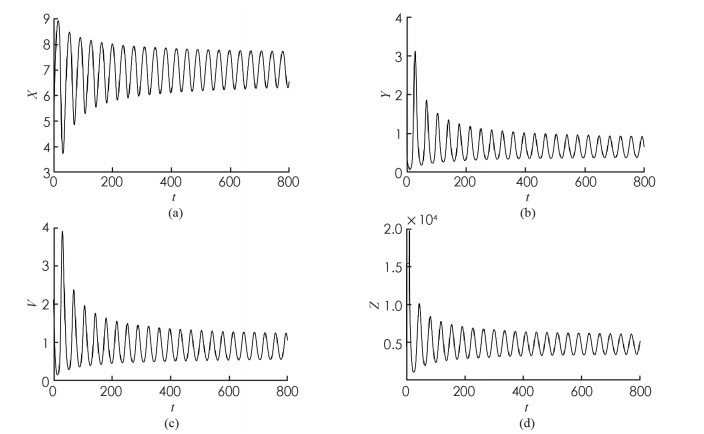
为了验证本文的理论结果，取文献[13，15-16]中的数据：Λ=10；β=4.430 1；p=0.12；σ=1.056 1；q=0.000 7；m=5.352 5；μ=0.381 8；s=9.212 9；k=5.375 2. 令u₁=u₂=0.9. 可计算出R₁=3.748 9，地方病平衡点E₂存在且局部渐近稳定，E₂=(7.099 3，0.583 4，0.817 9，461.86)，τ₀=9.704 3.

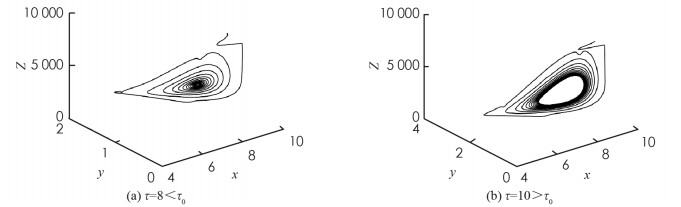
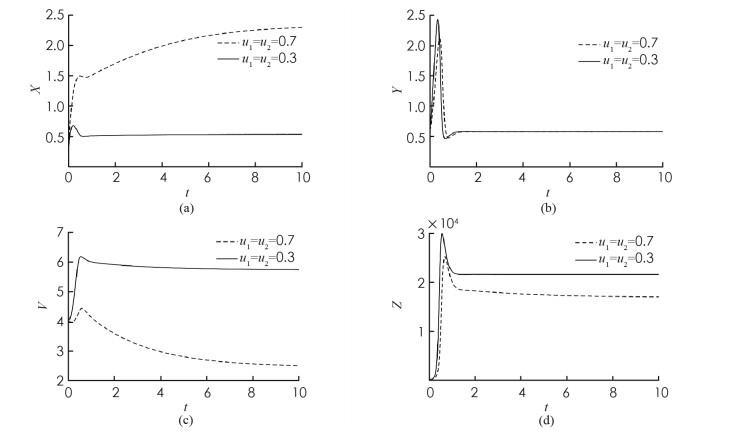
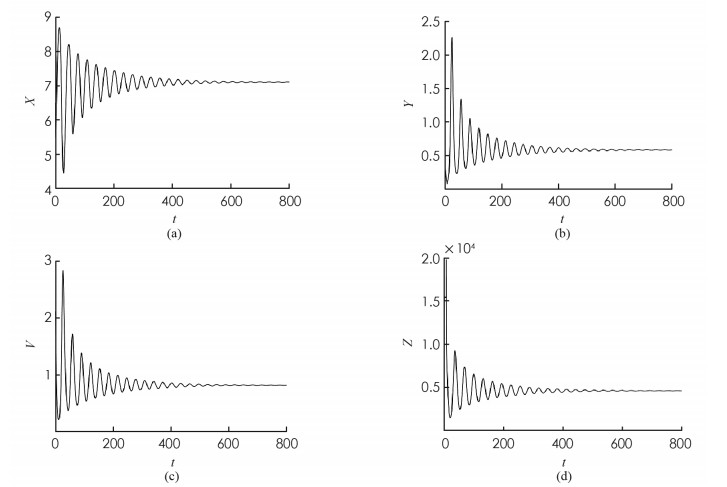
首先，考虑解的长期行为. 当τ=8 < τ₀时，地方病平衡点局部渐近稳定(图 1)；当τ=10>τ₀时，地方病平衡点不稳定并出现了周期解(图 2)；图 3展示τ=8和τ=10时的相图. 数值结果与理论结果相一致. 其次，为了探究药物治疗策略对于控制病毒传播的影响，分别取u₁=u₂=0.7和u₁=u₂=0.3. 图 4中(a)表明治疗效率越高，未感染细胞浓度的平衡态会明显增加；(b)表明对于不同的治疗效率，虽然感染细胞浓度最终平衡态相同，但是药物治疗效率越高，感染细胞浓度的峰值会有效下降；(c)表明治疗效率越高，自由病毒粒子浓度明显降低；(d)表示治疗效率对降低CTL免疫细胞浓度的影响.

本文研究了一个具有药物治疗和CTL免疫时滞的HBV模型，其中药物治疗包括抑制病毒感染和减少自由病毒粒子释放，免疫包括细胞溶解免疫和非细胞溶解免疫. 计算两个阈值：基本再生数R₀和免疫再生数R₁. 应用LaSalle不变集原理和构造Lyapunov泛函得到3个平衡点的稳定性. 当R₀ < 1时，无病平衡点全局渐近稳定；当R_H < 1 < R₀ < 1+ $\frac{\sigma }{p}$时，无免疫平衡点全局渐近稳定. 通过理论分析和数值模拟结果可以看出药物治疗的效率对减少感染细胞(y)和自由病毒粒子(v)浓度有显著效果. 其次，时滞的大小影响地方病平衡点的稳定性：当τ∈[0，τ₀)时，地方病平衡点局部渐近稳定；当τ>τ₀时，地方病平衡点不稳定. 当τ=τ₀时，系统产生Hopf分支. 定理5的R_H < 1 < R₀ < 1+ $\frac{\sigma }{p}$作为E₁全局稳定成立的条件，或许可以被削弱；另外，本文未得出地方病平衡点E₂稳定性的具体结论，今后可进一步讨论.