高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

异构平台上基于OpenCL的矩阵乘并行算法

,  ,  , 

上一篇

下一篇

肖汉, 肖诗洋, 李彩林, 等. 异构平台上基于OpenCL的矩阵乘并行算法[J]. 西南大学学报（自然科学版）, 2020, 42(11): 147-153. doi: 10.13718/j.cnki.xdzk.2020.11.017
引用本文: 肖汉, 肖诗洋, 李彩林, 等. 异构平台上基于OpenCL的矩阵乘并行算法[J]. 西南大学学报（自然科学版）, 2020, 42(11): 147-153. doi: 10.13718/j.cnki.xdzk.2020.11.017
shu
XIAO Han, XIAO Shi-yang, LI Cai-lin, et al. AMatrix Multiplication Parallel Algorithm Based on OpenCL on Heterogeneous Platforms[J]. Journal of Southwest University Natural Science Edition, 2020, 42(11): 147-153. doi: 10.13718/j.cnki.xdzk.2020.11.017
Citation: XIAO Han, XIAO Shi-yang, LI Cai-lin, et al. AMatrix Multiplication Parallel Algorithm Based on OpenCL on Heterogeneous Platforms[J]. Journal of Southwest University Natural Science Edition, 2020, 42(11): 147-153. doi: 10.13718/j.cnki.xdzk.2020.11.017
shu

异构平台上基于OpenCL的矩阵乘并行算法

  • 1.

    郑州师范学院 信息科学与技术学院，郑州 450044

  • 2.

    东北林业大学 土木工程学院，哈尔滨 150040

  • 3.

    山东理工大学 建筑工程学院，山东 淄博 255000

  • 4.

    郑州大学 信息工程学院，郑州 450001

  • 基金项目: 国家自然科学基金项目(41601496，41701525，61572444)；山东省自然科学基金项目(ZR2017LD002)；山东省重点研发计划项目(2018GGX106002)
详细信息
    作者简介:

    肖汉(1970-)，男，教授，博士后，主要从事大规模并行算法研究与设计、遥感大数据并行处理的研究 .

    通讯作者: 李彩林，博士，硕士研究生导师; 

  • 中图分类号: TP311

AMatrix Multiplication Parallel Algorithm Based on OpenCL on Heterogeneous Platforms

  • 1.

    School of Information Science and Technology, Zhengzhou Normal University, Zhengzhou 450044, China

  • 2.

    School of Civil Engineering, Northeast Forestry University, Harbin 150040, China

  • 3.

    School of Civil and Architectural Engineering, Shandong University of Technology, Zibo, Shandong 255000, China

  • 4.

    School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China

  • 摘要: 在分析开放式计算语言(OpenCL)平台底层硬件构架的基础上，从数据本地化、计算资源利用率和访存带宽利用率等多个不同角度优化了矩阵乘算法，并实现了矩阵乘算法在OpenCL架构下的加速.实验数据显示，与基于CPU的单线程算法、基于OpenMP多线程算法和基于统一计算设备架构(CUDA)并行算法相比，基于OpenCL架构的矩阵乘并行算法效率更高.
    Abstract: Based on an analysis of the underlying hardware architecture of Open Computing Language (OpenCL) platform, this paper optimizes the matrix multiplication algorithm from several different angles, such as the data localization, the computing resource utilization ratio and the utilization ratio of the memory bandwidth, and realizes the acceleration of matrix multiplication algorithm in OpenCL architecture. The experimental data show that the matrix multiplication parallel algorithm based on OpenCL architecture is more efficient than the single thread algorithm based on CPU, the multi-thread algorithm based on Open Multi-Processing (OpenMP) and theparallel algorithm based on Compute Unified Device Architecture (CUDA).
  • 加载中

  • 图 1  矩阵乘并行算法执行模式

    下载: 全尺寸图片 幻灯片

    图 2  不同计算平台下矩阵乘并行算法的加速比对比

    下载: 全尺寸图片 幻灯片
    算法  OpenCL架构上的矩阵乘法算法
       输入：矩阵An×n，Bn×n.
       输出：矩阵Cn×n.
       Begin
         for all Sx×Sy par-do
            for i=0 to Sx-1 do
              for j=0 to Sy-1 do
                Ci，j=0
                for k=0 to Sx-1 do
                  Ci，j=Ci，j+Ai， k*Bk，j
               end for
             end for
           end for
         end for
       End
    下载: 导出CSV

    表 1  工作组大小对运算速度的影响

    工作组中的工作项数 运行时间/ms
    64 7.726
    96 5.621
    128 5.484
    160 4.213
    192 3.182
    224 3.282
    256 3.434
    下载: 导出CSV

    表 2  不同计算平台下矩阵乘算法执行时间

    矩阵大小 串行处理时间/s 并行处理时间/s
    OpenMP CUDA AMD OpenCL NVIDIA OpenCL
    100×100 0.006 0.003 0.002 0.002 0.002
    200×200 0.057 0.018 0.010 0.013 0.010
    400×400 0.461 0.088 0.066 0.080 0.055
    600×600 3.182 0.583 0.228 0.228 0.203
    800×800 8.789 1.598 0.517 0.459 0.429
    1 000×1 000 20.362 3.695 1.031 1.012 0.898
    1 400×1 400 57.796 10.321 2.793 2.599 2.353
    下载: 导出CSV

    表 3  不同计算平台下矩阵乘并行算法性能对比

    序号 矩阵大小 加速比 相对加速比1 相对加速比2
    OpenMP CUDA AMD OpenCL NVIDIA OpenCL
    1 100×100 2.00 3.00 3.00 3.00 1.50 1.00
    2 200×200 3.17 5.70 4.38 5.70 1.80 1.00
    3 400×400 5.24 6.99 5.76 8.38 1.60 1.20
    4 600×600 5.46 13.96 13.96 15.67 2.87 1.12
    5 800×800 5.50 17.00 19.15 20.49 3.73 1.21
    6 1 000×1 000 5.51 19.75 20.12 22.67 4.11 1.15
    7 1 400×1 400 5.60 20.69 22.24 24.56 4.39 1.19
    下载: 导出CSV
  • [1] HOSSEINI RAD M, PATOOGHY A, FAZELI M. An Efficient Programming Skeleton for Clusters of Multi-Core Processors [J]. International Journal of Parallel Programming, 2018, 46(6): 1094-1109. doi: 10.1007/s10766-017-0517-y
    [2] FIALKO S. Parallel Direct Solver for Solving Systems of Linear Equations Resulting from Finite Element Method on Multi-Core Desktops and Workstations [J]. Computers & Mathematics with Applications, 2015, 70(12): 2968-2987.
    [3] CABRERA W, ORDONEZ C. Scalable Parallel Graph Algorithms with Matrix-Vector Multiplication Evaluated with Queries [J]. Distributed and Parallel Databases, 2017, 35(3-4): 335-362. doi: 10.1007/s10619-017-7200-6
    [4] PARK S M, CHANG K Y, HONG D, et al. Subquadratic Space Complexity Multiplier Using Even Type GNB Based on Efficient Toeplitz Matrix-Vector Product [J]. IEEE Transactions on Computers, 2018, 67(12): 1794-1805. doi: 10.1109/TC.2018.2836425
    [5] LIMA F A, MORENO E D, DIAS W R A. Performance Analysis of a Low Cost Cluster with Parallel Applications and ARM Processors [J]. IEEE Latin America Transactions, 2016, 14(11): 4591-4596. doi: 10.1109/TLA.2016.7795834
    [6] ACER S, TORUN T, AYKANAT C. Improving Medium-Grain Partitioning for Scalable Sparse Tensor Decomposition [J]. IEEE Transactions on Parallel and Distributed Systems, 2018, 29(12): 2814-2825. doi: 10.1109/TPDS.2018.2841843
    [7] LIANG Y, TANG W T, ZHAO R Z, et al. Scale-Free Sparse Matrix-Vector Multiplication on Many-Core Architectures [J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2017, 36(12): 2106-2119. doi: 10.1109/TCAD.2017.2681072
    [8] KRUCHININA A, RUDBERG E, RUBENSSON E H. Parameterless Stopping Criteria for Recursive Density Matrix Expansions [J]. Journal of Chemical Theory and Computation, 2016, 12(12): 5788-5802. doi: 10.1021/acs.jctc.6b00626
    [9] ZHENG D, MHEMBERE D, LYZINSKI V, et al. Semi-External Memory Sparse Matrix Multiplication for Billion-Node Graphs [J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(5): 1470-1483. doi: 10.1109/TPDS.2016.2618791
    [10] 崔翔, 李晓雯, 陈一峯.基于Parray数组类型的矩阵乘法实现[J].计算机学报, 2014, 37(12): 2564-2573.
    [11] 周磊涛, 陶耀东, 刘生, 等.基于FPGA的Systolic乘法技术研究[J].计算机工程与科学, 2015, 37(9): 1632-1636.
    [12] 刘沛华, 鲁华祥, 龚国良, 等.基于FPGA的全流水双精度浮点矩阵乘法器设计[J].智能系统学报, 2012, 7(4): 302-306.
    [13] 朱敏, 唐波, 赵娟, 等.布尔矩阵乘的分布式异构并行优化[J].计算机工程与科学, 2017, 39(4): 634-640.
    [14] LASTOVETSKY A, REDDY MANUMACHU R. New Model-Based Methods and Algorithms for Performance and Energy Optimization of Data Parallel Applications on Homogeneous Multicore Clusters [J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(4): 1119-1133. doi: 10.1109/TPDS.2016.2608824
    [15] 王云龙, 吴瑛.基于GPU的相关干涉仪算法实现[J].信息工程大学学报, 2015, 16(1): 41-45.
    [16] 张梦元.基于CUDA的矩阵乘法的并行实现[J].信息通信, 2012(2): 20-21.
    [17] BERI T, BANSAL S, KUMAR S. The Unicorn Runtime: Efficient Distributed Shared Memory Programming for Hybrid CPU-GPU Clusters [J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(5): 1518-1534. doi: 10.1109/TPDS.2016.2616314
    [18] 龙卓群, 王晓瑜, 王昌明.基于DCT预测编码的Epiphany-OpenCL大矩阵乘并行计算[J].自动化与仪表, 2017, 32(7): 16-21.
    [19] 刘鹏, 王学奎, 黄宜华, 等.基于Spark的极限学习机算法并行化研究[J].计算机科学, 2017, 44(12): 33-37.
    [20] GU R, TANG Y, TIAN C, et al. Improving Execution Concurrency of Large-Scale Matrix Multiplication on Distributed Data-Parallel Platforms [J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(9): 2539-2552. doi: 10.1109/TPDS.2017.2686384
  • 加载中
图( 2) 表( 4)
计量
  • 文章访问数:  939
  • HTML全文浏览数:  939
  • PDF下载数:  277
  • 施引文献:  0
出版历程
  • 收稿日期:  2018-12-07
  • 刊出日期:  2020-12-20

异构平台上基于OpenCL的矩阵乘并行算法

    通讯作者: 李彩林，博士，硕士研究生导师; 
    作者简介: 肖汉(1970-)，男，教授，博士后，主要从事大规模并行算法研究与设计、遥感大数据并行处理的研究
  • 1. 郑州师范学院 信息科学与技术学院，郑州 450044
  • 2. 东北林业大学 土木工程学院，哈尔滨 150040
  • 3. 山东理工大学 建筑工程学院，山东 淄博 255000
  • 4. 郑州大学 信息工程学院，郑州 450001
  • 收稿日期:  2018-12-07
基金项目:  国家自然科学基金项目(41601496，41701525，61572444)；山东省自然科学基金项目(ZR2017LD002)；山东省重点研发计划项目(2018GGX106002)

摘要: 在分析开放式计算语言(OpenCL)平台底层硬件构架的基础上，从数据本地化、计算资源利用率和访存带宽利用率等多个不同角度优化了矩阵乘算法，并实现了矩阵乘算法在OpenCL架构下的加速.实验数据显示，与基于CPU的单线程算法、基于OpenMP多线程算法和基于统一计算设备架构(CUDA)并行算法相比，基于OpenCL架构的矩阵乘并行算法效率更高.

English Abstract

    全文HTML

  • 矩阵乘法是科学计算中最基本的操作之一[1-2].然而，由于矩阵乘法运算数据量大、计算密集度高，许多传统数据处理方法都难以满足实时性要求.如何进行大数据量的快速处理，降低运算时间，提高整体应用系统的时效性已显得尤为重要[3].

    近年来，随着并行算法技术与并行处理构架的发展，多核CPU，FPGA，GPU等新型加速平台开始被研究和运用[4-7].开放式计算语言(open computing language，OpenCL)是一种通用的国际标准，可用来在不同架构CPU，GPU，FPGA等设备上使用统一的接口来设计，包括编程语言规则、程序设计语言、函数库、应用编程接口等[8].

    目前，国内外研究学者在矩阵乘算法的加速和优化方面已有一些代表性工作[9-20]，但是算法本身加速效果均不明显.本文将根据矩阵乘算法的运算特性和GPU架构特征，实现OpenCL加速的矩阵乘并行算法.同时，通过性能参数传递机制，实现了该算法在不同计算平台上的性能移植.

1.   并行化实现与优化矩阵乘算法

    1.1.   并行算法描述

  • 一个n×n的方阵A乘以n×n的方阵B可得一个n×n的方阵C：

    其中C矩阵的元素$ {c_{ij}} = \sum\limits_{k = 0}^{n - 1} {{a_{ik}}{b_{kj}}} $，0≤i，j≤n-1.在基于GPU实现的矩阵乘法中，将n阶矩阵分成Sx×Sy个大小为m×r的矩阵子块，其中：m=n/Sx，r=n/Sy，Sx与Sy分别为GPU在x，y方向设置的工作组大小.使用Sx×Sy个工作组执行分块乘时，每个工作组计算一个Ci，j块.

    • 1.2.   并行算法执行模式

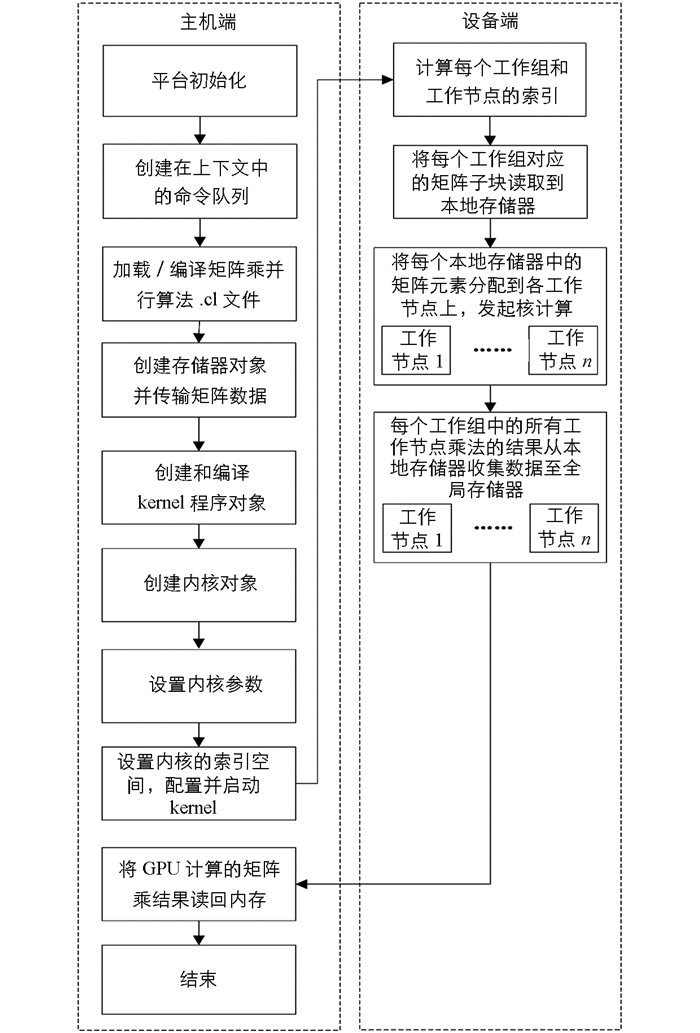
  • 基于OpenCL的矩阵乘GPU并行化处理执行模式见图 1.

    • 1.3.   矩阵乘并行算法在OpenCL上的实现

    1.3.1.   并行算法设计

  • 在GPU上创建矩阵乘并行计算工作项网格.计算网格的输入数据是方阵A和方阵B，包括Sx×Sy个工作组，每个工作组处理一个矩阵子块.每个工作组包括32*32个工作项，每个工作项处理矩阵子块中的一个矩阵元素.

    计算网格的输入矩阵数据一般都存储在慢速全局存储器中，在计算矩阵乘结果每个矩阵元素时，需要频繁地从全局存储器读取计算数据.设输入n维矩阵方阵，则生成n维结果矩阵方阵进行乘—加运算的时间复杂度为O(n3)，所需要的全局存储器访问的次数为n3量级.也就是说，每计算一个结果矩阵元素就需要进行n次全局存储器的访问，这将严重影响算法的效率.本地存储器相对于全局存储器具有更高的访存速度，为了缓解显存带宽与运算性能之间的不平衡，可先将矩阵子块数据从全局存储器中取出，存储到高速本地存储器中，供一个工作组内所有的工作项使用，每次计算只需要从本地存储器中读取数据即可.但由于可供每个工作项使用的本地存储器仅为16 KB，当矩阵子块中数据量较多时，无法一次性放入本地存储器.这就需要适当控制矩阵子块的大小，保证每个矩阵子块的数据放入本地存储器.最后将结果矩阵数据转储在GPU的全局存储器中.

    • 1.3.2.   计算核心的启动配置

  • N维索引空间NDRange与工作组的大小会影响到加速的性能.矩阵乘并行算法的计算网格配置时二维工作空间NDRange的维度应取得较大.这样，就有更多的工作组可以被分配到GPU的CU中. CU以warp为单位执行工作组，在同一个CU上可以同时存在多个工作组的上下文和多个warp上下文，但一个时刻只有一个warp被执行.如果有多个warp能被调度，GPU的容许时延机制会按照优先级进行调度，这样利用零开销的工作项或warp调度选取其他工作项或warp执行，便能充分利用硬件资源来掩盖延迟时间.如果CU只分配了一个工作组，由于属于同一个工作组的若干个warp会有比较大的几率会同时进入长延时操作，就会使CU中的PE处于长时间等待.而属于不同工作组的warp在同一个CU上执行时，当一个工作组的所有warp都进入长延时操作，在其他工作组中的warp将有较大几率处于就绪态，系统就有可马上执行的warp，更好隐藏了延时.

    并行算法中工作组尺寸要划分合理，不同的工作组布局对存储器访问的性能是不同的.每个工作组的工作项数量应为warp size(32)的整数倍.这样可以提高访问全局存储器和本地存储器的效率.尽可能同时执行更多的工作项，以便隐藏存储器延时.本文设计的每个工作组中有192个工作项，这样有助于提高系统的执行效率.矩阵乘内核函数的工作空间设置为globalWorkSize[0]×globalWorkSize[1]，工作组内工作项值的大小为localWorkSize[0]×localWorkSize[1]，核函数的网格配置如下：

    • 1.3.3.   数据坐标变换

  • 在进行每个工作项的任务分配时，需要将矩阵子块中所有工作项在工作空间中的位置与一个矩阵元素对应处理.算法利用系统内建函数建立了工作项的ID索引workItemID如下.

    • 1.4.   针对GPU架构特性的优化

  • 在OpenCL计算模型中，系统定期从一个warp切换到另一个warp进行工作项调度，以最大限度利用计算单元的计算资源.如果32个工作项处于同一个warp中，则它们是被系统绑定在一起执行同一指令.所以，在每个工作组中包含的工作项总量应为32的整数倍，一般应保持在64至256之间，根据任务量的情况来确定工作组每个维度上的尺寸. 表 1中显示了矩阵大小为600×600，在工作组中设置不同数量工作项时的系统运行时间，从中可以看出当工作项为192时，系统性能最优.

2.   实验测试与分析

    2.1.   测试环境和数据记录

  • 硬件平台1：CPU为Intel Westmere E5690 2.4GHz(六核心)，系统内存为2.67GHz，12.0GB. GPU为NVIDIA Tesla K40，其中SM数为15，工作组中最大工作项数为1024，每个SM中最大激活工作项数为2048，每个SM中最大激活工作组数为16，每个SM中最大寄存器数为64KB，每个SM中最大本地存储器为16KB.

    硬件平台2：CPU为Intel Westmere E5690 2.4GHz(六核心)，系统内存为2.67GHz，12.0GB. GPU为AMD Radeon HD5870，核心频率为850MHz，总共1280个流处理器；显存采用频率为4.8GHz的GDDR5，容量为1000MB，位宽为256位.

    软件平台：Windows7 64位操作系统；Visual Studio 2015集成开发环境；并行开发环境为CUDA Toolkit 8.0，其内部支持OpenCL 1.2标准.

    实验采用矩阵规模大小分别为100×100，200×200，400×400，600×600，800×800，1 000×1 000，1 400×1 400共7组测试数据，矩阵乘法算法分别运行于基于单线程CPU串行系统、基于多线程CPU的OpenMP系统、基于NVIDIA GPU的CUDA系统、基于AMD GPU的OpenCL系统和基于NVIDIA GPU的OpenCL系统，并记录系统处理时间(表 2).

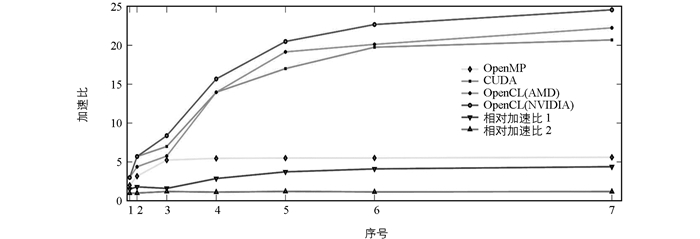
    为了对各种架构下的并行算法效率进行验证，将CPU串行算法执行时间与并行算法执行时间的比值(加速比)作为衡量加速效果的依据：基于多核CPU的OpenMP并行算法运算时间与基于NVIDIA GPU的OpenCL并行算法运算时间的比值是相对加速比1；基于NVIDIA GPU的CUDA并行算法运算时间与基于NVIDIA GPU的OpenCL并行算法运算时间的比值是相对加速比2.

    加速比反映了相应架构下并行算法相比CPU串行算法整体效率提升情况，可以用于对实际系统速度方面的客观评价(表 3).而相对加速比1可用于反映基于OpenCL的NVIDIA GPU并行算法相比基于多核CPU的OpenMP并行算法的效率提升效果，相对加速比2则可用于反映基于NVIDIA GPU的OpenCL并行算法相比基于GPU的CUDA并行算法的效率提升效果.

    • 2.2.   并行算法性能分析

  • 通过实验对基于NVIDIA GPU的OpenCL矩阵乘并行算法、基于AMD GPU的OpenCL矩阵乘并行算法、基于单核CPU的矩阵乘单线程算法、基于OpenMP的矩阵乘多线程算法和基于CUDA的矩阵乘并行算法进行对比. 表 2统计了各种算法在不同矩阵大小中进行矩阵乘法的运行时间.从表 2可知，单线程和多线程的CPU版本的运算时间最长，并且运算时间随矩阵规模的增加而明显增加.但是相比串行算法，OpenMP并行算法的执行时间增长更慢，获得了5.6倍的加速比.在CPU+GPU异构计算平台上运行的算法都有着较好的性能，实验中运算在各种矩阵规模下的矩阵乘算法均可在3s内完成.同时，随着矩阵规模的增加，CUDA加速的矩阵乘并行算法和OpenCL加速的矩阵乘并行算法的运行时间增加都较为平缓.

    由表 3数据可得图 2所示3种并行算法的加速比对比图.随着运算数据量的增大，基于GPU加速的矩阵乘并行算法相比OpenMP并行算法获得了更大的加速比，这是由于相比具有六核心的CPU，GPU可为大量数据的并行处理提供更充裕的计算资源和创建更多的工作项，从而获得的加速比较大.相对加速比2的曲线反映出基于OpenCL架构的并行算法相比基于CUDA的并行算法具有1.21倍的加速效果.这主要是因为系统通过预编译来加载算法内核时，采用了离线生成二进制文件的方法显著减少了应用初始化时间.

    当矩阵大小比较小时，系统启动的参与并行运算处理的工作项不多，并没有充分利用GPU中大量的CU.随着矩阵大小的扩大，系统启动的工作项数目在不断增多，算法获得的加速比也随着系统负荷的不断增加而扩大.当GPU的运算负荷接近饱和状态时，获得的加速比相应地也逐渐减缓.同时，CUDA加速的矩阵乘并行算法受制于硬件平台，OpenCL加速的矩阵乘并行算法分别在AMD GPU和NVIDIA GPU平台上取得了22.24倍和24.56倍加速比，说明在多种硬件平台上基于OpenCL的矩阵乘并行算法能够在最大程度上实现性能的可移植性和兼容性.

3.   结束语

  • 为使矩阵乘并行算法在异构处理平台下充分利用GPU的处理能力，本文针对OpenCL模型采用基于工作组和工作项两级并行计算方式，通过分析GPU构架特性，合理安排工作项组织结构，并对GPU的本地存储器的分配进行了优化.实验数据显示，与基于CPU的单线程算法、基于OpenMP多线程多核CPU并行算法和基于CUDA架构的并行算法相比，利用OpenCL加速的矩阵乘并行算法效率更高，实现了对大数据集的跨GPU计算平台实时处理.

参考文献 (20)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回