传统的跳跃表^[1]是典型的概率型数据结构，整个数据结构以多层有序链表形式呈现，其中上层结构的节点均会在下层结构的节点集中，可以认为上层节点由下层节点通过概率采样得到.

跳跃表设计目的在于对点查询和范围查询的良好支持，既可以根据查询条件中的查询起始点Firstkey进行点查询、又可以在定位到Firstkey后继续进行范围查询直到抵达终止点Endkey; 本文讨论的跳跃表查询操作(包含查询、插入、删除，以下均以Lookup查询操作指代)均指包含查询起始点Firstkey的操作.

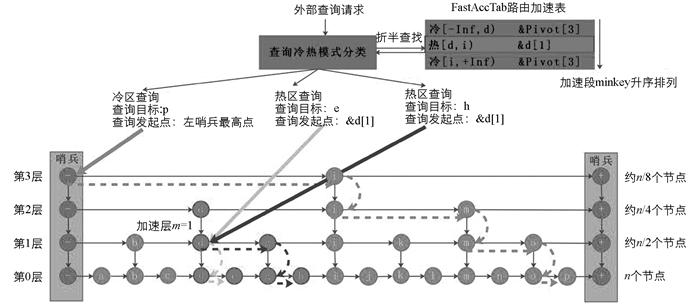
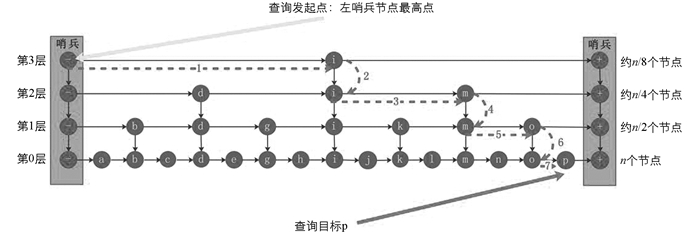
具体查询执行过程如图 1所示：

原生跳跃表在Lookup查询时，从数据结构的左上角(以下称为哨兵Pivot)出发，向右或向下逐步跳跃直至定位到查询目标或者无功而返.设以采样概率p构造的跳跃表节点规模为N，则其查询时间复杂度为O(Log_1/p(N))^[1]; 如果p=0.5，则跳跃表查询时间复杂度与红黑树相当(本文后续都假设该概率值p=0.5)为O(Log₂(N)).

众所周知，大数据库管理系统对性能的渴求远未抵达终点.对于以跳跃表为基础的内存索引来说，其加速的主要途径有两点：

其一是避免查询效率因随机因素退化.确定性跳跃表^[2]利用确定性技术替换随机概率生成方式，在更新跳跃表时同时调整目标节点附近的节点高度以维持事先定义的分布规则，单次更新影响的节点较多，不利于高并发场景的扩展; 最新研究成果如文献[3]将传统跳跃表改造为上下两层分层结构：下层由多个固定的半有序区段(称为GaurdEntity，区段间节点键值保证有序、区段内节点键值不保证有序)组成，用指向GaurdEntity的快速搜索结构(如FAST^[4])代替原生跳跃表上层链表，避免随机因素影响搜索效率.

其二是利用局部性原理.假设索引访问可能存在局部性，在访问热点设置快速路由，查询从传统左上角哨兵节点转而从热点附近的快速路由入口发起，旁路不必要的跳跃过程实现访问加速.文献[5]针对路由器管理的特定场景，将页面前缀和跳跃表节点地址分别做为哈希表的Key和Value，查询时先提取前缀，通过哈希表定位到对应前缀所在跳跃表节点附近再开始查找，提升查询性能.

本文基于局部性原理设计加速机制，能够根据工作负载情况选择热点进行路由，并根据加速情况和系统负载调整路由策略(层次、规模).

本文后续章节中，第二节从宏观层面上概述了热点敏感自适应跳跃表的整体架构和工作流程，阐述了热点加速和自适应调整的相互关系; 第三节具体阐述跳跃表的热点加速机制，包括与热点路由结合的跳跃表查询算法、跳跃表插入和删除算法的对应调整; 第四节阐述跳跃表加速策略的自适应调整机制和跳跃表热点路由的构建算法; 第五节给出相应实验和结论; 第六节总结了全文工作以及提出后续工作思路.

对于原生跳跃表来说，每个包括查询起始点Firstkey条件的Lookup查询请求q抵达时，需要从左上角哨兵节点最高层往下、往右跳跃去进行查找目标.

然而对于实际工作场景而言，Lookup访问模式往往存在局部性可供利用，即在一段时间内，大规模访问操作将会持续集中在某些区域，这就给加速提供了可能性.在热点区域附近设置快速路由入口，对热点区域的查询访问操作从快速路由入口发起而不是左上角哨兵节点发起，以此减少往下跳跃和向右跳跃的次数，从而实现查询加速; 对非热点区域的查询访问操作仍然从左上角哨兵节点发起.以上算法如图 2所示：

快速路由能够实现跳跃表查询加速，但有额外成本.每当新查询q抵达跳跃表时，都必须判断其是否落在某个热点加速段内并获取对应路由入口地址.这个路由表查询操作是范围查询，当热段和冷段的数目和是n时，每次路由表折半查询的时间复杂度是O(Log₂(n))，考虑到n远远小于跳跃表节点规模N，跳跃表的时间复杂度并未变化，但路由表查询耗时并不能忽视，路由表规模不能无限扩展.

对于原生跳跃表来说，每个包括查询起始点Firstkey条件的Lookup查询请求q抵达时，需要从左上角哨兵节点最高层往下、往右跳跃去进行查找目标，上述跳跃表加速技术需要数据分析的支撑，系统对跳跃表查询的执行过程进行记录，并定时分析以上查询执行信息以找到访问模式中的热点区域，刷新路由表.其中，热点区域的设置策略并非一成不变，需要根据加速效果和系统负载情况在线学习和演化.

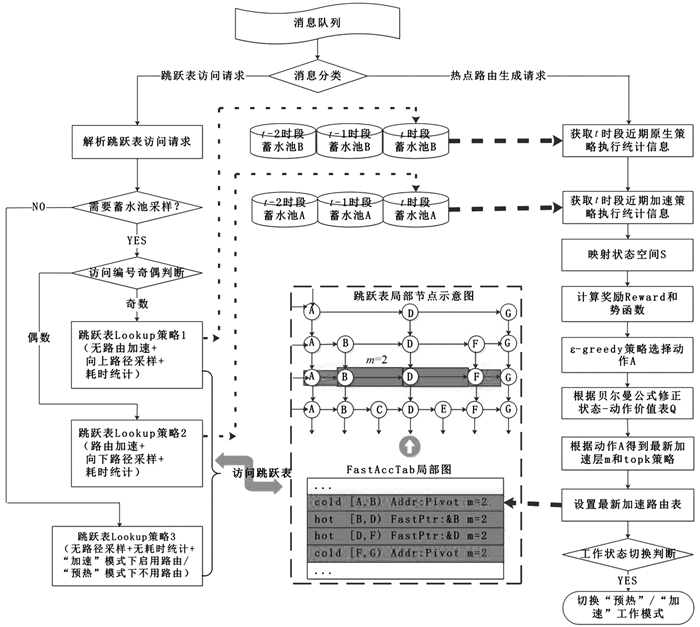
系统通过消息队列接收内外部消息，包括来自外部的跳跃表访问请求和来自内部定时触发的数据分析请求.热点敏感的自适应跳跃表工作流程图如图 3所示：

1) 对于来源于外部的跳跃表访问请求

如果查询条件中包含范围起始点Firstkey，本文将其定义为Lookup查询请求，后文将围绕Lookup查询请求进行讨论.系统将首先利用蓄水池采样^[6]技术对Lookup查询请求进行分流，再根据分流结果执行热点敏感的跳跃表查询算法HotRegionLookup，该算法中包含3种不同的Lookup查询操作策略(在3.1节中进一步阐述以上3种策略).此外，对于跳跃表访问请求中的删除操作，HotRegionLookup进行延迟删除(只设置删除标记、物理删除在数据分析周期内执行).

2) 对于内部定时触发的数据分析/路由表刷新请求

本文基于强化学习思想，将问题视为智能体与环境之间的互动，将环境视为外部查询访问操作的工作负载，智能体进行路由加速策略的选择.奖励则由实际加速效果、系统负载变化、加速机制对跳跃表结构影响综合而成.

每个数据分析周期都获取最近时间段的执行过程信息、评估当前系统的状态、核算即时和额外奖励、选择下一时段的加速策略并根据此策略进行加速路由表的刷新.在数据分析周期完成时，对不是路由点的待删除节点进行物理删除，若加速效果持续下降到达阈值，则关闭加速机制回到预热状态继续学习.

值得注意的是，由于强化学习是基于试探—奖惩的循环操作，在开始阶段往往不容易把握探索—利用之间的平衡，在本问题中将会造成不必要的性能颠簸以致影响关键系统的部署，因此本文针对强化学习系统的利用程度进行了控制.

① 初期系统工作在“预热(preheat)”模式.此时被蓄水池采样算法选中的查询请求执行HotRegionLookup策略1或者策略2，绝大多数其它查询请求执行HotRegionLookup策略3，从哨兵节点发起查询，且不记录执行过程和耗时，对整体系统的性能影响可控，此时根据策略1和策略2的执行情况进行强化学习，学习成熟后切换为“加速”模式.

② 系统工作在“加速(fullacc)”模式.此时被蓄水池采样算法选中的查询请求执行HotRegionLookup策略1或者策略2，绝大多数其它查询请求执行HotRegionLookup策略3，从快速路由表FastAccTab发起查询且不记录执行过程和耗时，充分利用强化学习的策略学习成果，此时根据策略1和策略2的执行情况继续强化学习，如果系统后续工作负载发生变化导致加速效果持续下降，则重新切换为“预热”模式.

由于跳跃表是大数据管理系统的关键索引结构，将某段时间内的访问操作全部记录进行分析将带来很大性能压力，因此需要利用采样技术提取访问操作记录的子集进行分析.

首先给出锚点定义：

定义    锚点Anchor(q，k)是Lookup访问操作q途经跳跃表第k层的下行节点.

如果一个节点是访问操作q在第k层的锚点，设其键值为key，其在k层的后继节点键值为keynext，根据跳跃表的访问逻辑，访问操作q的查询目标处于[key，keynext)区间内.

例如在图 1中，以“p”为目标的Lookup查询query在第3层锚点Anchor(query，3)的键是“i”，第2层锚点Anchor(query，2)的键是“m”，第1层锚点Anchor(query，1)的键是“o”.随着查询逐渐进行，由锚点标示的搜索空间从[“i”，+Inf)到[“m”，+Inf)和[“o”，+Inf)逐步缩小.

如上节所述，本文使用蓄水池采样进行操作采样，其能够保证每个操作被等概率选中，因此热点访问区域将会在蓄水池中高频出现.这里使用了双蓄水池A/B分别存储不同HotRegionLookup策略下的执行信息作为数据分析基础.

在本文所提出的加速方案中，加速路由点附着在第m层的某些符合要求的实际物理节点上，令当前加速层为m，不同的查询执行策略中，需要保存不同的执行信息.

① 路径高采样：在HotRegionLookup策略1中，记录查询q的耗时，该查询路径上处于m+3、m+2、m+1层的锚点信息，数据放入BasePool(蓄水池B);

② 路径低采样：在HotRegionLookup策略2中，记录查询q的耗时、该查询路径上处于m、m-1、m-2层的锚点信息，数据放入AccPool(蓄水池A).

① 首先给出区域的定义：

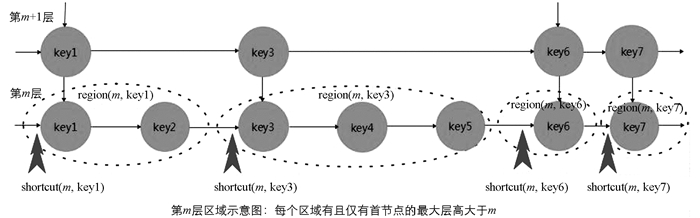
区域region(m，firstkey)：第m层区域region(m，firstkey)是跳跃表处于第m层某些连续节点的子集，令子集首节点为该子集中键值最小的节点，其键值为firstkey; 特别地该子集有且仅有首节点的最大层高大于m，该子集最后节点的后继节点是其它区域首节点.

区域之间的交集均为空; 令AllSearchSet为以跳跃表各个第0层节点为目标的全部原生查询操作合集，则全部区域的并集等于AllSearchSet中全部查询在第m层的锚点集合.

令AllRegionSet为跳跃表第m层全部区域的集合，nodes(r)为区域r的节点集合，则：

② 其次给出路由段的定义：

路由段segment(m，RegionList)：第m层路由段segment(m，RegionList)是跳跃表处于第m层某些连续区域的集合，RegionList中包含了该段中各个区域首节点的firstkey.路由段将由1个或多个完整区域region组成(热段仅包含1个完整region，冷段可能包含1到多个完整region).

令AllSegmentSet为跳跃表第m层全部路由段的集合，regions(s)为路由段s的区域集合，则：

令路由段segment的minkey是其区域集合中firstkey最小区域的首节点键值，令路由段segment的maxkey是其区域集合中firstkey最大区域最后节点的后继节点键值.

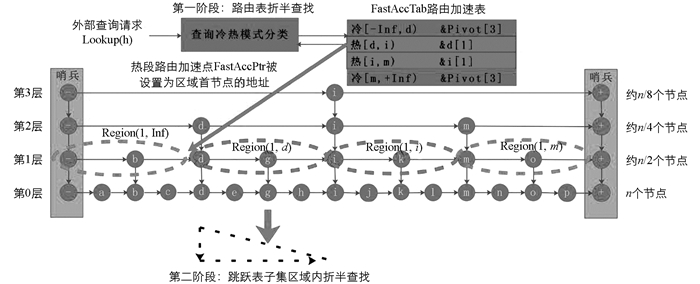
如图 4所示、路由加速表FastAccTab是一个结构体升序数组，数组中每个结构体元素代表一个路由段，包含如下信息：{Flag，[minkey，maxkey)，FastAccPtr，targetlevel}.其中Flag标示了该路由段的冷热性质，minkey是当前路由段首节点键值(以此升序)，maxkey是下个路由段首节点键值.如果该路由段是热段，FastAccPtr是对应路由加速点地址，否则为哨兵节点地址. targetlevel是加速点所在层数m，所有元素的该值均一致.

热点敏感的查询算法的算法逻辑如下：

1) 对于进入蓄水池且在蓄水池中编号为奇数的查询请求，执行HotRegionLookup策略1，查询从跳跃表最左哨兵节点发起并记录该查询的执行过程信息和耗时，将以上信息放入对应的缓存结构BasePool(简称蓄水池B);

2) 对于进入蓄水池且在蓄水池中编号为偶数的查询请求，执行HotRegionLookup策略2：查询从快速路由表FastAccTab发起(包含FastAccTab检索热点路由和后续查询执行)，向右向下搜索目标节点，并记录该查询的执行过程信息和耗时，将以上信息放入对应的缓存结构AccPool(简称蓄水池A);

3) 对于没有进入蓄水池的大部分查询请求，执行HotRegionLookup策略3，查询从最左哨兵节点(当系统处于“预热”模式)或者快速路由表FastAccTab(当系统处于“加速”模式)发起，向右向下搜索目标节点，不记录查询执行过程信息和耗时，以降低对性能的影响.

特别地，当查询从快速路由表FastAccTab发起时，首先折半查询FastAccTab中路由段数组segments，找到满足(s0.minkey＜=q＜s0.maxkey)条件的对应路由段s0;其次进行查询入口点设置：如果s0被标记为“冷”，则本次查询的入口点是哨兵节点，如果s0被标记为“热”，则本次查询的入口点是s0的对应FastAccPtr. FastAccPtr是该查询在第m层的锚点所在region的首节点地址，此处路由段的分配、冷热设置和对应FastAccPtr在路由刷新阶段会被提前写入到路由表中，具体在第4.2节的热区加速点分配算法HotRouterAllocate中有阐述.

综上所述，HotRegionLookup算法主要修改搜索入口地址，其向右向下搜索目标节点的过程与原生跳跃表算法中的Lookup执行过程^[1]保持一致，这里不再冗述.此外，HotRegionLookup需要对插入和删除操作做针对性调整.

由于引入了路由加速机制，跳跃表的删除和插入操作需要进行针对性处理和影响分析.

1) 删除操作分为逻辑标注和物理删除两个阶段.标准的Lookup访问操作只会执行逻辑标注，物理删除在每个数据分析周期结束后统一进行，物理删除操作将从最左上角哨兵节点发起，无视路由加速机制.

对于Lookup访问操作来说，如果判断某个节点的mask为逻辑删除，则继续利用其指针进行跳跃，只有在查询确定当前节点就是目标节点且mask标记为逻辑删除时，才根据查询/插入/更新/删除的不同操作目的，依靠可见性进行处理.

如果某个被逻辑删除的节点被设置成为路由点，则需要等待其失去路由点身份后才能进行物理删除操作，考虑到跳跃表能够维护的路由点规模有限，我们将其归结为额外的内存空间管理开销，并不视为内存泄露.

2) 插入操作和原生跳跃表插入操作存在差异：对于冷区数据的操作来说，与原生算法一致; 对于基于路由表进行加速访问的热区数据操作来说，插入节点的高度将不能高于加速层m.因为在路由加速机制下，系统无法低成本获取目标节点p在m层以上各层的前驱节点指针，本文将这种操作称为高度截断操作insert_level_cut，当m被压低时，该操作会破坏跳跃表的概率结构，需要在自适应算法中引入规避机制.因此这里插入截断操作的次数将被记录，支撑后续的自适应算法.

如前文所述，第0层节点规模为N的跳跃表以p=0.5概率逐层采样构成子链表.从原生跳跃表的Lookup查询执行过程可知，其搜索算法本质上是概率化的折半查询，因此原生跳跃表搜索的时间复杂度为O(Log₂N).

由4.2节阐述的HotRouterAllocate分配算法，会在第m层设置topk个路由加速热段，每段分配的路由加速点设置在热区首节点上.由于冷热间隔的原因，冷段最大规模是1+topk.因此FastAccTab的最大规模是1+2×topk.

这里假设跳跃表逐层以p=0.5采样概率构造子集，则第m+1层(0＜m＜=跳跃表最大层高d)的节点规模为N/2^m+1; 由于第m层每个区域有且仅有1个最大高度超过m的首节点，因此第m层有N/2^m+1个区域，以区域Region中节点为锚点的节点集合S平均规模是N/(N/2^m+1)=2^m+1.由跳跃表的性质可知，S其实是跳跃表的子集，从其在m层的首节点向右向下搜索，其时间复杂度是O(Log₂2^m+1)=O(m+1)=O(m).

由此可知，假设一个Lookup查询以概率p落入热段中，其查询时间的期望则为

采用HotRegionLookup算法基于原生跳跃表查询的吞吐量加速率(用η_ACC表示)为

由此可得出如下结论：

1) 落入热段的概率p越大，加速率越大;

2) 加速层高度m和加速段规模topk越大，加速率则越小;

3) 如果p×(O(Log₂N)-O(m))＜=O(Log₂(1+2×topk))，即落入加速段的查询加速量不能覆盖FastAccTab折半搜索新增的查询成本，则无法实现加速效果;

4) 在最理想的情况下(p=1所有查询访问均落入热点加速区域，topk=1仅有1个热区)，

此时能够取得非常高的吞吐量加速比.

但是，路由加速表的设置策略会影响热区命中率，因此概率p与m和topk隐含相关.不能一味地减少m和topk，否则会降低预测命中率p.

从第三节分析可知，决定跳跃表的加速性能的主要参数是加速点所在层次m和路由加速表热段的规模topk.对于实际场景下的不同工作负载，超参数很难有一劳永逸的设置.

首先介绍跳跃表的加速策略自适应算法，其次给出基于特定加速层的热区加速点分配算法.

这里将问题抽象为马尔科夫决策过程，从而基于强化学习思想进行求解.具体地将查询访问操作的工作负载视为环境，智能体进行路由加速策略选择，利用环境奖励的反馈机制评估不同状态下超参数设置策略的影响.周而复始，逐步实现从与环境的交互中学习到特定跳跃表在特定工作负载下的超参数设置策略.

首先，前文分析过超参数m的设置将影响到跳跃表插入操作，即高度截断操作insert_level_cut，该操作过于频繁有可能将跳跃表在m层以上的概率结构退化为链表，从而导致潜在性能问题.基于加速效果的奖励机制难以直接反映insert_level_cut影响，因此本文将insert_level_cut操作的最近次数与奖励重塑机制^[7]结合以提升强化学习效率.

其次，跳跃表作为大数据系统的关键数据结构，性能稳定性非常重要.在强化学习初期往往需要加强探索，导致策略的效果波动较大，并不适合直接运用在大规模负载查询中，此时没有进入蓄水池A/B的绝大多数查询q执行原生算法，只有进入蓄水池A的查询利用路由加速表FastAccTab，其加速性能与进入蓄水池B的原生查询进行对比，用来训练强化学习系统，称为“预热阶段”，当系统的稳定性和覆盖程度达到预设条件后切换到“加速阶段”.

进入“加速阶段”后，没有进入蓄水池A/B的绝大多数查询q利用路由加速表FastAccTab但并不进行计时和采样，通过蓄水池采样进入蓄水池A/B的查询继续训练强化学习系统; 如果随着时间流逝，加速效果持续低于原生算法达到阈值次数，说明跳跃表所依赖的可预测局部性已经失效，需关闭加速机制，重新切换回“预热阶段”，降低系统性能风险.

为了达到以上设计要求，本文基于SARSA算法^[8]思想进行算法设计.将状态空间离散化，再通过监控状态—动作价值表Q的变化情况和加速效果，决定从“预热阶段”到“加速阶段”的切换时机.

给出相关定义如下：

1) 定义t时段直接奖励reward：

这里Load(t)和Load(t-1)分别是t和t-1时段系统CPU负载指标，在奖励设计中综合考虑了加速效率和系统负载变化情况. duration(x)是操作x的执行耗时.

2) 定义t时段的势函数：

其中insert_cut_sum是当前时刻t所在状态S_t最近3个时间周期内对跳跃表insert操作的高度截断(insert_level_cut操作)次数之和，反映了加速机制对跳跃表结构的负面影响程度，应越低越好.

3) 定义ε-greedy动作选择策略：

令

4) 定义每时间段的状态—动作价值表更新算法，这里加入了奖励重塑机制：

令S_t-1为t-1时刻状态，A_t-1为t-1时刻动作; 令S_t为t时刻状态，通过公式(3)选择出动作a*作为A_t：

5) 定义状态空间S，共‖S1‖*‖S2‖*‖S3‖*‖S4‖*‖S5‖*‖S6‖个离散状态.

6) 定义动作空间，共6个离散动作：

7) 定义状态切换控制逻辑：

令Qt是Q表在t时刻的副本，Qt[s，*]表示t时刻状态s对应的状态—动作值向量a_vs.令max_rankpos函数返回该向量中最大值的位置maxpos;

定义辅助矩阵QMx，令QMx[t，s]=max_rankpos(Qt[s，*]); 即QMx的元素QMx[t，s]表示t时刻状态s下价值最高的动作编号. QMx[t，*]表示t时刻全部状态分别对应的最大价值动作的编号向量;

定义辅助矩阵USx，令USx[s，a]为Q表中对应元素的更新次数，min(USx[*，*])表示Q表中全部元素被更新的最少次数;

定义辅助列表RewardHistory，令RewardHistory[t]取值为强化学习系统在t时刻的即时奖励值; 定义列表LvlHistory，令LvlHistory[t]取值为t时刻的跳跃表加速层高度m.

如果满足公式(5)中的阈值C1/C2/C3和条件，即：t时刻Q表中全部元素都被充分更新覆盖，最近Q表各个状态对应的最大价值动作没有剧烈变化，系统通过蓄水池采样测量的加速效果稳定保持一定周期，系统将从“预热”切换到“加速”阶段：

令

如果满足公式(6)中的阈值C1和条件，即t时刻加速层在较高区间徘徊且系统通过蓄水池采样测量的加速效果不佳延续一定周期，系统从“加速”切换回到“预热”阶段.

令

综上所述，跳跃表自适应加速算法的逻辑流程如下(Q表在跳跃表建立时候被随机初始化)：

1) 获取当前时间段t内在蓄水池A/蓄水池B中的路径采样信息，根据表 1进行状态映射得到S_t;

2) 获取当前时间段t内在蓄水池A/蓄水池B中的耗时统计信息以及系统负载信息，根据公式(1)计算出时间段t的即时奖励reward(t);

3) 获取当前状态S_t和之前状态S_t-1的insert_cut_sum统计值，利用公式(2)计算奖励重塑的修正值;

4) 根据公式(3)中的ε-greedy动作选择策略，选择当前状态S_t下的动作A_t;

5) 根据公式(4)调整t-1时段下状态S_t-1和行为A_t-1在状态-动作价值表Q[S_t-1，A_t-1]的取值;

6) 执行当前选定的离散动作A_t：调整跳跃表的加速层m和热区规模topk选择策略;

7) 执行热区加速点分配算法HotRouterAllocate(在4.2节进一步阐述)，在跳跃表第m层上选择topk个热区，刷新路由表FastAccTab;

8) 进行系统工作状态切换判断：

① 若当前系统状态为“预热”且满足公式(5)中切换条件，将系统状态切换为“加速”;

② 若当前系统状态为“加速”且满足公式(6)中切换条件，将系统状态切换为“预热”，此时辅助统计量RewardHistory/LvlHistory/USx均重置，但Q表不会被重置.

从本质上来说，热区加速点设置是一个组合优化问题，目的在于基于工作负载的预测情况找到合适加速点取得合理加速效果.以上优化问题的搜索空间不能过大，如果加速点的可选范围是跳跃表全部节点，加速点规模设为topk，令跳跃表节点规模为S，则以上优化问题的解空间规模是C_S^topk，当跳跃表的规模在百万级以上时，求解空间将过于庞大以至于无法在可以接受的时间范围内完成搜索.本文对问题进行简化：将加速点的可选范围从跳跃表全体节点缩小到某一层m(m取值由4.1节强化学习所选择动作决定)，以减轻运算压力.

下面对热区加速点分配算法中的要素进行定义.

1) 定义区域捷径值shortcut(m，firstkey)：从跳跃表哨兵节点最高层到第m层区域region(m，firstkey)首节点的跳跃次数.如果加速点设置在某个m层区域的首节点firstkey，则所有经过该节点的访问操作都节约shortcut(m，firstkey)次跳跃.如图 5所示.

定义哈希表ShortcutHash为区域捷径的存储结构，通过区域首节点Firstkey访问.

2) 定义节点工作负载Workload(m，t，key)：在t时间段内，经过跳跃表第m层键值为key的节点下行访问计数值.从以上定义可知：节点工作负载Workload是该时间段内访问操作落在其与后继节点间的频数，也就是该节点作为第m层锚点的查询路径出现频数.

这里的节点工作负载需要通过现有负载对未来进行预测，例如BP神经网络^[10]、LSTM^[11]、SVR^[12]; 考虑到跳跃表节点规模可能非常大，百万规模跳跃表中间层包含的节点数目就高达数万，为每个节点维护独立的时间序列预测模型将会带来很大运算压力，本文给加速层m中每个节点采用二阶指数平滑算法^[13]做负载预测，以追求预测精度与时效性之间平衡.

定义哈希表HitHash(形如HitHash＜key，Workload＞)为节点工作负载的存储结构，通过key访问.

3) 定义区域价值RegionValue(m，t，firstkey)：当加速点设置在firstkey上，在t时间段内，跳跃表第m层以firstkey为首节点键值区域r减少的跳跃次数.

令PtDis(m，key1，key2)为跳跃表第m层键值分别为key1、key2节点之间跳跃间隔.

定义哈希表RegionValHash(形如〈Firstkey，RegionValue〉)为区域价值的存储结构，通过区域首节点Firstkey访问.

下面对热区加速点分配算法HotRouterAllocate进行阐述，算法基于如下两点考虑：

一是任何被选中的热点区域，有且只有一个加速点被设置用来对本区域的节点访问进行加速，简而言之，热点区域将不会被分割.以上策略保证热区加速点的宝贵资源能够充分利用，让尽量多的热点区域能够被选中进行加速，从实际效果来看，本文工作将该加速点设为区域首节点，具有更强的适应性.

二是跳跃表特定层的热点区域规模不应该过大，针对特定跳跃表的特定工作负载，在特定层热点区域规模也难以由人为预先指定，因此热点区域规模需要尽可能基于工作负载实际分布得出，此处逻辑由4.1节强化学习所选择动作的“Tidy”或者“Common”策略决定.

综上所述，HotRouterAllocate算法逻辑流程如下：

1) 对跳跃表m层中每个区域，计算每个区域shortcut，依次放入ShortcutHash;

2) 对跳跃表m层中每个区域的各个节点p，利用之前AccPool/BasePool蓄水池中采样数据，采用指数平滑算法预测该节点后续工作负载workload(m，t+1，p)，并依次放入HitHash;

3) 对跳跃表m层中每个区域，根据公式(7)结合HitHash和ShortcutHash计算每个区域的价值RegionValue，并依次放入RegionValHash; 遍历哈希表RegionValHash，将其中各个元素的区域价值插入数组RValVec; 令mvv=median(RValVec)，rvv=std(RValVec);

4) 确定热区规模topk：利用聚类算法来提取一维工作负载数据分布的内在规律，考虑到效率因素，本文采用划分聚类k-means^[14]来确定较大价值的热点区域规模，而非更高精度但耗时的聚类算法如PAM算法或者dbscan密度聚类.

① 若topk设置策略为“Common”：令SubDs0=RegionValVec中取值超过中位数mvv的全部元素集合，设置topk=|SubDs0|;

② 若topk设置策略为“Tidy”：首先抽取RegionValVec中取值大于(mvv+rvv)的元素到集合SubDs1、其次对RegionValVec中取值在[mvv-rvv，mvv+rvv]范围的元素进行二分k-means划分聚类，令中心值较高的聚簇为SubDs2，设置topk=|SubDs1|+|SubDs2|.

5) 刷新路由加速表FastAccTab：选择哈希表RegionValHash中取值最大的topk个元素所在region构成热段，每个热段的入口点FastAccPtr设置为对应region所在firstkey的地址; 未被选中的区域被热段分割成为冷段，保持冷热段的minkey呈现升序排列插入FastAccTab-＞segments，完成FastAccTab刷新.

实验环境采用1台DELL R730服务器，256G内存，2颗Intel Xeon E5-2680 v4规格CPU，每颗处理器有14个核心.实验环境CPU总体负载指标保持在10左右，模拟系统遭遇中等程度服务压力.其中强化学习的学习率λ设置为0.1，折扣率φ设置为0.5，探索率ε设置为0.1，C1=10，C2=0.8，C3=6.为了验证本文所提出的加速算法和自适应机制，给出如下实验结论.

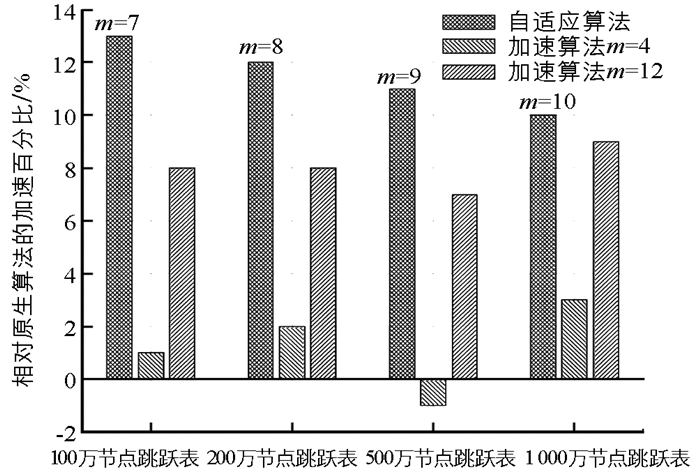
目的在于验证访问压力倾斜和波动幅度较低的场景下，本文方法的加速有效性.本实验有4个规模不同的24层跳跃表，分别有100，200，500，1 000万规模，节点键值类型是8字节长整形.

1) 局部性弱的场景(50%随机、50%压力集中在20%区域形成512个正态分布，各个热点区域中心每个周期随机左右移动1/8个热区范围标准差)测试：

此时访问负载较为分散，为了尽量捕捉负载热点就需要提升topk.这种情况下m无论过高(m=12，shortcut利用率不高)或者过低(m=4，过多topk增加了路由搜索消耗，存在加速失败的情况)都不能有效工作.自适应算法在不同规模跳跃表停留在不同层次上(m=7/8/9/10)，能够达到相对稳定的加速效果.

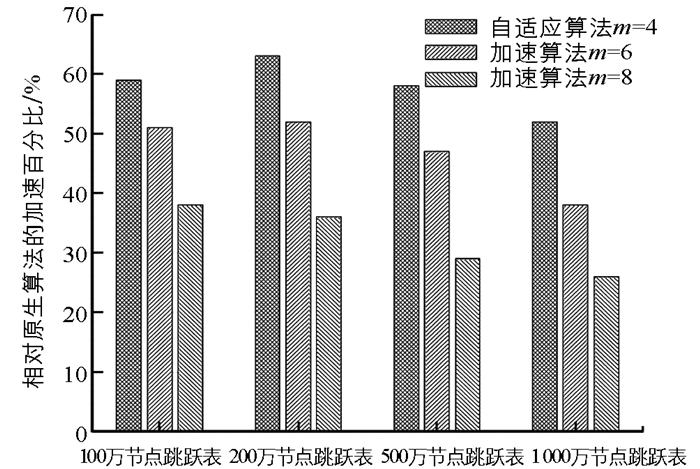
2) 局部性强的场景(20%随机、80%压力集中在20%区域形成64个正态分布，各个热点区域中心每个周期随机左右移动1/8个热区范围标准差，模拟访问压力重度倾斜)测试：

此时访问负载较为集中(topk无需过大)且可预测性较好，总的来说局部性较强，采用路由加速算法都可以达到性能提升的效果，此时自适应算法尽量驻留在了较低层次(m=4)以提升shortcut利用率，能够达到稳定和高效的加速效果.

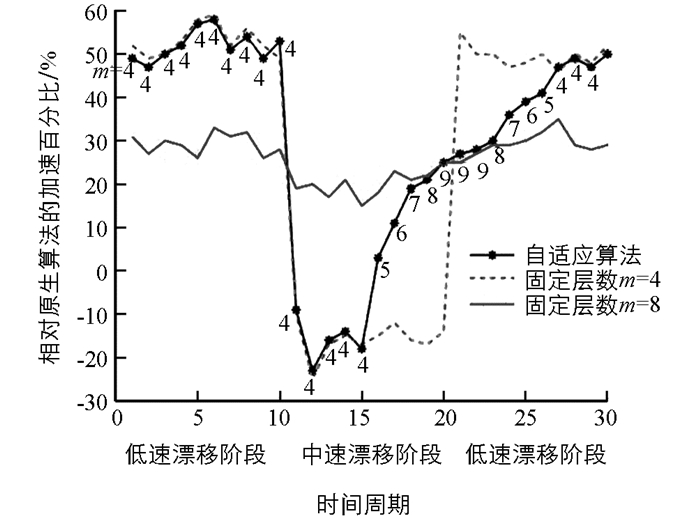
目的在于验证加速策略针对访问热点波动的自适应能力，自适应机制每隔1个时间段(15 s)启动一次调整加速策略. 图 8和图 9是工作负载漂移场景下加速策略性能：

1) 工作负载中速漂移的场景测试结论. 24层200万节点规模跳跃表，节点键值类型是8字节长整形，访问压力重度倾斜，64个热点区域中心每个周期随机左右平移：1~10时段1/4个热区范围标准差; 11~20时段1/2个热区范围标准差; 21~30时段1/4个热区范围标准差.

该结果说明：当工作负载变化存在可预测性时，自适应算法的灵活性优于原生算法和加速层固定的算法.在1~10阶段负载集中且波动率较低，此时m=4停留在较低层提升shortcut利用率; 在11~20阶段负载波动率增强，m呈现上涨趋势以提升预测命中率; 在21~30阶段负载波动又下降，m也随之下降以提升shortcut利用率，说明在这里利用强化学习可以从环境中充分学习，找到适合工作负载的超参数设置策略.

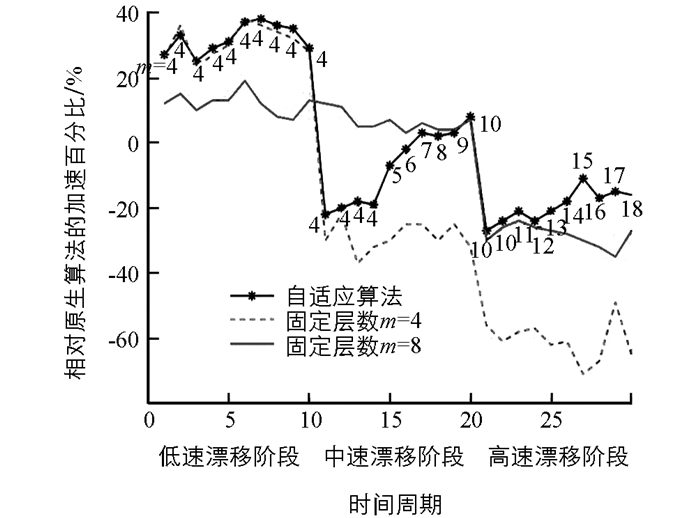
2) 工作负载高速漂移的场景测试结论. 24层200万节点规模跳跃表，节点键值类型是8字节长整形.访问压力重度倾斜，64个热点区域中心每个周期随机左右平移：1~10时段1/4个热区范围标准差; 11~20时段1/2个热区范围标准差; 21~30时段1个热区范围标准差.

该结果说明：当工作负载的波动逐渐增强时，对热点的可预测性逐渐降低，此时基于局部性原理的算法均存在性能下降的问题，但自适应跳跃表能够充分感知环境变化(m值在持续上涨以尽量捕捉热点)，及时切换加速机制(根据公式(6)，200万规模的24层跳跃表在m＞=16且加速失败情况持续一段时间后，将达到切换条件)以稳定整体性能、节约运算资源.

本文针对跳跃表性能优化的自适应机制进行了初步的探索，具体研究了利用局部性原理提升跳跃表查询效率的问题.首先利用跳跃表本身的结构特点，结合工作负载预测技术设计了基于热点的路由加速机制; 其次根据加速的实际效果和管理资源的消耗情况，设计了基于强化学习的自适应机制来动态调整加速点的所在层次.后续工作目标是去掉加速点保持在同一层的约束，不同热点区域的路由加速点由对应热点区域的变化幅度和变化频率自主决定.一是需要研究更有效的针对性搜索算法以减少搜索的计算压力，目前基于同一层的加速点选择算法可以作为进一步工作的基础; 二是既然加速机制由集中控制变为分散控制，自管理模式也需要随之变化，需要考虑多智能体强化学习与以上加速机制的结合方式.