下面介绍混合高斯模型及其性质、几何平均亚式幂期权的回报函数等相关概念.

定义1^[15]  设(Ω，F，P)是一个完备的概率空间，混合高斯模型M_t^H定义为

其中：a，b是常数且(a，b)≠(0，0)，H∈(0，1)为Hurst指数，ξ_t为标准布朗运动，ξ_t^H为次分数布朗运动且ξ_t与ξ_t^H相互独立.

混合高斯模型M_t^H，∀t≥0具有如下性质^[15]

1) M_t^H是一个中心高斯过程；

2) $ M_0^H = a{\xi _0} + a\xi _0^H = 0 $；

3) $ \forall s\in {{\mathbb{R}}_{+}}, \forall t\in {{\mathbb{R}}_{+}} $与M_s^H的协方差函数为

其中$ s\wedge t=\frac{1}{2}\left( s+t-\left| s-t \right| \right) $.

下面给出亚式幂期权回报函数相关的概念.

定义2^[16]  固定行权价格为K，连续观测情形下几何平均亚式幂期权的回报函数为

其中$ n\in {{\mathbb{Z}}_{+}} $，A_t表示价格S_t在[0，t]之间的几何平均值，且

记

假设标的资产价格满足如下随机微分方程

其中：μ，q，σ均为常数，分别表示股票的预期收益率、股票的红利率、股票价格的波动率，M_t=aξ_t+bξ_t^H是混合高斯过程. 不失一般性，取a=b=1进行讨论. Q_t=N_t-λt是补偿泊松过程，N_t是强度为λ的泊松过程，且ξ_t，ξ_t^H，N_t相互独立.

定理1(混合高斯跳过程Itô公式) 设X_t=ξ_t+ξ_t^H+Q_t为混合高斯跳过程，f(t，x)具有连续的一阶以及二阶偏导数，那么

证  任意给定ω∈Ω，从而固定了过程X_t=ξ_t+ξ_t^H+Q_t的路径.

设0=t₀ < t₁ < t₂ < … < t_n-1 < t_n=t是该路径在[0，t)内所有发生跳跃的时刻(t₀除外). 记Q_t在t_i时刻发生第i次跳跃，则当i=1时，在[0，t)内只发生一次跳跃，且跳跃发生的时刻为t₁，即X_t在[0，t₁)与(t₁，t)内没有发生跳跃则在[0，t₁)与(t₁，t)内分别用分数型Itô公式可得

因X_t在时刻t₁发生$ {{X}_{t_{1}^{-}}} $到$ {{X}_{{{t}_{1}}}} $的跳跃，则f(t，X_t)在t₁时刻的变化量为$ f\left( {{t}_{1}}, {{X}_{{{t}_{1}}}} \right)-f\left( {{t}_{1}}, {{X}_{t_{1}^{-}}} \right) $，故

现在考虑在[0，t)内所有的跳跃时刻t_i(i=1，2，…，n)，则有

设$ g\left( s \right)\in {{C}^{2}}\left( \mathbb{R}\to \mathbb{R} \right) $，由于(dN_t，dN_t)=λdt，对g(N_t)应用广义Itô积分^[11]，有

因X_t=ξ_t+ξ_t^H+N_t-λt，则

将(3)式带入f(t，X_t)的表达式得

证毕.

由定理1可得如下推论.

推论1  随机微分方程(1)的解是

定理2  假设标的资产价格S_t满足混合高斯跳过程驱动的随机微分方程(1)，则行权价格为K，到期日为T的几何平均看涨亚式幂期权在t(0≤t≤T)时刻的价格V_c(t，S_t，G_t)满足如下的偏微分方程

其中0 < S_t < ∞，0 < G_t < ∞，δ²=σ²[1+λ+2Ht^2H-1(2-2^2H-1)]，边界条件为

证  设A_t为标的资产价格在[0，t]上的几何平均值，即

令

则

假设在金融市场上交易两种资产，一种是无风险资产，比如债券；另一种是有风险资产，比如股票. 债券价格P_t和股票价格S_t分别满足下列微分方程

其中r为无风险利率.

考虑一个自融资投资策略θ=(θ_t⁰，θ_t¹)，则其资产价值为$ {{V}_{t}}=\theta _{t}^{0}{{P}_{t}}+\theta _{t}^{1}{{S}_{t}} $，又因股票需要连续支付股息q，故

将(6)式带入(7)式可得

另外，由定理1和推论1可得

由无风险套利原理可知：期权价值与投资组合θ=(θ_t⁰，θ_t¹)的价值相等，故令$ \theta _{t}^{1}=\frac{\partial V}{\partial {{S}_{t}}} $，则可以对冲包含风险的项dX_t. 于是

经过整理可得

令δ²=σ²[1+λ+2Ht^2H-1(2-2^2H-1)]，从而

证毕.

定理3  假设标的资产价格S_t满足混合高斯跳过程驱动的随机微分方程(1)，则行权价格为K，到期日为T的几何平均看涨亚式幂期权在t(0≤t≤T)时刻的价格V_c(t，S_t，G_t)为

其中

证  由定理2可知，在t(0≤t≤T)时刻的价格V_c(t，S_t，G_t)满足偏微分方程(5). 令

则

那么偏微分方程(5)可以转化为

令

其中α(t)，β(t)，γ(t)为待定函数，则

带入(9)式，整理后得

再令

由终止条件α(T)=β(T)=γ(T)=0解得

则(10)式可化为

根据热传导方程经典理论，其存在唯一强解，从而

分别计算I₁和I₂.

令$ \frac{y-{{\eta }_{\tau }}-2\tau }{\sqrt{2\tau }}=t $

同理令$ \frac{y-{{\eta }_{\tau }}}{\sqrt{2\tau }}=t $

综上可得(11)式的解为

其中

所以由U(t，φ_t)和X(τ，η_τ)之间的关系得

证毕.

推论2  假设标的资产价格S_t满足混合高斯跳过程驱动的随机微分方程(1)，则行权价格为K，到期日为T的几何平均看跌亚式幂期权在t(0≤t≤T)时刻的价格V_p(t，S_t，G_t)为

推论2的证明与定理3类似，且其中β(t)，τ，η_τ，d₁，d₂与定理3相同.

根据定理3和推论2中的几何平均亚式幂期权看涨以及看跌公式进行数值模拟，讨论定价公式中各参数对于期权价格的影响. 对于一份基于(1)式的几何平均亚式幂期权，考虑当期权定价公式中一些参数给定的条件下，某一参数的变化对于期权价格的影响.

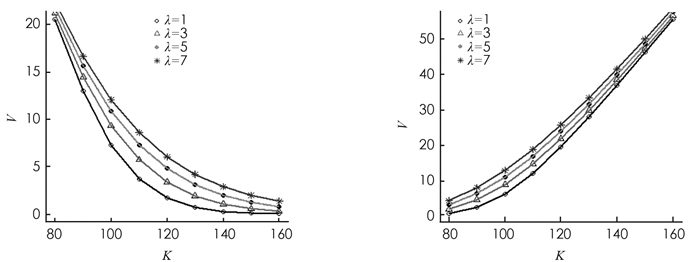
第一，研究跳跃强度λ的大小对于期权价格的影响程度. 假设标的资产(股票)当前价格S=100，无风险利率r=0.06，红利率q=0.02、股价波动率σ=0.2，n=1，Hurst指数H=0.75，到期日T=1，当前时刻t=0.图 1分别给出了在泊松过程的不同跳跃强度下，行权价格与看涨以及看跌期权价格之间的关系. 从图 1可以看出，对于给定的行权价格，跳跃强度越大，看涨期权和看跌期权的价格均越高.

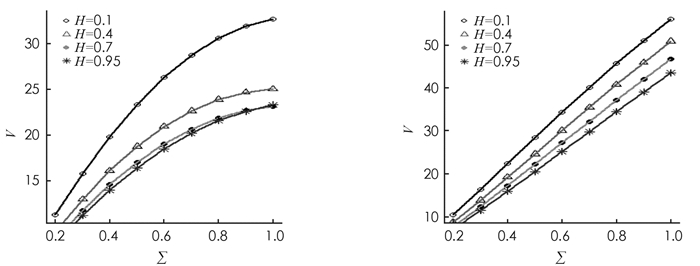
第二，研究Hurst指数H对于期权价格的影响. 假设S=100，K=100，r=0.06，q=0.02，λ=2，n=1，T=1，t=0. 图 2分别给出了在不同的Hurst指数H下，波动率与期权价格之间的关系. 从图 2可以看出，对于给定的波动率，H越大，看涨、看跌期权的价格越小；对于不同的H，随着波动率的增大，看涨、看跌期权价格均上升，但是上升的趋势略有不同.

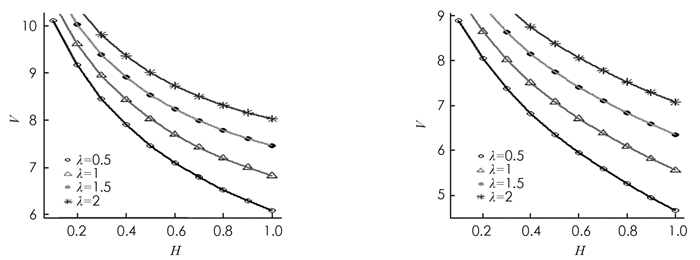
第三，研究Hurst指数H与跳跃强度λ对期权价格的影响. 假设S=100，K=100，r=0.06，σ=0.2，q=0.02，n=1，T=1，t=0. 图 3分别给出了对于不同跳跃强度的大小，随着Hurst指数H的增加，看涨、看跌期权价格的变化情况. 从图 3中可以看出，对于给定的H，跳跃强度越大，看涨、看跌期权价格越高；随着H的增大，对于不同的跳跃强度，看涨、看跌期权价格均下降，且跳跃强度越大，价格下降越缓慢.

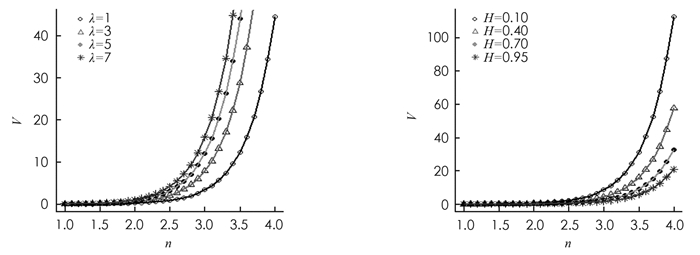
第四，研究n的变化对于期权价格的影响(以看跌期权为例). 假设S=10，K=10，r=0.06，σ=0.02，q=0.02，T=1，t=0. 图 4分别给出了跳跃强度与n、Hurst指数H与n对看跌期权价格的影响. 从图 4中可以看出，当n超过某一阈值时，n的增大会对期权价格产生显著影响，这充分体现了幂期权的杠杆效应.

通过假设标的资产价格变动由混合高斯跳过程描述，比较全面地考虑了金融资产价格的运动行为. 运用分数型Itô公式推导出了混合高斯跳过程Itô公式，并运用自融资策略以及风险中性原理得到了几何平均亚式幂期权价格所遵从的数学模型，得到几何平均亚式幂期权的看涨、看跌公式. 最后通过数值模拟验证了Hurst指数H、跳跃强度λ以及幂次n对期权价格有显著影响. 该结论是对已有研究结果的推广，丰富了奇异期权产品创新的理论依据.