定义1  对任意常数α＞0和β∈$\mathbb{R}$，Mittag-Leffler函数定义为

引理1^[21]  若0＜α＜1，对于任意的λ_n都有λ_n≥λ₁＞0，则存在正常数C使得

其中C=1-E_α，1(-λ₁T^α).

引理2^[22]  如果q(t)∈$\mathbb{C}$[0，T]满足：对∀t∈[0，T]，都有q(t)≥q₀＞0，令

则有

引理3^[23]  对0＜λ＜1，定义$p_{k}(\lambda)=\sum\limits_{i=0}^{k-1}(1-\lambda)^{i}$和r_k(λ)=1-p_k(λ)λ=(1-λ)^k，则有

其中

假如初边值条件和源项都是已知条件，则通过分离变量法以及Mittag-Leffler函数的Laplace变换可得到正问题(1)的解u(r，t)如下

其中：φ_n=(φ(r)，ω_n(r))，f_n=(f(r)，ω_n(r))，$\lambda_{n}=\left(\frac{n \pi}{R}\right)^{2}, \omega_{n}(r)=\frac{\sqrt{2}}{r \sqrt{R}} \sin \left(\frac{n \pi r}{R}\right)$，n=1，2，…. 这里的ω_n(r)是在区间[0，R]上带权r²的标准正交函数系，它可以构成一个完备系统，且有(f(r)，ω_n(r))=$\int_{0}^{R} r^{2} f(r) \omega_{n}(r) \mathrm{d} r$.

利用终值数据u(r，T)=g(r)可得

其中g_n=(g(r)，ω_n(r)).

记

并定义算子K：f(r)→h(r)，则有

可知算子K是一个具有奇异值

和特征函数ω_n(r)的线性自伴算子. 根据ω_n(r)的性质，式(5)可改写为

所以有

根据引理2可知

这表明终值数据g(r)中的微小扰动都会导致源项f(r)发生巨大变化，亦即该逆源问题是不适定的. 因此需要通过正则化方法来恢复解的稳定性.

为了保证解的稳定性，假设源项f(r)满足先验界条件

这里范数‖f(·)‖_p的定义为

定理1  若f(r)满足‖f(·)‖_p≤E，则有

其中

证  由Hölder不等式和式(6)，有

根据引理2，则有

所以由式(8)，(9)可得

注1  根据定理1的证明，可以类似得到

这意味着可以通过估计‖f‖_p和‖Kf‖的L²范数来得到f的L²范数的界.

本节将通过迭代正则化方法求得源项f(r)的正则近似解，并分别给出先验和后验参数选取规则下精确解与正则近似解之间的误差估计.

我们通过构造如下正问题来逼近原来的逆源问题，这里u^k(r，t)是如下问题的解

其中源项f^k，δ(r)通过下面的迭代方式给出，

这里s是一个加速因子，它满足：对∀n∈$\mathbb{N}$，有

k是迭代步数，它相当于正则化参数.

不妨记

则易得

根据式(10)有

定理2  设f(r)是逆源问题的精确解，f^k，δ(r)是由式(11)给出的正则近似解，若先验界条件(7)和假设(2)都成立，并选取正则化参数

则可得到如下误差估计

这里$C_{1}=\frac{R^{2} q_{0} \bar{C}}{\pi^{2}}$，[m]表示不大于m的最大整数.

证  由三角不等式，有

根据式(11)，(2)和(3)，并取μ=0，可得

由先验界条件(7)、引理2和式(4)，取$v=\frac{p}{2}$，则有

结合式(13)和(14)，并选取

即可得到

设τ＞1为给定的常数，正则化参数k的取法是满足下面偏差原理

定理3  设f(r)是逆源问题的精确解，f^k，δ(r)是由式(11)给出的正则近似解，若先验界条件(7)和假设(2)都成立，且正则化参数k由式(15)取定，则可得到如下误差估计

证  由三角不等式，有

由式(13)知

由式(15)可得

故有

将式(17)代入式(16)，得

另一方面，

根据f(r)的先验界条件以及范数‖f(·)‖_p的定义，有

应用注1，可得

结合式(18)和式(19)，即可得到所要结果.

通过数值算例验证迭代正则化方法对处理球对称区域上分数阶扩散方程逆源问题的有效性. 由于正问题(1)的精确解很难获得，故利用有限差分法求解正问题. 通过给定的函数φ(r)，q(t)和f(r)，来获得终值数据g(r). 在数值试验中，我们取R=3，T=1，时间和空间上等距划分的份数分别为M=100，N=50，相对应的步长分别为$\Delta t=\frac{T}{M} \text { 和 } h=\frac{R}{N}$，并记t_n=nΔt(n=0，1，…，M)，r_i=ih(i=0，1，…，N)，每个网格点处的值为u_iⁿ≈u(r_i，t_n). 先验规则下的正则化参数k由式(12)给出，后验规则下的k通过式(15)计算得到，其中τ=1.1.

时间项导数可以通过Caputo分数阶导数的L₁插值逼近来近似得到

其中a_l^(α)=(l+1)^1-α-l^1-α，l≥0.

空间项导数由如下格式近似得到

对有限差分得到的终值数据g(r)按如下方式添加随机扰动得到噪声数据：

其中ε＞0反映相对误差水平，相应的噪声水平为δ=‖g^δ-g‖.

为了说明正则近似解的精确性，我们计算绝对误差

和相对误差

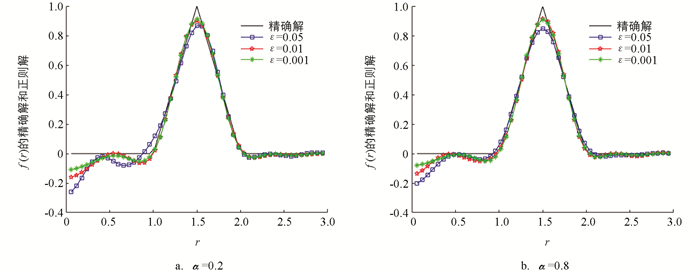
例1  取函数q(t)=2t+π，φ(r)=sin(r)，精确的源项为

图 1和图 2分别给出了先验和后验正则化参数选取规则下，取α=0.2，0.8时不同误差水平下的正则近似解与精确解的数值结果. 在表 1和表 2中，我们分别给出先验和后验规则下ε=0.01，α取不同值时精确解与正则近似解之间的误差分析以及α=0.5，ε取不同值时精确解与正则近似解之间的误差分析.

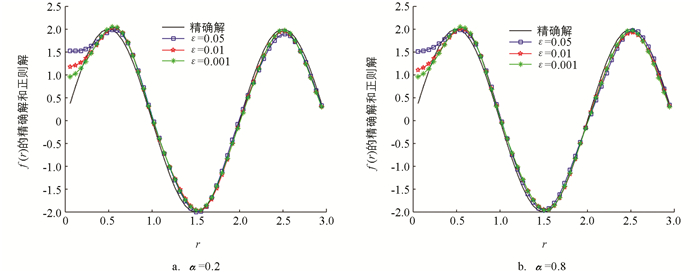
例2  取函数q(t)=t+6π，φ(r)=r²-4r，精确的源项为

在图 3和图 4中，我们分别给出了先验和后验规则下，取α=0.2，0.8时不同误差水平下的正则近似解与精确解之间的数值结果. 在表 3和表 4中，我们分别给出先验和后验规则下，ε=0.01，α取不同值时精确解与正则近似解之间的误差分析以及α=0.5，ε取不同值时精确解与正则近似解之间的误差分析.

综合对比图 1至图 4，可以看出，后验正则化参数选取规则下重构的源项与精确解之间的拟合效果总体要比先验的好一些. 再结合表 1至表 4，可以发现数值误差关于α变化比较稳定，故我们的方法对α不太敏感(这与文献[20]的结果相符)，同时也可以发现随着随机扰动ε的减小，数值误差明显在减小，精确解与正则近似解也越来越吻合. 这说明对于球对称区域上分阶扩散方程的逆源问题，采用该迭代正则化方法有着非常好的效果.

探讨了球对称区域上分数阶扩散方程逆源问题. 通过迭代正则化求得源项的正则近似解，并在先验和后验参数选取规则下给出了精确解与正则近似解之间的Hölder型误差估计. 最后，通过数值算例验证了该迭代方法处理此逆源问题的有效性.