给定超图H=〈V，E〉，其中V={v₁，…，v_n}，是n个节点组成的节点集，E={e₁，…，e_m}，是由m个超边组成的超边集. 每一条超边e_j由若干个节点组成，表示节点之间的相互作用，用|e_j|表示超边e_j的大小，即其所包含的节点数. V的所有节点组合构成了该节点集的幂集2^V，取节点组e∈2^V，则e的大小可取值1，2，3，…，n. 因此有超图的超边集E⊂2^V. 数学上，使用关联矩阵B=(b_ij)_n×m表示超图，其行表示节点，列表示超边，当且仅当节点v_i属于(亦称关联)超边e_j时，对应元素b_ij=1，否则b_ij=0.

对于上述超图，想象因“某种原因”使得部分超边丢失，导致其仅有部分超边能够被观察到. 则E被分为已观察超边集E^o(亦称正边集)和遗失超边集E^uo，且有E^uo=E\E^o，这些遗失超边与不能够形成超边的节点组(亦称负边集)混杂在一起组成了候选集D，记负边集合为Eⁿ，且有D=E^uo∪Eⁿ，Φ=E^uo∩Eⁿ. 基于此定义超图上的链路预测任务：利用正边集E^o，从候选集D中尽可能多地寻找到属于E^uo的边. 该任务等价于一个二分类问题，在实施过程中，首先利用链路预测方法对D中所有样本进行评分，根据评分结果设立一个阈值，将评分高于阈值的样本判定为正样本，否则为负样本.

这里，候选样本集E^s的选取也值得讨论. 在超图链路预测的环境下，超边大小的任意性导致了候选集(所有未形成边的节点组)2^V\E^o的大小呈O(2^|V|)上升，即所谓的“极端类不平稳问题”(extreme class imbalance，简称ECI)^[2]. 从大量的候选边中寻找各个遗失超边无异于大海捞针. 为此，需要对候选集进行下采样以减小推断空间的大小. 而下采样所采样出的候选样本需要符合“实际情况”，这里将“实际情况”理解为候选样本的大小分布应该与已观察超边集合的大小分布一致^[2]. 为此，根据已观察超边集E^o的超边大小分布，对候选样本空间2^V\E^o进行下采样以生成候选样本集E^s，从而保证候选样本集E^s的大小分布与E^o一致.

超链路预测问题考虑的是超图中一组节点是否能形成超边，因此首先研究节点对之间的相似性. 本文提出用超图上带重启的随机游走来定义节点对之间的相似性，还拓展了基于普通图的一些节点对相似性方法来定义超图中节点对的相似性. 基于节点对的相似性再刻画节点组的相似性，以此作为超链路的预测方法.

带重启的随机游走是链路预测里的一个经典方法，该方法基于图上的带重启随机游走，并将节点对之间的平稳互达概率作为链路预测分数^[11]. 为将上述指标扩展到超图，需要先定义超图上的随机游走. 假设游走者在时刻t(t=0，1，…)位于节点v_i，考虑一种无偏的情况，游走者首先随机游走到包含该节点的任意一条超边上，并在t+1时刻随机游走到关联该超边的节点v_j. 这里定义的超图随机游走可简单表述为上述过程的迭代. 该游走者在t到t+1期间，从节点v_i转移到节点v_j的概率为：

式(1)计算了从v_i到v_j的单步转移概率，其前一项和后一项分别描述了“游走到超边”和“游走到节点”的过程. 由于超图中有n个节点，相应地有n²个单步转移概率，将这些概率值组织成概率转移矩阵P=(p_ij)_n×n. 依式(1)可将该矩阵进行分解：

$\boldsymbol{D}_{v E} \in \mathbb{R}^{n \times n}, \boldsymbol{D}_{e V} \in \mathbb{R}^{m \times m}$，均为对角阵，对角线元素分别为各节点所关联的超边数和各超边所包含的节点数.

定义状态向量$\boldsymbol{\pi}_t^i \in \mathbb{R}^{n \times 1}$，其第j个元素π_tⁱ[j]表示初始时游走者在节点v_i，经过t步随机游走后位于节点v_j的概率. 显然，该向量表示了一个随机分布，满足$\sum\limits_{k = 1}^n {\boldsymbol{\pi} _t^i} [k] = 1$. 由于初始时游走者具有确定的位置状态v_i，初始状态向量π₀ⁱ的第i个元素为1，其余元素均为0. 由式(3)所述的状态转移方程描述了相邻时刻状态向量之间的关系：

需要注意的是，并未限制在每一步随机游走的过程中游走者不能跳回上一步节点，这是为了使状态转移矩阵P能分解为式(2)所示的矩阵运算. 在此基础上添加重启机制，即在每步游走时，有一定可能跳回到初始节点v_i，跳回概率为c(0＜c＜1). 则状态转移方程可调整为：

当随机游走过程进入稳态时，其状态向量保持不变，记π_∞ⁱ为平稳状态向量，此时π_t+1ⁱ=π_tⁱ=π_∞ⁱ，代入式(4)可解得：

因此，可以定义节点对v_i，v_j的平稳解RWR分数：

式(6)将随机游走者从初始节点v_i出发并到达v_j的平稳概率作为节点对的相似性分数，其大小表征了从v_i到v_j的可达性，内在编码了超图的拓扑结构. 很明显，该分数并不具有对称性，即RWR(v_i，v_j)≠RWR(v_j，v_i).

受普通图链路预测方法和已有超图研究的启发，本文设计了一些超图上刻画节点对相似性的方法，以下列举这些基础方法基于节点对输入的定义.

1) 共同邻居指标(Common Neighbors，简称CN). 共同邻居指标是传统链路预测中最简单也是最经典的指标. 该指标基于“共同邻居越多的节点对越相似”这一思想，计算公式为^[13]：

式中N_vi是节点v_i的邻居集合，在超图中，它是指与节点v_i共存于同一超边内的其他所有节点.

2) 共存超边指标(Coexist Edge，简称CE). 不同于普通图，在超图环境中，由于边大小的任意性，两个节点往往会被多个超边同时包含. 统计包含节点对的超边个数便得到共存超边指标，其计算公式为：

式中E_vi是包含节点v_i的超边集合.

3) Jaccard指标(简称JC). Jaccard指标^[14]最初用来计算两集合之间的相似性. 在超图中，用该指标计算节点对之间的相似性定义如下：

4) Adamic-Adar指标(简称AA). Adamic-Adar指标^[15]在CN的基础上考虑了共同邻居的权重，权重是共同邻居的邻居数对数的倒数. 在超图中，对于节点，可以将共存于同一超边的其他节点看作“点邻居”，将节点所关联的超边看作“边邻居”. 对于超边，可以将所包含的节点看作点邻居，将具有共同关联节点(即相交)的超边看作边邻居. 由于邻居可分为点邻居和边邻居，点邻居、边邻居的不同组合对应4种不同的AA指标，分别为VV_AA、VE_AA、EV_AA、EE_AA. 计算公式如下：

指标名称的第一个和第二个字母分别代表共同邻居和共同邻居的邻居的性质. 例如，VE_AA表示节点对的共同邻居为“点邻居”，而共同邻居的邻居为“边邻居”，也即计算与节点对均为邻居的节点权重，权重由该邻居所关联的超边数量计算所得. k_vV(z)、k_vE(z)统计了节点z的邻居节点个数和关联超边个数，而k_eV(z)、k_eE(z)则统计了超边z所包含的节点个数及超边z所相交的超边个数，一般将k_vE和k_eV看作节点和超边的度^[16].

5) α阶局部游走指标. α阶局部游走指标定义在游走的基础之上，将节点对之间α阶游走的数量作为分数. 在普通图中，形如v_i0，v_i1，…，v_iα-1这样，节点个数为α且相邻节点在图中互为邻居的节点序列被称之为一次α阶游走. 扩展到超图上^[17]，超图上的一次α阶游走可定义为一个节点、超边交替出现的序列：

其长度等于α，即超边出现的次数. 同样，序列中的相邻元素在对应超图中相互关联. 节点对之间的α阶游走数量，即α阶局部游走指标可表示为：

上述所提及方法均只计算了超图内节点对的相似性，现在将其适用范围扩展至节点组. 给定超链路预测方法f及超图H=〈V，E〉，对于节点对v_i，v_j∈V，其输出分数为f_H(v_i，v_j)，记节点组ẽ∈2^V\V，则对应的超链路预测分数由式(13)给出：

该式首先计算了每个节点对的连接强度，并将所有节点对的连接强度的算术平均值作为边缘密度. 例如，ẽ的RWR分数可计算为：

在社交领域，式(14)所蕴含的思想直观且有效：若一组成员之间两两关系亲密，那么他们更有可能组成一个团体.

本文引入了9个真实超图，其领域覆盖了食谱、生物、合作、社交等方面. 各数据集的详细统计信息见表 1. 表 1由真实数据构建的超图拓扑结构性质，其中n，m，〈k_vE〉，〈k_vV〉，〈|e|〉，d(H)，|E₂|，|E₃|，|E₄|，|E₅|，分别表示超图的节点数，超边数，节点超度的平均值，节点一阶邻居数的平均值，超边大小的平均值，密度^[18]，超边大小分别为2，3，4，5的超边数量.

1) chuancai^[1]：菜谱数据集，节点由食材构成，一道川菜所需的一组食材构成一条超边.

2) iAB_RBC_283，iJO1366^[1]：人类、大肠杆菌代谢反应数据集. 超边表示生物体内的代谢反应，边内的节点表示参与该反应的反应物.

3) CoreComplex：本文构建了人类蛋白质相互作用数据集. 超边代表人体内的蛋白质相互作用，其包含的节点表示参与相互作用的蛋白质.

4) Cora-Co-citation，Cora-Co-reference^[19]：这两个是引文数据集，两者的节点均表示机器学习论文. 在Cora-Co-citation超图中，超边连接了被同一篇论文所引用的所有论文. 而在Cora-Co-reference中，引用了同一篇论文的论文组成一条超边.

5) DBLP-Co-authorship^[20]：这是一个计算机领域的论文合作数据集. 节点表示论文作者，超边连接了同一篇文章的所有作者.

6) cat-edge-music-blues-reviews^[21]：这是一个共评论数据集. 节点是亚马逊购物网上的用户，在一个月内评论过相同布鲁斯音乐产品的用户组成一条超边.

7) email-Eu^{[6, 22-23]}：线上社交数据集. 节点表示欧洲科研机构的电子邮箱，超边是一次邮件发送，由邮件发送者和所有接收者所组成. 原始数据集中，email-Eu图的超边带有时间戳，这里将多个带时间戳的超边合并成一个超边以静态化原始数据集.

如何验证第2章所列举的链路预测方法在超图环境下的有效性，即指标f是否有能力将有潜力形成超边的节点组和普通节点组区分开来. 一个自然的想法是：随机选取一条超边，同时从超图节点集中随机选取一个相同大小且无重复元素的节点组，前者的f指标分数大于后者的概率越大，指标f就有效.

基于上述想法，分别对所扩展的CN、CE和WK₂方法进行抽样分析. 具体来说，对于任意一个真实图H=〈V，E〉，首先将2^V\V内(不考虑大小为1的超边)所有节点组分为两大类：超边节点组和任意节点组. 顾名思义，一个超边节点组e∈E，其本身构成了一条超边. 而任意节点组ẽ∈2^V\V取自超图所有可能的超边集合. 利用抽样算法分别得到超图的超边节点组和任意节点组的分数样本集合，并利用这些样本生成超边节点组和任意节点组在超图上的指标分数分布，最后比较两组分布和统计特征的差异性. 考虑到超图上的高阶特性，进一步细化抽样工作：抽样算法1以节点组大小为区分分开进行抽样，从而可生成不同大小节点组的分数分布. 注意到在对超边节点组进行抽样时，算法1首先将该节点组形成的超边所移除以模拟该超边形成前的环境.

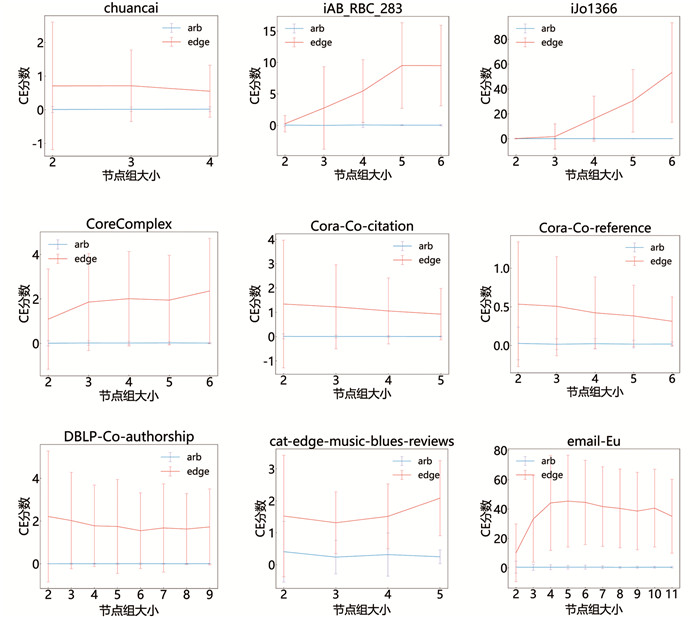
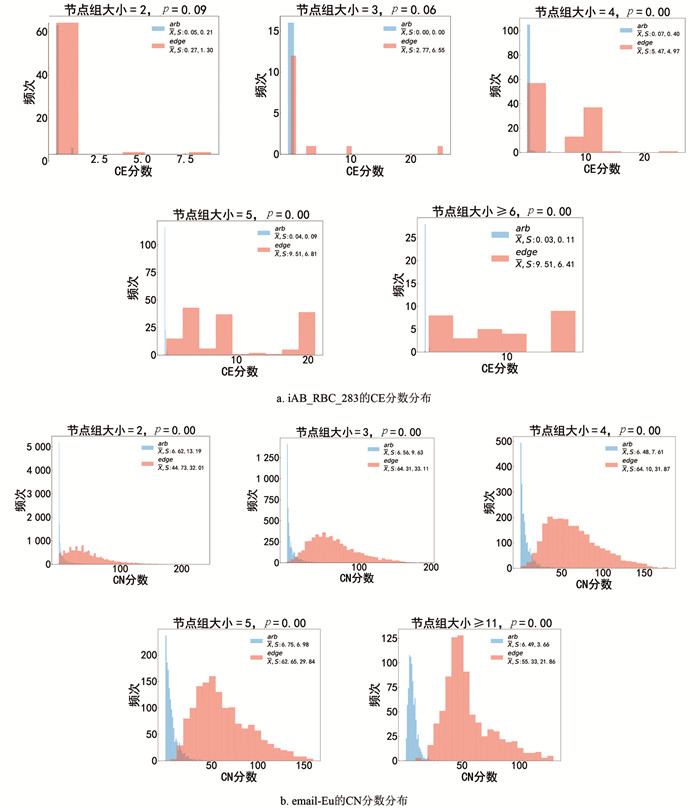
由于空间有限，图 1仅展示部分数据集的部分方法分数分布，还展示了分布的样本均值X、样本标准差S以及两节点组分布t检验的p值. 由于各数据集中超边数量总体呈“小超边多、大超边少”的幂律分布趋势，在生成分数分布时，对小尺寸的节点组单独进行统计，而对大尺寸节点组进行联合统计. 同时绘制了各分数分布的误差棒图，图 2进行了部分展示. 实验结果表明CN及其衍生方法(VVAA、VEAA)、CE及其衍生方法(EVAA，EEAA，JC)、WK₂和WK₃的分布形状较为类似，其差别在于取值范围及精度，以下着重分析可解释性较强的CN、CE和WK方法的分数分布.

各数据集任意节点组的分数分布都极其类似，其分数严重集中在低分值，且均值方差几乎没有变化，本文将其作为对照组来观察同尺寸的超边节点组分数分布. 在生物代谢图上，超边节点组所有分数抽样分布的变化都十分统一：开始时节点组的分数基本集中于低分值上，随着节点数的增加，其样本分数的取值范围逐渐增大且更加均匀地分布于各个区间. 观察iAB_RBC_283的CE分数分布(图 1a)，该数据集的节点组CE分数表示节点组内各反应物平均共同参与的反应数. 可以看到，2，3-超边节点组的分数并未显著大于同尺寸任意节点组(p＞0.05)，而4-超边节点组相当一部分超边节点组的分数落在了10左右，当节点组大小为5时，超边节点组的分数更均匀地落在了大分数上，这表明多反应物的代谢反应显著依赖于反应物两两之间的可反应程度，且依赖程度随代谢反应规模的增加而增加. 蛋白质代谢图CoreComplex的各分数分布也有类似变化，但并未表现得像前两者显著.

cat-edge-music-blues-reviews和DBLP-Co-authorship图的超边分别以“兴趣”和“合作”关系将代表各用户的相关节点相连. 这两个图的构成具有一定的相似性，即由代表人的节点因为共同事件所联系到一起，CE、CN分别表征了人们之间共同参与事件及共同参与者的数量. 而两者超边节点组分数分布也比较类似. 以cat-edge-music-blues-reviews图为例，超边节点组在CN与CE上的分数分布表明：节点组增大时，虽然人们之间共同购买的产品并未显著变化，但用CN所统计的用户的共同兴趣者却大大增加. 对于邮件收发图email-Eu，除2-超边节点组外，email-Eu图各方法分数分布在其余大小的节点组上几乎没有差别，即均表现为均值类似的正态分布(图 1b). 且各方法分数分布的均值总体先上升后保持平稳(略有上升或下降)，造成这种现象的一个解释是“朋友在工作中产生”，工作环境下的多次群发促成了日后代表亲密关系的“一对一沟通”.

总体上看，由于超边形成机理相同，同一领域数据集的超边节点组分数分布相似. 而不同数据集超边节点组的各方法分数抽样分布与均值方差变化呈现两种趋势，要么没有明显变化，要么初始时显著上升. 这说明两点：第一，各方法以多视角衡量了节点组之间节点对的亲密程度. 第二，超图的“派系闭合假说”认为，大关系在形成前，其内部节点之间的联系已经非常紧密. 基于此，演化良好的超图，大尺度超边节点组内部节点对的亲密程度必然大于2-超边节点组. 如若不然，超边节点组内的各个亲密节点对更倾向于生成各种细密的2-超边而没有继续扩张的趋势. 甚至于在大部分数据集中，2-超边节点组和2-任意节点组之间分数分布几乎没有差异. 一般认为，方法对超边节点组和任意节点组的评分差异越大，该方法预测能力越强. 上述情况会使得各方法很难将大小为2的超边节点组和其他节点组区分开来从而导致误判. 例如，两个引文图Cora-Co-citation和Cora-Co-reference的所有方法的超边节点组分数抽样分布几乎不受节点组大小的影响，由于没有明显的演化规律和超边节点组与任意节点组之间的分数差异不明显，所提出的方法对这两个图的链路预测效果将不会太理想. 总的来说，通过抽样及之后的分析，在验证了已抽样方法的有效性——即它们的确能区分正负样本的同时，还发现在大多数情况下，这种区分能力和节点组的大小有关，即对大尺寸节点组的区分能力要远远强于小尺寸节点组. 由于真实超图的超边大小分布往往展现为幂律，即小尺寸超边占绝大多数，因此，对小尺寸、甚至于2-节点组的无力是制约超链路预测方法性能的主要桎梏.

本文使用经典的二分类全局指标——接收者操作特征曲线下面积(AUC)，与局部指标——精确率(precision@k)和召回率(recall@k)，来评估第2节所列举方法在各真实图上的表现. 对单个数据集及特定指标的每次实验，采用五折交叉验证的方式进行并重复若干次，记录每次实验的交叉验证平均值. 参数设置上，RWR的游走重启概率c固定为0.15.

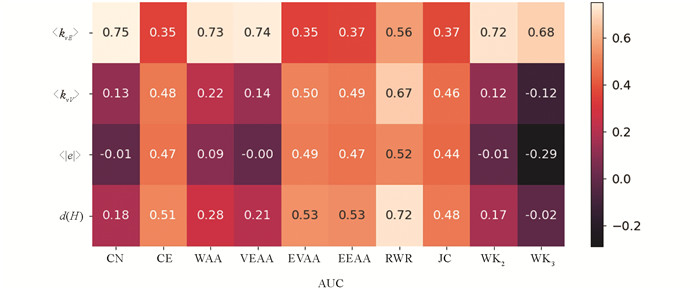
预测结果的AUC评价展示在表 2，可以看到，并未有任何一种方法在所有数据集上表现得最好，这便是超链路预测环境下的“天下没有午餐定律”^[24]. 令人惊喜的莫过于CE，该方法定义十分简单，却在iAB_RBC_283、iJO1366、CoreComplex、Cora-Co-reference、DBLP-Co-authorship上表现优异. 将CE应用于这些数据集还能得到更加直观的物理解释，例如，对于合作图DBLP-Co-authorship，以CE方法的视角来看，当一群作者相互之间合作过很多次时，他们更有可能组团进行合作. 在数据集chuancai和email-Eu上，CN方法有着不错的性能表现. 以email-Eu为例，CE方法计算了节点组内节点对之间的平均邮件收发事件数，而CN方法计算了各自参与的邮件收发事件的其他共同参与者数量，这表明，有着更多工作伙伴关系的成员组之间更有可能产生邮件收发事件. 在普通图的链路预测中，奇数步局部游走指标在代谢图上效果良好^[25]，如果将CE看作“WK₁”，其效果在生物数据集上表现最优也就不足为奇了. JC作为CE的加权，整体上前者的表现不如后者，这也说明了链路预测方法的准确度并非与其计算复杂度呈正比. 对于在超图环境中所扩展的4类AA方法，若分别将VVAA、VEAA看作CN的改进，EVAA、EEAA看作CE的改进，则这两组方法内部之间的性能表现都十分接近. 且将点邻居个数看作共同邻居或共存超边的权重时(VV_AA之于CN、EV_AA之于CE)，整体有着更为明显的性能提升，这可能是由于点邻居的数量相对于边邻居更多，致使其权重的粒度更加细致从而有着很好的区分度. RWR在各数据集上的AUC表现似乎与邻域方法、特别是CE的表现正相反，如前者在chuancai、cat-edge-music-blues-reviews、email-Eu上具有较优秀的预测效果，而后者在除这些以外的其他数据集上有着较好的表现，这表明在超链路预测任务中，节点间的全局特征与局部特征都能提供有效信息. 同时本文对某一方法作用于所有数据集上的链路预测性能(AUC分数)与所有数据集的某一特定统计特征进行了相关性计算，热力图见图 3. 总体上看，超图的“规模”越大，其可预测性越好，注意到〈k_vE〉，即所谓超图的平均超度^[26]与方法的预测性能之间呈显著正相关，这意味着该指标的大小直接展示了数据集可利用信息的多少.

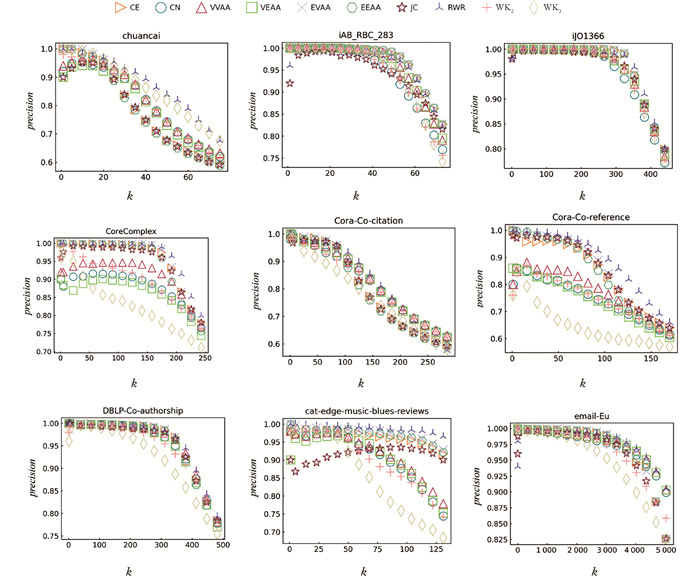
预测结果的精确率及召回率曲线分别展示在图 4、图 5，两者的阈值上限取各数据集测试集样本数量的一半. 不同于在AUC表现上的“百家争鸣”，精确率及召回率曲线上扩展的RWR方法在所有数据集上均取得了不错的效果，说明所引入超图随机游走方式的有效性，即该过程确实能够捕捉到超图的拓扑结构. 局部游走指标(WK₂、WK₃)效果普遍较差，两者的效果随着阈值k的增加而快速下降，这可能是因为在扩展局部游走时并未考虑“游走宽度”^[17]，从而丢失了超边的“高阶特性”. 总的来说，各方法虽然在性能上有所差异，但正如本章第2节所言，所扩展的方法在应用于超链路环境中时，都能够对正负样本有效地进行预测.

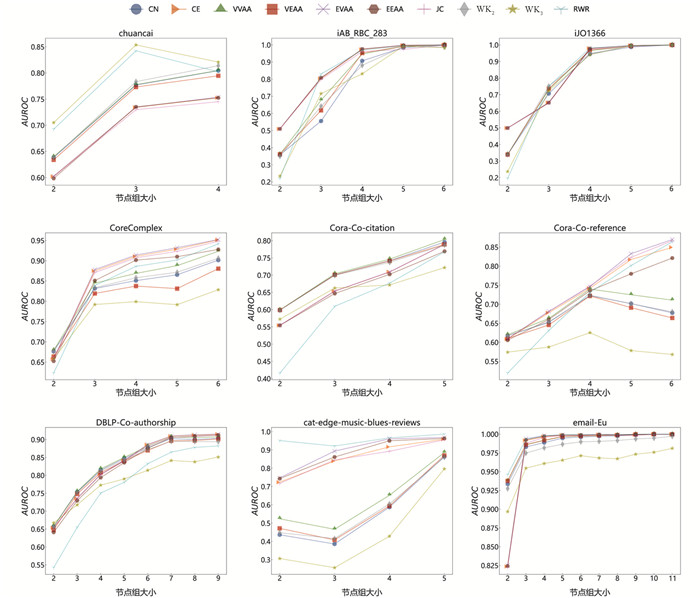
延续抽样时的方式，在链路预测完成后，对各方法应用于各数据集的表现分节点组大小进行评估，评估结果见图 6. 与抽样类似的是，各方法2-节点组上的链路预测效果明显低于其他节点组. 例如，对于iAB_RBC_283，2-超边节点组的CE、CN分数分布并未显著大于任意节点组，相对应，很多方法对该数据集2-节点组进行链路预测的AUC效果甚至低于0.5. 对于大尺寸节点组，各方法在整体上表现一致. 这一现象不仅与抽样结果相吻合，还从链路预测角度体现了大超边内部节点的强链接程度. 与抽样不同的是，AUC的效果评估曲线在绝大部分数据集上呈现绝对递增的趋势，即随着节点组节点数的增加，各方法在数据集上的链路预测效果越来越好.

本文给出了将链路预测方法扩展到超图环境的一般方式，并基于此方式扩展了11种方法. 对所扩展的方法在真实超图上进行分数抽样并生成了对应的分数抽样分布，验证了扩展方法的有效性，发现了不同数据集的超边演化规律，认为演化良好的超图其超边内部的联系强度随节点数增加而增加，由此推论超链接预测的主要难点在于对小尺寸超边的预测. 然后，将所扩展方法直接应用于真实超图的超链路预测，链路预测结果表明，不同方法适用于不同的超图环境，但在局部精确率和召回率上，RWR有着更好的性能. 还根据节点组大小对预测效果分别进行评估，结果表明在同一数据集内，扩展方法的性能随着节点组节点数的增加而增加.

在未来的研究中，希望引入除式(13)外更多的扩展方式以达到性能的进一步提升. 对于具体的链路预测方法，在普通链路预测指标的基础上，希望加入更多超图独有的高阶性质，如“宽度”^[17]、“高阶随机游走”^[27]等，另外，更希望所设计的方法能有效地应对当前方法在预测小尺寸超边上的无力. 最后，关于超边下采样算法的讨论正如火如荼^{[2, 28-29]}，期待在未来，使用最新的下采样算法所得到更加“仿真”的负样本能更好地评估方法的性能.