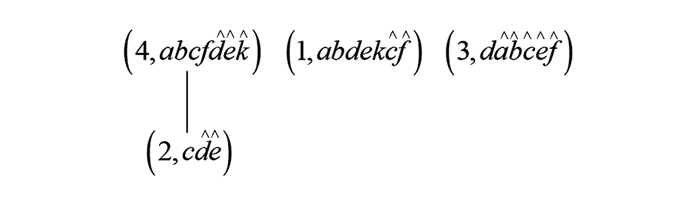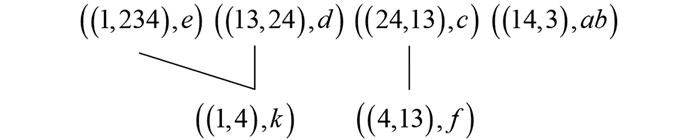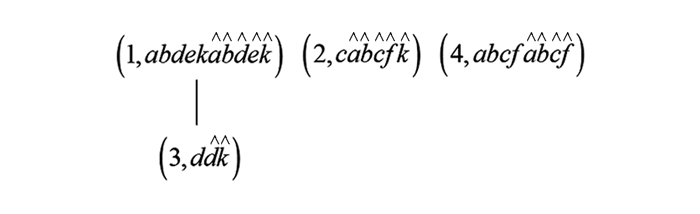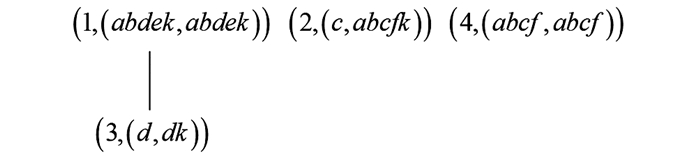本节主要介绍形式背景、直观图和不完备背景的基础知识以及集合幂集的笛卡尔积上的相关运算.

定义1^[1]  称$K=(G, M, I)$为一个形式背景, 其中, $G=\left\{g_{1}, g_{2}, \cdots, g_{p}\right\}$为对象集, 每个$g_{i}(i \leqslant p)$称为一个对象; $M=\left\{m_{1}, m_{2}, \cdots, m_{q}\right\}$为属性集，每个$m_{j}(j \leqslant q)$称为一个属性; $I$为$G$和$M$之间的二元关系, $I \subseteq G \times M$. 若$(g, m) \in I$, 则称对象$g$具有属性$m$; 若$(g, m) \notin I$, 则称对象$g$不具有属性$m$.

注1  本文所研究的形式背景是有限的且是正则的.

定义2^{[1, 8]}  设$K=(G, M, I)$为形式背景. 对于对象子集$X \subseteq G$, 属性子集$A \subseteq M$, 定义

*算子：

*算子：

记$I^{c}=(G \times M) \backslash I$, 则称$K^{c}=\left(G, M, I^{c}\right)$为$K=(G, M, I)$的补背景. 事实上, $\bar{*}$算子就是$K^{c}$上的* 算子.

定义3^[1]  设$K=(G, M, I)$为形式背景. 对于任意的$X \subseteq G, A \subseteq M$, 若$X=A^{*}$且$A=X^{*}$, 则称$(X, A)$是一个形式概念, 简称概念. 其中, $X$为概念的外延, $A$为其内涵. 记所有概念的集合为$L(K)$.

定理1^[1]  设$K=(G, M, I)$为形式背景. 若对于任意$\left(X_{1}, A_{1}\right), \left(X_{2}, A_{2}\right) \in L(K)$, 定义如下偏序关系和上、下确界，

则L(K)是完备格，称为概念格.

对于给定的一个形式背景，文献[23]提出了对象直观图和属性直观图的定义，并基于此研究了概念的获取方法. 相关的定义和方法如下：

定义4^[23]  设K=(G，M，I)是形式背景. 记

对任意的g_i，g_j∈G，若g_i^*$\subseteq$g_j^*，则记

称$\left(H_{G}^{*}(K), \leqslant\right)$是形式背景$K$的对象直观图. 对偶的, 对任意的$m_{s}, m_{t} \in M$, 若$m_{s}^{*} \subseteq m_{t}^{*}$, 则记

称$\left(H_{M}^{*}(K), \leqslant\right)$是形式背景$K$的属性直观图.

注2  在定义4中, $[g]$表示对象$g$的等价类, $[m]$表示属性$m$的等价类.

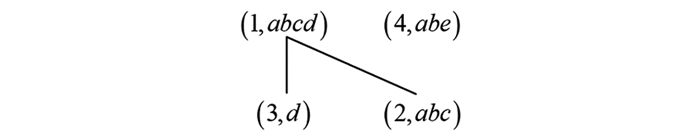
例1  表 1为形式背景$K=(G, M, I)$, 其对象直观图和属性直观图分别如图 1和图 2所示.

通过直观图获取概念的方法如下：

定理2^[23]  设K=(G，M，I)是形式背景，(H_G^*(K)，≤)和(H_M^*(K)，≤)分别是其对象直观图和属性直观图. 则以下结论成立：

1) $\forall\left([g], g^{*}\right) \in H_{G}^{*}(K)$, 有

2) $\forall\left(m^{*}, [m]\right) \in H_{M}^{*}(K)$，有

其中

$\tau$和$\omega$为指标集.

定理2表明，我们可以通过形式背景的直观图得到一些概念. 由于这些概念包含了概念格中的交、并不可约元，因此通过概念格中的上、下确界运算进一步可以得到所有的概念^[23].

定义5^[17]  称四元组$I K=(G, M, \{+, ?, -\}, J)$为不完备背景. 其中: $G$为对象集; $M$为属性集; $\{+, ?, -\}$为属性值集; $J: G \times M \longrightarrow\{+, ?, -\}$为映射. 若$J(g, m)=+$, 则表示对象$g$拥有属性$m$; 若$J(g, m)=?$, 则表示不确定对象$g$是否拥有属性$m$; 若$J(g, m)=-$, 则表示对象$g$不拥有属性$m$.

称K=(G，M，I)为不完备背景IK=(G，M，{+，?，-}，J)的一个完备化^[18]，此时二元关系I满足条件：

即$I$可以通过将不完备背景中的每个“?”替换为“+”或"-”来获得. 若将不完备背景中的所有“?”替换为“-”, 得到的形式背景称为$I K$的最小完备化, 记为$I K_{-}=\left(G, M, I_{-}\right)$; 若将不完备背景中的所有“?”替换为“+”, 得到的形式背景称为$I K$的最大完备化, 记为$I K_{+}=\left(G, M, I_{+}\right)$.

例2^[22]  表 2为不完备背景IK=(G，M，{+，?，-}，J)，其最小完备化IK_-和最大完备化IK₊分别如表 3和表 4所示.

本小节主要回顾任意非空有限集合幂集的笛卡儿积上的相关运算.

设$S$为任意的非空有限集合，$\mathscr{D} \mathscr{P}(S)=\mathscr{P} S) \times \mathscr{P}(S)$是$S$幂集的笛卡儿积，对任意的$(A, B), (C, D) \in$ $\mathscr{D} \mathscr{P}(S)$, 定义偏序关系及交、并、补运算为:

特别地，当(A，B)=(C，D)时，A=C且B=D.

本节基于直观图，从两个角度给出三支近似概念的获取方法. 一是从三支近似概念格与某些特定形式背景概念格的同构关系出发，二是从三支近似算子的角度出发. 下面先给出三支近似概念的相关知识.

定义6^[22]  设$I K=(G, M, \{+, ?, -\}, J)$为不完备背景. 对任意的$X, Y \subseteq G, A, B \subseteq M$, 定义

1) OE三支近似算子：

2) AE三支近似算子：

式中

称*为正算子，*为负算子.

事实上，这里的正算子*是IK最小完备化IK_-中的算子*，而负算子*是IK最大完备化IK₊中的算子*.

定义7^[22]  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景. 对任意的$X, Y \subseteq G, A, B \subseteq M$,

1) 若满足$X^{\lessdot}=(A, B)$且$(A, B)^{\gtrdot}=X$, 则称$(X, (A, B))$为$I K$的对象导出三支近似概念, 简称$O E$近似概念. 其中, 称$X$为$O E$近似概念的外延, $(A, B)$为其内涵.

2) 若满足$(X, Y)^{\gtrdot}=A$且$A^{\lessdot}=(X, Y)$, 则称$((X, Y), A)$为$I K$的属性导出三支近似概念, 简称$A E$近似概念. 其中, 称$(X, Y)$为$A E$近似概念的外延, $A$为其内涵.

用$O E L(I K)$表示$I K$中所有$O E$近似概念的集合, $A E L(I K)$表示$I K$中所有$A E$近似概念的集合.

定理3^[22]  设IK=(G，M，{+，?，-}，J)为不完备背景.

1) 对于任意的两个OE近似概念，定义偏序关系以及上、下确界如下：

则OEL(IK)是完备格，称为对象导出三支近似概念格，简称OE近似概念格.

2) 对于任意的两个AE近似概念，定义偏序关系以及上、下确界，如下：

则AEL(IK)是完备格，称为属性导出三支近似概念格，简称AE近似概念格.

例3^[22](续例2)  对于表 2的不完备背景，其OE近似概念格和AE近似概念格分别如图 3和图 4所示.

本文记最小完备化与最大完备化的补背景的并置为$I K_{-} \mid I K_{+}^{c}=\left(G, M \cup \hat{M}, I_{-} \cup I_{+}^{c}\right)$, 其中$\hat{M}=$ $\left\{\hat{m}_{j} \mid m_{j} \in M\right\}$, 对应的概念格记为$L\left(I K_{-} \mid I K_{+}^{c}\right)$; 记最小完备化与最大完备化的补背景的叠置为$\frac{I K_{-}}{I K_{+}^{c}}=$ $\left(\hat{G} \cup G, M, I_{-} \cup I_{+}^{c}\right)$, 其中$\hat{G}=\left\{\hat{g}_{i} \mid g_{i} \in G\right\}$, 对应的概念格为$L\left(\frac{I K_{-}}{I K_{+}^{c}}\right)$.

注3  为了便于后续内容的描述，本文将两个形式背景并置所构成的新形式背景称为并置背景，将它们叠置所构成的新形式背景称为叠置背景.

对于OE近似概念和AE近似概念，文献[22]给出了通过不完备背景的最小完备化和最大完备化的补背景的并置和叠置获取这两种三支近似概念的方法，具体内容如下.

定理4^[22]  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $I K_{-} \mid I K_{+}^{c}$和$\frac{I K_{-}}{I K_{+}^{c}}$分别是$I K$的最小完备化和最大完备化的补背景的并置背景和叠置背景, 则有

1) 存在一个同构映射f₁：

有$f_{1}((X, (A, B)))=(X, A \cup \hat{B})$, 其中$\hat{B}=\{\hat{b} \mid b \in B\}$.

2) 存在一个同构映射f₂：

有$f_{2}(((X, Y), A))=(X \cup \hat{Y}, A)$, 其中$\hat{Y}=\{\hat{y} \mid y \in Y\}$.

定义8^[24]  对任意的$(P, Q) \in \mathscr{P}(G) \times \mathscr{P}(M \cup \hat{M})$，定义

称[·]_m为属性分离映射，其中

类似地, 对任意的$(P, Q) \in \mathscr{P}(G \cup \hat{G}) \times \mathscr{P}(M)$, 定义

称$[\cdot]_{g}$为对象分离映射, 其中$P_{1}=\{g \mid g \in P \cap G\}, P_{2}=\{g \mid \hat{g} \in P \cap \hat{G}\}$.

通过定理2可从$\left(H_{G}^{*}(K), \leqslant\right)$和$\left(H_{M}^{*}(K), \leqslant\right)$中获取概念, 于是结合定理4的1$)$和定义8中的式(3), 可得从$\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$和$\left(H_{M}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$中直接获取不完备背景中$O E$近似概念的方法.

定理5  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$和$\left(H_{M}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$分别是并置背景$I K_{-} \mid I K_{+}^{c}$的对象直观图和属性直观图. 则下列结论成立:

1) $\forall\left([g], g^{*}\right) \in H_{G}^{*}\left(I K_{-} \mid I K_{+}^{c}\right)$, 有

2) $\forall\left(m^{*}, [m]\right) \in H_{M}^{*}\left(I K_{-} \mid I K_{+}^{c}\right)$, 有

定理5表明，对于不完备背景，我们可以通过并置背景IK_-|IK₊^c的对象直观图或属性直观图得到部分的OE近似概念. 而通过对这些部分的OE近似概念进行上确界或下确界运算，便可以得到所有的OE近似概念. 下面我们以对象直观图为例，给出具体的求解步骤.

1) 画出并置背景IK_-|IK₊^c的对象直观图(H_G^*(IK_-|IK₊^c)，≤).

2) 对$\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$中的元素, 先根据定理2中的式(1) 进行运算$\lambda_{\cap}{ }^{\circ} \uparrow$, 再根据定义8中的式(3) 进行运算$[\cdot]_{m}$.

3) 对步骤2)得到的OE近似概念，根据定理3的1)进行上确界运算便可得其他的OE近似概念.

例4(续例2)  最小完备化IK_-和最大完备化IK₊的补背景的并置背景IK_-|IK₊^c如表 5所示.

根据定义4，可得

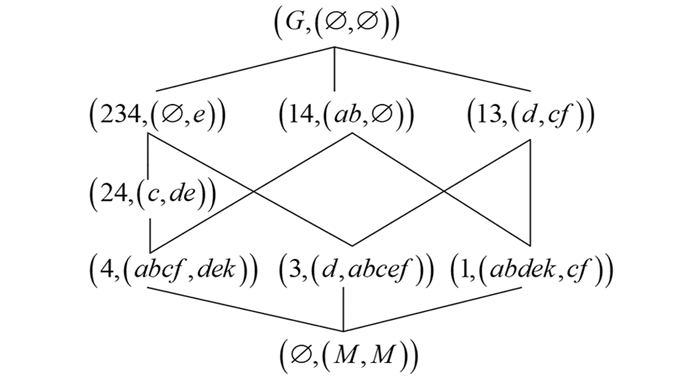
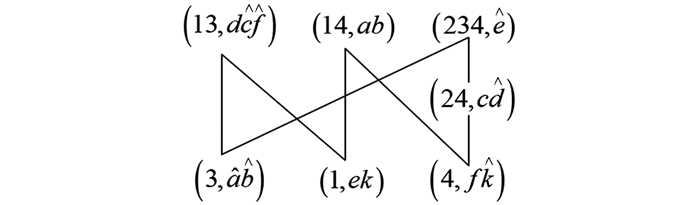
进而可得并置背景的对象直观图和属性直观图分别如图 5和图 6所示.

对于对象直观图$\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$中的元素$(2, c \hat{d} \hat{e})$, 根据定理2中的式(1) 的运算$\lambda_{\cap}{ }^{\circ} \uparrow$可得

再由定义8中的式$(3)$可得

对于属性直观图$\left(H_{M}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$中的元素$(24, c \hat{d})$, 根据定理2中的式(2) 的运算$\mu_{\cap }^{}{\circ} \uparrow$可得

再由定义8中的式(3)可得

由图 3分别可以验证$\left[\lambda_{\cap}(\uparrow(2, c \hat{d} \hat{e}))\right]_{m} \in O E L(I K)$和$\left[\mu_{\cap}(\uparrow(24, c \hat{d}))\right]_{m} \in O E L(I K)$.

下面通过结合定理2和定理4的2$)$, 可得从$\left(H_{G}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$和$\left(H_{M}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$中直接获取不完备背景中$A E$近似概念的方法.

定理6  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $\left(H_{G}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$和$\left(H_{M}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$分别是叠置背景$\frac{I K_{-}}{I K_{+}^{c}}$的对象直观图和属性直观图. 则下列结论成立:

1) $\forall\left([g], g^{*}\right) \in H_{G}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right)$, 有

2) $\forall\left(m^{*}, [m]\right) \in H_{M}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right)$, 有

定理6表明，我们可以通过叠置背景$\frac{I K_{-}}{I K_{+}^{c}}$的对象直观图或属性直观图得到部分的AE近似概念. 类似地，通过对这些AE近似概念进行上确界或下确界运算，便可以得到所有的AE近似概念. 下面我们仍以对象直观图为例，给出具体的求解步骤.

1）画出叠置背景$\frac{I K_{-}}{I K_{+}^{c}}$的对象直观图$\left(H_{G}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$.

2) 对$\left(H_{G}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$中的元素, 先根据定理2中的式(1) 进行运算$\lambda_{\cap}{ }^{\circ} \uparrow$, 再根据定义8中的式(4)进行运算$[\cdot]_{g}$.

3) 对步骤2)得到的AE近似概念，根据定理3的2)进行上确界运算便可得其他的AE近似概念.

例5(续例2)  最小完备化IK_-和最大完备化IK₊的补背景的叠置背景$\frac{I K_{-}}{I K_{+}^{c}}$如表 6所示.

根据定义4，可得

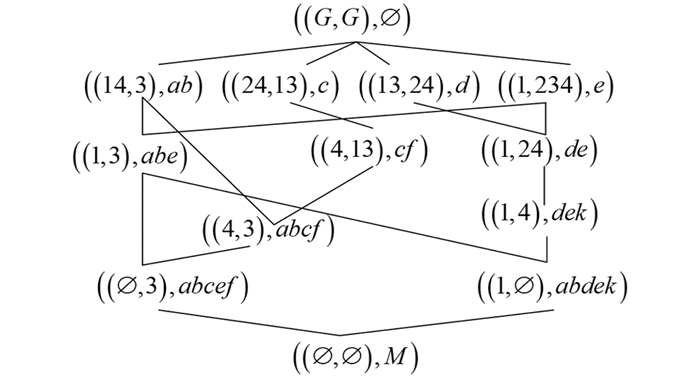
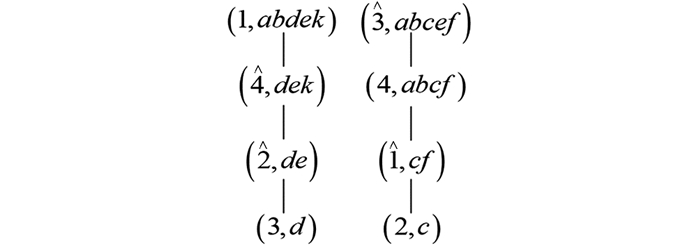
进而可得叠置背景的对象直观图和属性直观图分别如图 7和图 8所示.

对于对象直观图$\left(H_{G}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$中的元素$(\hat{2}, d e)$, 先根据定理2中的式(1) 的运算$\lambda_{\cap}^{}{\circ} \uparrow$可得

再由定义8中的式(4) 可得

对于属性直观图$\left(H_{M}^{*}\left(\frac{I K_{-}}{I K_{+}^{c}}\right), \leqslant\right)$中的元素$(4 \hat{1} \hat{3}, f)$, 先根据定理2中的式(2) 的运算$\mu_{\cap}^{}{\circ} \uparrow$可得

再由定义8中的式(4) 可得

由图 4分别可以验证$\left[\lambda_{\cap}(\uparrow(\hat{2}, d e))\right]_{g} \in A E L(I K)$和$\left[\mu_{\cap}(\uparrow(4 \hat{1} \hat{3}, f))\right]_{g} \in A E L(I K)$.

定义9  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景. 记

对任意的$g_{i}, g_{j} \in G$, 若$\left(g_{i}^{*}, g_{i}^{\bar{*}}\right) \subseteq\left(g_{j}^{*}, g_{j}^{\bar{*}}\right)$, 则记

并称$\left(H_{G}^{\lessdot}(I K), \leqslant\right)$是$I K$的对象三支近似直观图. 对偶的, 对任意的$m_{s}, m_{t} \in M$, 若$\left(m_{s}^{*}, m_{s}^{\bar{*}}\right) \subseteq\left(m_{t}^{*}\right.$, $\left.m_{i}^{\bar{*}}\right)$, 则记

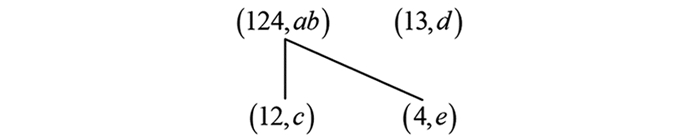
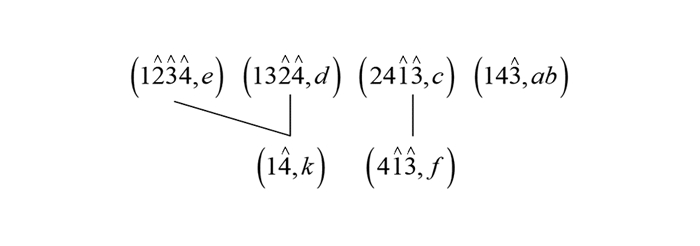
并称$\left(H_{M}^{\lessdot}(I K), \leqslant\right)$是$I K$的属性三支近似直观图.

例6(续例2)  对于表 2所示的不完备背景，其对象三支近似直观图和属性三支近似直观图分别如图 9和图 10所示.

由定义9和定义4易知, 不完备背景$I K$的对象(属性) 三支近似直观图和并置背景$I K_{-} \mid I K_{+}^{c}$(叠置背景$\frac{I K_{-}}{I K_{+}^{c}}$)的对象(属性) 直观图之间存在一一对应关系. 具体见如下推论.

推论1  对任意的$\left([g], g^{*}\right) \in\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}^{c}\right), \leqslant\right)$, 存在$\left([g], \left(g^{*}, g^{\overline{*}}\right)\right) \in\left(H_{G}^{\lessdot}(I K), \leqslant\right)$, 有

推论2  对任意的$\left(m^*, [m]\right) \in\left(H_M^*\left(\frac{I K_{-}}{I K_{+}^c}\right), \leqslant\right)$, 存在$\left(\left(m^*, m^{\bar{*}}\right), [m]\right) \in\left(H_M^{\lessdot}(I K), \leqslant\right)$, 有

根据上述推论1和推论2以及定理5和定理6, 可得下面的结论.

定理7  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $\left(H_G^{\lessdot}(I K), \leqslant\right)$和$\left(H_M^{\lessdot}(I K), \leqslant\right)$分别是$I K$的对象三支近似直观图和属性三支近似直观图. 则下列结论成立:

1) $\forall\left([g], \left(g^{*}, g^{\overline{*}}\right)\right) \in H_{G}^{\lessdot}(I K)$, 有

2) $\forall\left(\left(m^{*}, m^{\overline{*}}\right), [m]\right) \in H_{M}^{\lessdot}(I K)$, 有

式中

$\tau$和$\omega$为指标集.

证  由推论1和推论2, 以及定理5和定理6可证.

定理7表明，对于不完备背景，我们可以通过对象(属性)三支近似直观图得到部分的OE(AE)近似概念. 再根据近似概念的上确界或下确界运算，便可以得到所有的OE近似概念和AE近似概念. 下面我们以对象三支近似直观图为例，给出具体的求解步骤.

1) 画出$I K$的对象三支近似直观图$\left(H_{G}^{\lessdot}(I K), \leqslant\right)$.

2) 对$\left(H_{G}^{\lessdot}(I K), \leqslant\right)$中的元素, 利用定理2中的式(1) 进行运算$\lambda_{\cap}^{}{\circ} \uparrow$.

3) 对步骤2) 得到的$O E$近似概念, 根据定理3的1) 进行上确界运算便可得其他的$O E$近似概念.

例7(续例6)  对于$\left(H_G^{\lessdot}(I K), \leqslant\right) $中的元素$(2, (c, d e))$, 通过定理2中的式(1) 可得

同样的，对于$\left(H_{M}^{\lessdot}(I K), \leqslant\right)$中的元素$((4, 13), f)$, 根据定理2中的式(2) 可得

由图 3和图 4分别可以验证$(24, (c, d e)) \in O E L(I K)$和$((4, 13), c f) \in A E L(I K)$.

采用与第2节相同的研究方式，本节也是从格同构和近似算子两个角度给出近似概念的获取方法. 下面先给出近似概念的相关知识.

设IK=(G，M，{+，?，-}，J)是不完备背景. 对于$X \subseteq G$，定义^[19]

其中$\underline{R}(X)$是$X$中所有对象一定共同具有的属性全体构成的集合，而$\bar{R}(X)$是$X$中所有对象可能共同具有的属性全体构成的集合. 因此, 一定有$\underline{R}(X) \subseteq \bar{R}(X)$. 当$X=\{g\}$, 记$\underline{R}(\{g\})$和$\bar{R}(\{g\})$分别为$\underline{R}(g)$和$\bar{R}(g)$.

注4  $\underline{R}(\cdot)$是最小完备化$I K_{-}$上的* 运算, $\bar{R}(\cdot)$是最大完备化$I K_{+}$上的$*$运算.

定义10^[19]  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景. 对任意的$X \subseteq G, A, B \subseteq M$, 定义两个算子:

定义11^[19]  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景. 对任意的$X \subseteq G, A, B \subseteq M$, 若满足$X^{\square}=(A, B)$且$(A, B)^{\diamond}=X$, 则称$(X, (A, B))$是$I K$的近似概念. 其中, 称$X$为近似概念的外延, $(A$, $B)$为其内涵. 用$L(I K)$表示所有近似概念的集合.

定理8^[19]  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景. 对于任意的两个近似概念, 定义偏序关系以及上、下确界如下:

则$L(I K)$是完备格, 称为不完备背景的近似概念格.

例8 (续例2)  对于表 2的不完备背景, 其近似概念格如图 11所示.

本文记最小完备化与最大完备化的并置为

对应的概念格记为$L\left(I K_{-} \mid I K_{+}\right)$. 为了便于区分, 我们记并置背景$I K_{-} \mid I K_{+}$上的$*$运算为$\uparrow$. 下面给出并置背景中的算子$\uparrow$与文献[19]中算子$\square, \diamond$的关系.

引理1  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $I K_{-} \mid I K_{+}$是最小完备化与最大完备化的并置背景. 则有

1) 任意的$X \subseteq G, X^{\uparrow}=\underline{R}(X) \cup \hat{\bar{R}(X)}$;

2）任意的$F \subseteq M \cup \hat{M}, F^{\wedge}=(A, B)^{\diamond}$, 其中$A=F \cap M, B=\{b \mid \hat{b} \in F \cap \hat{M}\}$.

证  1) 易由$\underline{R}(X)$和$\bar{R}(X)$的定义及$I K_{-} \mid I K_{+}$的定义可证.

2) 记$\hat{B}=F \cap \hat{M}$, 则$F=A \cup \hat{B}$, 进而由算子$*$的性质$\forall A_{1}, A_{2} \subseteq M, \left(A_{1} \cup A_{2}\right)^{*}=A_{1}^{*} \cap A_{2}^{*}$^[1]可得

因$A \subseteq M, \hat{B} \subseteq \hat{M}$, 故根据$\underline{R}(\cdot), \bar{R}(\cdot)$和$\diamond$的定义可得

下面给出不完备背景的近似概念格与特定形式背景的概念格的同构关系.

定理9  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $I K_{-} \mid I K_{+}$是$I K$的最小完备化和最大完备化的并置背景. 则存在一个同构映射$f_{3}: L(I K) \longrightarrow L\left(I K_{-} \mid I K_{+}\right)$, 有$f_{3}((X, (A, B)))=$ $(X, A \cup \hat{B})$.

证  首先证$(X, A \cup B) \in L\left(I K_{-} \mid I K_{+}\right)$, 即证$f_{3}$是一个映射. 若$(X, (A, B)) \in L(I K)$, 则有

即

以及

进而由引理1可知

因此, 根据定义3可知$(X, A \cup \hat{B}) \in L\left(I K_{-} \mid I K_{+}\right)$. 也就是说$f_{3}$是一个映射.

其次, 证明$f_{3}$是一个双射. 对任意的$(X, F) \in L\left(I K_{-} \mid I K_{+}\right)$, 有$X^{\wedge}=F$且$F^{\uparrow}=X$. 记$A=F \cap$ $M, \hat{B}=F \cap \hat{M}$. 于是有$A=X^{\uparrow} \cap M, \hat{B}=X^{\uparrow} \cap \hat{M}$. 根据引理1可得

即$B=\bar{R}(X)$. 于是, 由算子$\square$的定义可得$X^{\square}=(A, B)$. 又由$X=F^{\uparrow}=(A \cup \hat{B})^{\uparrow}$及引理1可得$X=$ $(A, B)^{\diamond}$. 因此, 可以证得$(X, (A, B)) \in L(I K)$, 即$f_{3}$是一个满射.

对于两个近似概念$\left(X_{1}, \left(A_{1}, B_{1}\right)\right)$和$\left(X_{2}, \left(A_{2}, B_{2}\right)\right)$, 若$\left(X_{1}, \left(A_{1}, B_{1}\right)\right) \neq\left(X_{2}, \left(A_{2}, B_{2}\right)\right)$, 则有$X_{1} \neq X_{2}$；另一方面，

于是

即$f_{3}$是一个单射. 综上可得, $f_{3}$是一个双射.

通过结合定理9和定义8, 可得从$\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}\right), \leqslant\right)$和$\left(H_{M}^{*}\left(I K_{-} \mid I K_{+}\right), \leqslant\right)$中直接获取不完备背景中近似概念的方法如下.

定理10  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}\right), \leqslant\right)$和$\left(H_{M}^{*}\left(I K_{-} \mid\right.\right.$ $\left.\left.I K_{+}\right), \leqslant\right)$分别是并置背景$I K_{-} \mid I K_{+}$的对象直观图和属性直观图，则下列结论成立:

1) $\forall\left([g], g^{*}\right) \in H_{G}^{*}\left(I K_{-} \mid I K_{+}\right)$, 有$\left[\lambda_{\cap}\left(\uparrow\left([g], g^{*}\right)\right)\right]_{m} \in L(I K)$,

2) $\forall\left(m^{*}, [m]\right) \in H_{M}^{*}\left(I K_{-} \mid I K_{+}\right)$, 有$\left[\mu_{\cap}\left(\uparrow\left(m^{*}, [m]\right)\right)\right]_{m} \in L(I K)$.

根据定理10，我们可以通过并置背景IK_-|IK₊的对象直观图或属性直观图得到部分的近似概念. 进而再根据近似概念的上确界或下确界运算，便可以得到所有的近似概念. 下面我们以对象直观图为例，给出具体的求解步骤.

1) 画出IK_-|IK₊的对象直观图(H_G^*(IK_-|IK₊)，≤).

2) 对$\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}\right), \leqslant\right)$中的元素, 先利用定理2中的式(1) 进行运算$\lambda_{\cap}^{}{\circ} \uparrow$, 再根据定义8中的式(3)进行运算$[\cdot]_{m}$.

3) 对步骤2)得到的近似概念，根据定理8进行上确界运算便可得其他的近似概念.

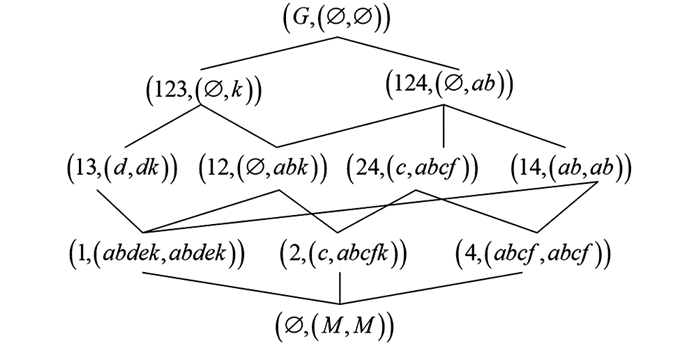
例9(续例2)  最小完备化IK_-和最大完备化IK₊的并置背景IK_-|IK₊如表 7所示.

根据定义4，可得

进而可得并置背景的对象直观图和属性直观图分别如图 12和图 13所示.

对于对象直观图$\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}\right)\right.$) $\left.\leqslant\right)$中的元素$(3, d \hat{d} \hat{k})$, 先根据定理2中的式(1) 的运算$\lambda_{\cap}^{}{\circ} \uparrow$可得

再由定义8中的式(3) 可得

对于属性直观图$\left(H_{M}^{*}\left(I K_{-} \mid I K_{+}\right), \leqslant\right)$中的元素$(24, c \hat{c} \hat{f})$, 先根据定理2中的式(2) 的运算$\mu_{\cap}^{}{\circ} \uparrow$可得

再由定义8中的式(3)可得

由图 11可以分别验证$(13, (d, d k)) \in L(I K)$和$(24, (c, a b c f)) \in L(I K)$.

定义12  设IK=(G，M，{+，?，-}，J)是不完备背景. 记

对任意的$g_{i}, g_{j} \in G$, 若

则记

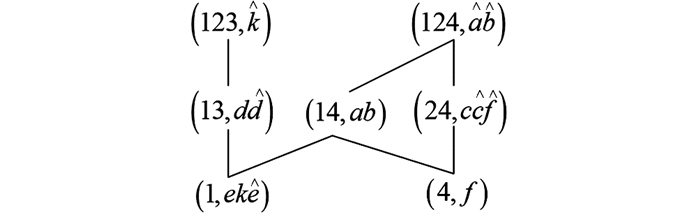
并称$\left(H_{G}^{\square}(I K), \leqslant\right)$是$I K$的对象近似直观图.

例10(续例2)  表 2所示不完备背景的对象近似直观图如图 14所示.

根据定义12和定义4可知，不完备背景IK的对象近似直观图和并置背景IK_-|IK₊的对象直观图之间也存在如下的一一对应关系.

推论3  对任意的$\left([g], g^{*}\right) \in\left(H_{G}^{*}\left(I K_{-} \mid I K_{+}\right), \leqslant\right)$, 存在$([g], (\underline{R}(g), \bar{R}(g))) \in$ $\left(H_{G}^{\square}(I K), \leqslant\right)$, 有

定理11  设$I K=(G, M, \{+, ?, -\}, J)$是不完备背景, $\left(H_{G}^{\square}(I K), \leqslant\right)$是$I K$的对象近似直观图. 则对任意的$([g], (\underline{R}(g), \bar{R}(g))) \in H_{G}^{\square}(I K)$, 有

式中

$\tau$为指标集.

证  由推论3以及定理10可证.

定理11表明，对于不完备背景，我们可以通过其对象近似直观图得到部分的近似概念. 再根据近似概念的上确界运算, 便可以得到所有的近似概念. 具体的求解步骤为:

1) 画出$I K$的对象近似直观图$\left(H_{G}^{\square}(I K), \leqslant\right)$.

2) 对$\left(H_{G}^{\square}(I K), \leqslant\right)$中的元素, 根据定理2中的式(1) 进行运算$\lambda_{\cap}^{}{\circ} \uparrow$.

3) 对步骤2) 得到的近似概念, 根据定理8进行上确界运算便可得其他的近似概念.

例11 (续例10)  对于$\left(H_{G}^{\square}(I K), \leqslant\right)$中的元素$(3, (d, d k))$, 通过定理2中的式(1) 可得

由图 11可以验证$(13, (d, d k)) \in L(I K)$.

本文利用直观图研究不完备背景的三支近似概念和近似概念的获取方法. 首先借助三支近似概念格与某些特定形式背景的概念格的同构关系，通过特定形式背景的直观图给出三支近似概念的获取方法；接着，利用三支近似算子定义的三支近似直观图给出相应的获取方法. 而对于近似概念，采用与三支近似概念获取方法相同的研究方式，从格同构和近似算子两个角度给出相应的获取方法.

另外，文献[20]中已将文献[19]的近似概念归到了部分已知概念的框架下. 关于部分已知概念还有其他两种类型，后续将进一步借助直观图研究其他两类部分已知概念的获取方法.