-
在生态学中,当一个捕食者与食饵共同竞争一种资源时,称出现集团内捕食(intraguild predation).大量生态学证据表明集团内捕食在自然界中是一种广泛存在的生态现象[1-2].通过建立一个三维ODE基本模型,文献[3]对这类问题从理论上做了一些开创性的研究;在文献[3]的基础上,文献[4]进一步全面研究了在双线性(Holling-Ⅰ)功能性反应函数条件下,集团内捕食模型的共存与灭绝等问题;而文献[5-8]则分别考虑了集团内捕食者采用Holling-Ⅱ,Holling-Ⅲ及比例依赖型的功能反应函数的动力学模型,研究了上述各种功能反应函数对集团内捕食系统性态的影响.
注意到上述参考文献没有考虑捕食者种群内部之间的竞争效应,本文引入捕食者的Beddington-DeAngelis型功能反应,通过无量纲化得到如下的模型:
其中:x为共享资源(resource)的密度,在没有捕食者时该资源按logistic增长;y和z分别代表集团内猎物(intraguild prey或IG-prey)与集团内捕食者(intraguild predator或IG-predator)的密度,参数d1和d2分别表示两类捕食者的死亡率;假设所有捕食关系都遵循Beddington-DeAngelis型功能反应,相关参数意义参见文献[9].特别地,参数ei(i=1,2,3) 表示捕食者种群对其自身捕食的干扰强度.
最近,文献[10]对考虑Beddington-DeAngelis型功能反应的非自治集团内捕食系统的周期解问题做了研究,我们指出本文所得到的种群灭绝和系统持久的相关条件和结论与文献[10]有所不同,且我们所得到的部分条件要求更低.
全文HTML
-
引理1 假设
那么模型(1) 满足初始条件(x(0),y(0),z(0))>(0,0,0) 的解(x(t),y(t),z(t))非负且满足
其中
z*为满足方程
的唯一正根.
证 根据比较定理,由初值条件(x,y,z)≥(0,0,0) 易知系统(1) 的解为非负的.从而由第一个方程得:
进而有
即对任意的ε>0,存在一个T(ε)>0,对任意的T>T(ε)有:
从而由系统(1) 的第二个方程我们有
考虑下面的辅助方程
容易证明,如果
${d_1} \frac{{{m_1}}}{{{c_1} + 1}} $ ,则方程(3) 存在唯一的正平衡点且知它在
${\mathbb{R}^ + } $ 上是全局渐近稳定的.从而由比较定理我们有因此存在一个T′(ε)>T(ε),对所有的T>T′(ε)满足:
由系统(1) 的第三个方程,我们有
考虑下面的辅助方程
容易证明,当
时,(4) 式存在唯一的正平衡解z*,且全局渐近稳定.从而根据比较定理我们有
引理证明完毕.
定理1 设模型(1) 满足初始条件(x(0),y(0),z(0))>(0,0,0) 的解为(x(t),y(t),z(t)),则下面结论成立.
(¡)若
${d_1} > \frac{{{m_1}}}{{{c_1} + 1}} $ ,则有(¡¡)若
$ {d_1} < \frac{{{m_1}}}{{{c_1} + 1}}$ 且则有
(¡¡¡)若
$ {d_1} > \frac{{{m_1}}}{{{c_1} + 1}}$ 且则有
且
证 (¡)根据引理1,对于足够大的t,我们有
取
根据系统(1) 的第二个方程,对足够大的t有
因此有
成立.
(¡¡)根据引理1,当
$ {d_1} < \frac{{{m_1}}}{{{c_1} + 1}}$ 时,对充分大的t有取
那么根据系统(1) 的第三个方程,对充分大的t有
从而由比较原理知
(¡¡¡)若
取
则对充分大的t有:
从而由(5),(6) 式及系统(1) 的第三个方程,对充分大的t有
因此有
-
引理2 假设
那么模型(1) 满足初始条件(x(0),y(0),z(0))>(0,0,0) 的解(x(t),y(t),z(t))满足
其中
z*为方程
的唯一正根.
证 由系统(1) 的第一个方程,我们有
由比较定理及假设条件
$\frac{1}{{{e_1}}} + \frac{1}{{{e_2}}} < 1 $ 有从而对于足够小的ε>0,存在Tε,对任意的t>Tε有:
由系统(1) 的第二个方程我们有
考虑下面辅助方程
容易证明,当e3m1x*>(a3+e3d1)(c1+x*)时,系统(9) 唯一的正平衡点y*在
$ {\mathbb{R}^ + }$ 上全局渐近稳定.由比较定理有从而存在Tε′,对任意t>Tε′有
再由系统(1) 的第三个方程有
考虑下面辅助方程
容易证明当
$ {d_2} < \frac{{{m_2}{x_*}}}{{{c_2} + {x_*}}} + \frac{{{m_3}{y_*}}}{{{c_3} + {y_*}}}$ 时,(10) 式存在唯一的正平衡点z*,且该平衡点是全局渐近稳定的.从而由比较定理知证明完毕.
定理2 假设条件(7) 成立,那么系统(1) 存在一个正的全局吸引子[x*,x*]×[y*,y*]×[z*,z*].
证 由条件
$ \frac{1}{{{e_1}}} + \frac{1}{{{e_2}}} < 1$ 知从而y*<y*.因此有
因此若条件(7) 成立,则条件(2) 成立,即引理1和引理2同时成立.从而系统(1) 满足初始条件(x(0),y(0),z(0))>(0,0,0) 的解(x(t),y(t),z(t))同时满足下面的不等式:
这表明[x*,x*]×[y*, y*]×[z*,z*]是系统(1) 的一个正的全局吸引子.证明完毕.
-
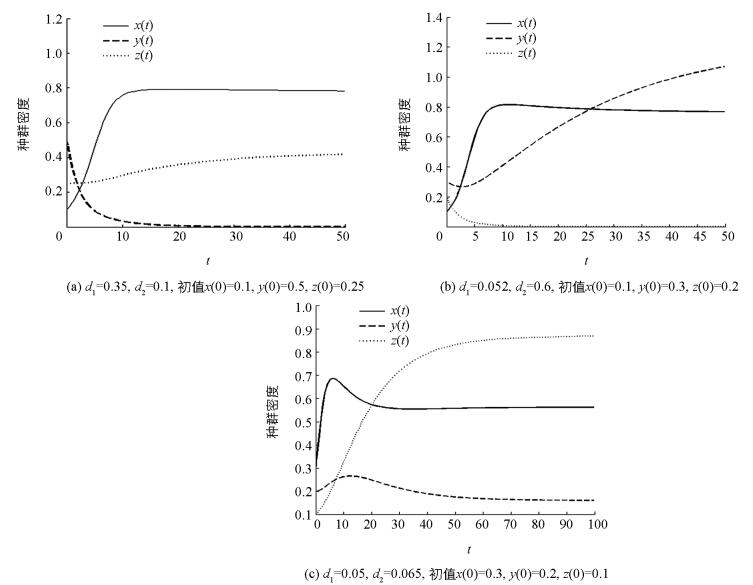
本节对前面结论通过数值模拟进行验证.取定参数m1=0.35,m2=0.25,m3=0.15,c1=c2=c3=0.1,e1=3.5,e2=2.5,e3=1.5, a3=0.2.当d1=0.35,d2=0.1时,定理1(¡)条件成立,则集团内猎物(IG-prey)灭绝(如图 1(a));当d1=0.052,d2=0.6时,定理1(¡¡)中条件成立,则对应集团内捕食者(IG-predator)灭绝(如图 1(b));而当d1=0.05,d2=0.065时,定理2中条件成立,系统(1) 一致持续(如图 1(c)).



 下载:
下载: