-
随着精准农业的发展,越来越多的智能用电设备应用在农业生产领域[1-2],由于受地域特别是山地丘陵地区的限制,电力有效供给是农业智能化过程中面临的突出问题之一.太阳能作为一种重要的清洁能源,适宜在农业生产中推广应用.目前,合理高效地利用太阳能光伏发电已成为农业能源工程研究热点[3-4].
为实现提高太阳能光伏发电效率的目标,在不同的光照度和温度条件下光伏电池需运行在相应的最大功率点(Maximum Power Point,MPP).国内外现有研究成果主要针对光伏电池电压、电流输出曲线的非线性特点,提出了不同的最大功率点跟踪方法[5-12],2011年悉尼大学Dylan等[5]采用分布式最大功率点跟踪(DMPPT)技术来提高发电效率,结果表明光伏电池输出稳态性能得到提高. 2012年亚特兰大大学Thomas Bennett等[6]为提高光伏电池MPPT的快速性,提出忽略光伏并联电阻的光伏等效模型. 2014年马来西亚大学Kok等[7]提出一种新的INC跟踪方法,该方法引入P-V曲线斜率限制条件来优化跟踪步长,从而在光照快速变化的情况下能够提高系统跟踪效率.郭明明等[13]采用改进的变步长电导增量法,实验结果显示跟踪时间约为3.7 s,跟踪效率约为93.33%,能够在一定程度上解决光照大幅变化时系统的震荡现象.栗晓政[14]提出基于分段数值逼近的可变步长电导增量法,MPPT在响应速度和跟踪效率上得到改善,跟踪效率达到95.24%.
本文针对电导增量法跟踪速度和稳态震荡难以兼顾的问题,提出一种具有初值设定的双模式电导增量法.首先,文章从理论上分析了光伏电池开路电压和光照度的关系以及参考电压初值设定对MPPT控制程序跟踪速度的影响;其次,通过双模式控制策略的选择,使光伏系统较稳定地工作在最大功率点附近;最后,本文通过建模仿真并经物理实验平台验证了该算法的可行性.
全文HTML
-
光伏电池是利用光伏半导体材料的光生伏特效应将太阳能转化为直流电能的器件[11],按照不同的功率要求,可以将光伏电池组装成不同规模的太阳能光伏模块.光伏电池的输出功率随着太阳辐射和环境温度的变化呈现出非线性的特点.文献[15]Marcelo GradellaVillalva教授提出了光伏电池的方程.
式中,I是光伏电池输出电流;V是光伏电池输出电压;Rs是光伏电池串联等效电阻;RP是光伏电池并联等效电阻;Iph为光生电流;IOS是光伏电池无光照时饱和电流;A和B是理想因数;T是环境温度(单位:℃);K为玻尔兹曼常数,K=1.381×10-23JK-1;q为电荷数;KI为短路电流温度系数;S是光照辐射强度(W/m2);Isc为光伏电池在25 ℃、光照强度1 000 W/m2时的短路电流;EGO为半导体硅的带隙能量;Tr为参考基准温度;Ior为光伏电池在温度Tr时的饱和电流.
在应用中,一般由多个同性能太阳能电池单体组成光伏模块,光伏模块的输出特性和单个电池单体的输出特性一致[16-17],由(1)、(2)、(3) 式建立随光照度、温度参数变化的光伏模块仿真模型,如图 5所示.
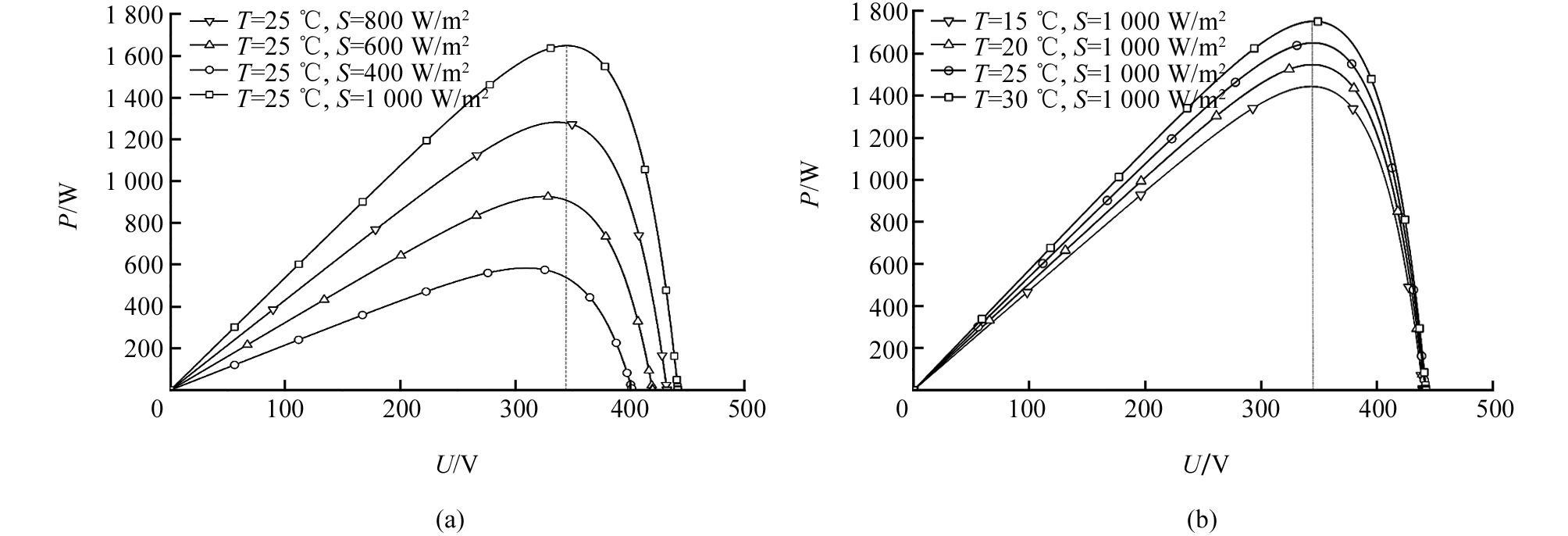
光伏模块输出功率与输出电压之间的关系,简称P-V输出特性,图 1(a)、图 1(b)中的4条曲线分别是在相同温度、不同的光照及相同光照、不同温度条件下所获得的光伏模块P-V曲线.仿真结果和光伏模块输出特性的理论分析相吻合,由图 1可以得出在同一环境状态下,光伏模块有且仅有一个最大功率输出工作点,即MPP.
-
光伏模块的MPPT速度与其设定的参考电压初值Vref关系密切,在MPPT控制程序中,如果Vref无目的设置,Vref不在最大功率点附近时,系统初始化后需要很长时间才能跟踪到最大功率点;Vref设置过大时,将造成系统不能正常工作.其中,Vref是以光伏模块的开路电压Voc为变量的函数.
根据图 1(b)相同光照度,不同温度下光伏模块的P-V曲线,其输出的最大功率点几乎位于垂直线电压附近;但图 1(a)相同温度,不同光照度下的P-V曲线表明光伏模块的开路电压Voc会随着光照度S的变化而变化.所以,为阐明光伏模块开路电压Voc和光照度S之间的理论关系,对(1) 式进行推导.通常光伏电池并联等效电阻RP很大[13],故(V+IRS)/RP项远远小于Iph,可省略. (1) 式变为
由(4) 式得输出电压方程,
令M=[ISC+KI(T-25)]/100,由(3) 式得,Iph=M·S.由(5) 式得开路电压Voc(在I=0条件下),
(6) 式说明光伏模块的开路电压Voc与光照度S的自然对数成正比.由此理论关系,可以在不断开系统负载情况下在线得到任意光强下的系统开路电压Voc,区别于现有文献[9, 13, 18].光伏模块最大功率点电压VMPP与开路电压Voc存在近似的线性关系[19],利用此特性可将光伏模块输出参考电压Vref控制在位于最大功率点附近的某一电压处,使光伏系统开始工作就获得近似的最大功率输出.通常,
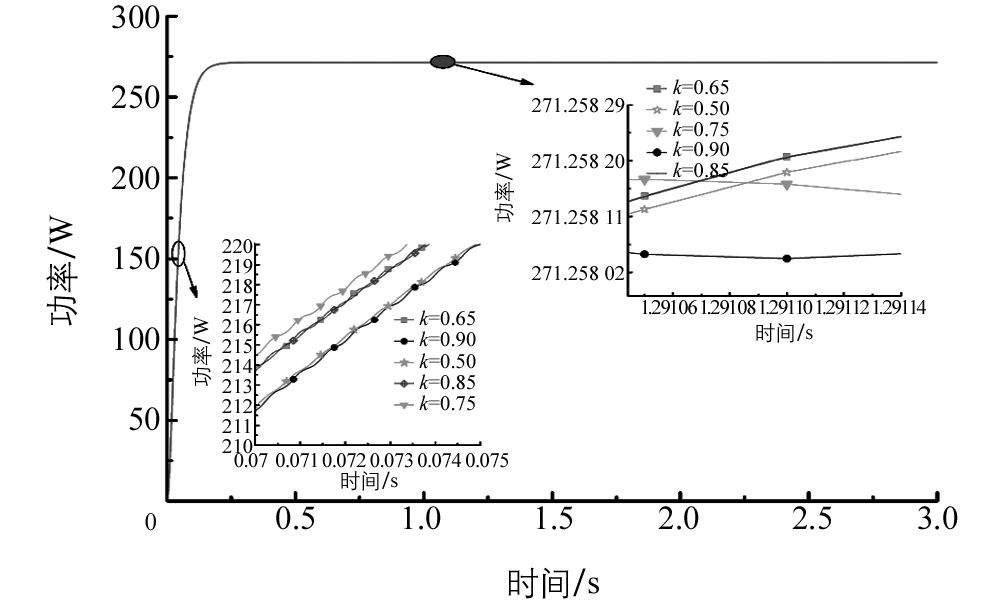
式中,系数K0的取值取决于所用光伏电池的特性,一般取值在0.7~0.8之间.由式(7) 知,系数K0的取值会影响到光伏模块MPP跟踪速度.为了找到合适的系数K0,本文在光照强度800 W/m2,T=20 ℃的条件下对不同的系数K0进行线性迭代实验,结果如图 2所示.由此可知,随着设定的Vref远离系统MPP所对应的电压值时,系统的跟踪速度会相应变慢;K0=0.75为最佳系数,此时Vref位于最大功率点所对应的电压附近.
这种提前逼近的控制方法,易于实现,系统响应速度快,但农业生产环境复杂,外界条件剧烈变化时采用此方法跟踪过程震荡较大.针对这一缺陷,下文中采用具有双模式电导增量法加以优化.
-
电导增量法具有优良的跟踪性能,它是通过比较光伏电池的瞬时电导和电导的变化量来控制ΔV,ΔV称为跟踪步长.由图 1光伏模块P-V特性曲线可知,在最大功率点右侧,dP/dV<0;在最大功率点左侧,dP/dV>0;在最大功率点处,dP/dV=0.已知光伏模块的输出功率P=V·I,对其两端关于电压进行求导,且在最大功率点处有,
式(9) 表明当输出电导的变化量等于输出电导的负值时,光伏模块工作在MPP状态.电导增量法的最大优势在于光照强度变化时[20],光伏模块输出电压能以较平稳的方式跟踪其变化,稳态震荡较小.但在外界温度和光照条件瞬间变化的情形下,步长ΔV选择不当会影响MPP跟踪精度.
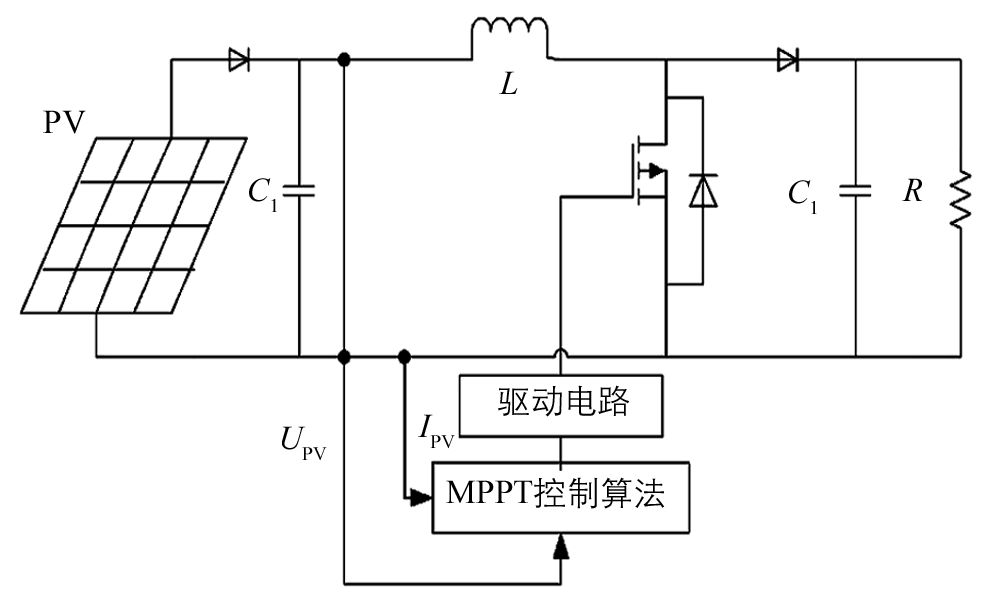
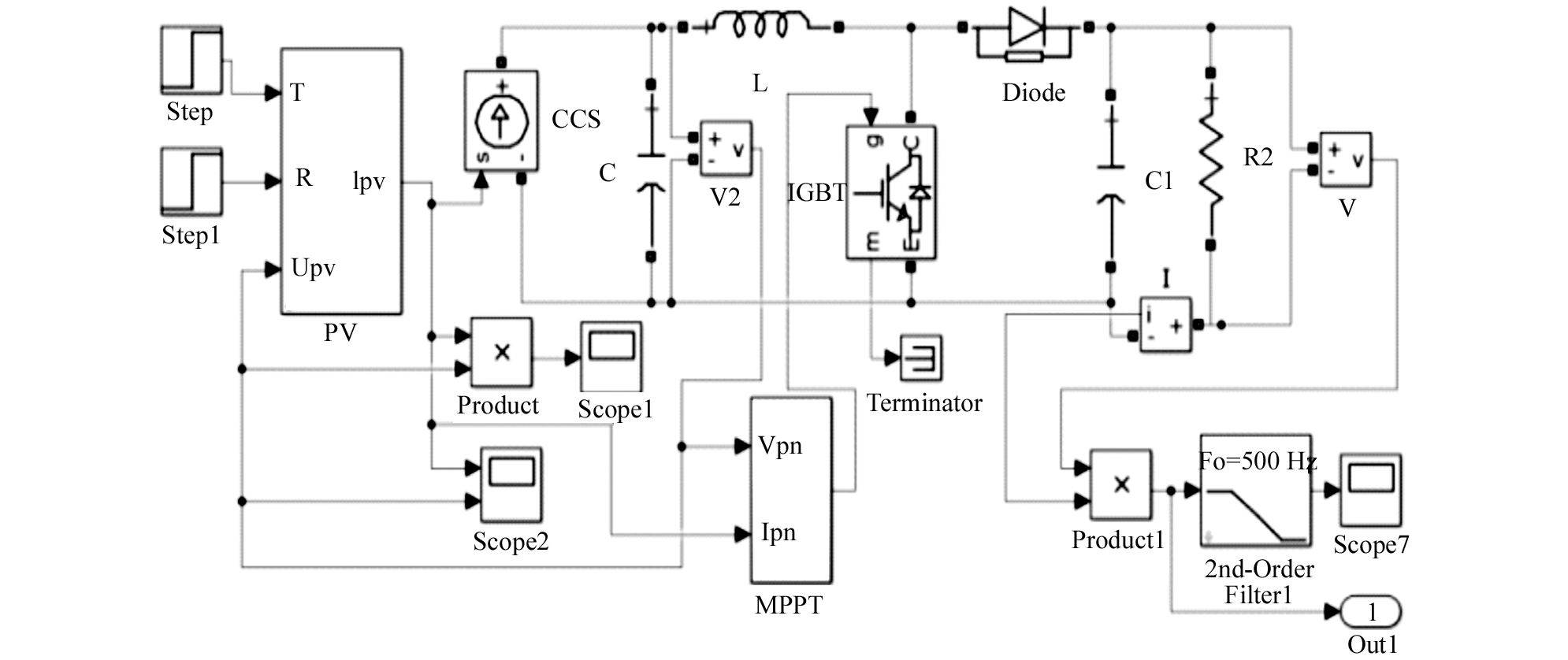
鉴于电导增量法在光伏模块最大功率点跟踪过程中存在的优势和不足,本文提出了一种具有设定电压初值的双模式电导增量法,采用该算法对光伏模块进行最大功率点搜索和跟踪,系统控制电路如图 3所示.
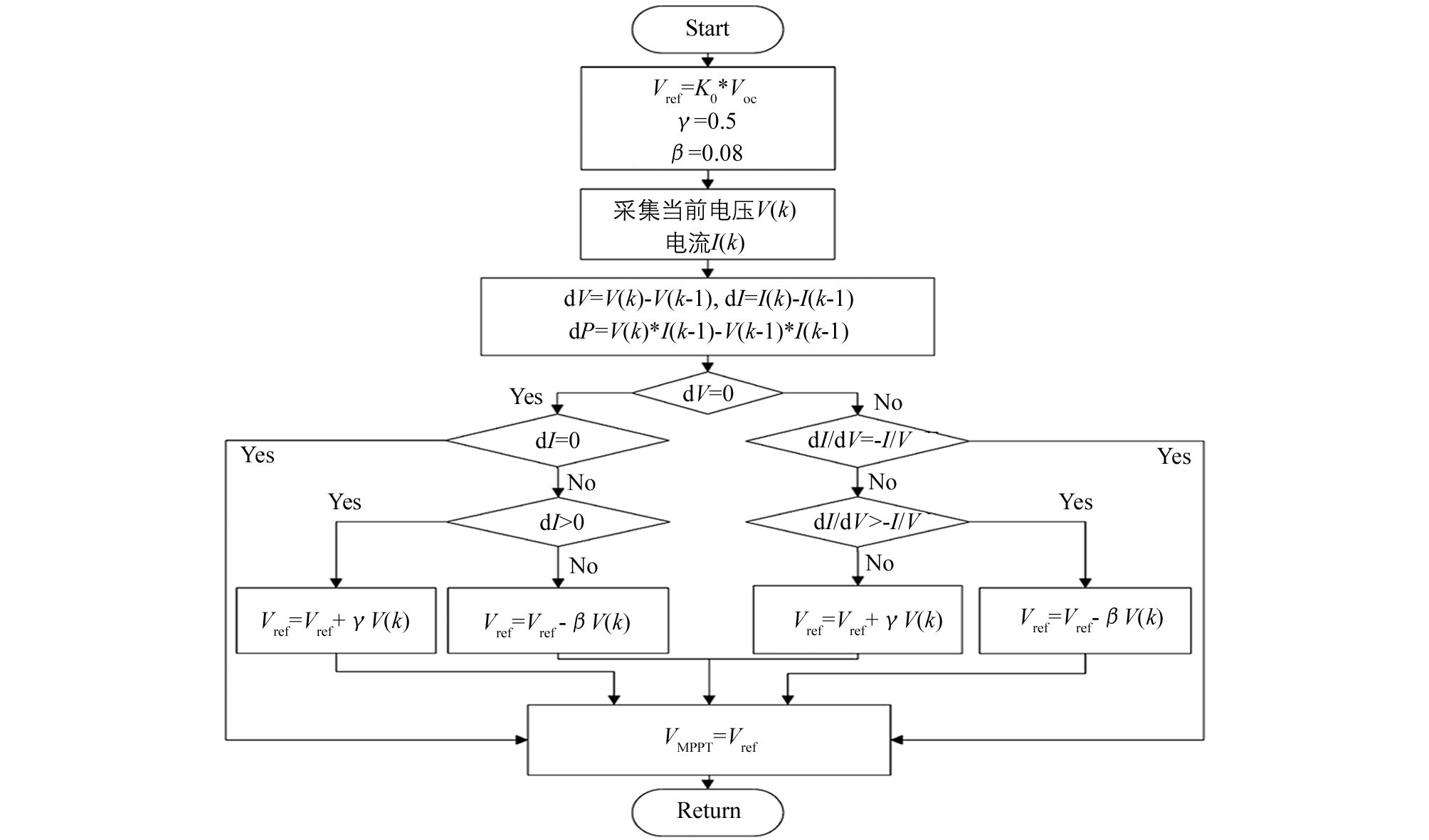
改进算法首先利用式(6) 和式(7) 设定MPPT控制程序的电压初值Vref,使光伏模块开始工作就获得近似的最大功率输出.其次,由光伏模块的输出特性曲线知,在最大功率点左侧,曲线较为平滑,dP/dV变化相对平缓,引入步长缩放因子γ,使用大步长快速跟进;在最大功率点右侧,dP/dV变化相对较大,引入步长缩放因子β,此时使用小步长精确跟踪并稳定在最大功率点.两种控制模式交叉使用提高了MPP跟踪性能,程序流程图如图 4所示.
为了量化评估基于该算法的光伏系统MPPT性能以及使用该控制算法前后系统获取能量的能力,引入量化指标ηMPPT和ζMPPT,由此可以定量分析系统在不同环境以及环境突变情况下的跟踪效率和电能提高百分比.ηMPPT和ζMPPT定义如下,
其中,t0,t1分别表示系统开始运行和结束的时间;Preal表示光伏模块在MPPT算法下实际输出功率;Pmax表示光伏模块在MPPT算法下稳定输出时追踪到的最大功率;Wcontrolled表示施加控制算法后,系统在t0-t1时间内所获取能量;Wuncontrolled表示未施加任何控制算法,系统在t0-t1时间内所获取能量.
2.1. 参考电压初值设定对跟踪速度的影响
2.2. 具有设定电压初值的双模式电导增量法
-
为验证外界环境快速变化时该算法的有效性,对该算法进行了计算机仿真和物理实验平台验证.本文研究实验条件设为:取k0=0.75,γ=0.5,β=0.08;参照型号JT255PLe的实验光伏模块参数,设定仿真模型开路电压37.7 V,短路电流8.98 A.计算机参数CPU为Intel i5-2430M,2.4 GHz,4 G内存,Win7 32bit操作系统,代码编写和仿真平台为MathWorks公司的Matlab2014rb.为达到计算机仿真结果和物理实验结果交叉验证,实验环境统一设定:强光照11 350 Lx(16.62 W/m2),弱光照5 596 Lx(8.19 W/m2),环境温度25 ℃.
-
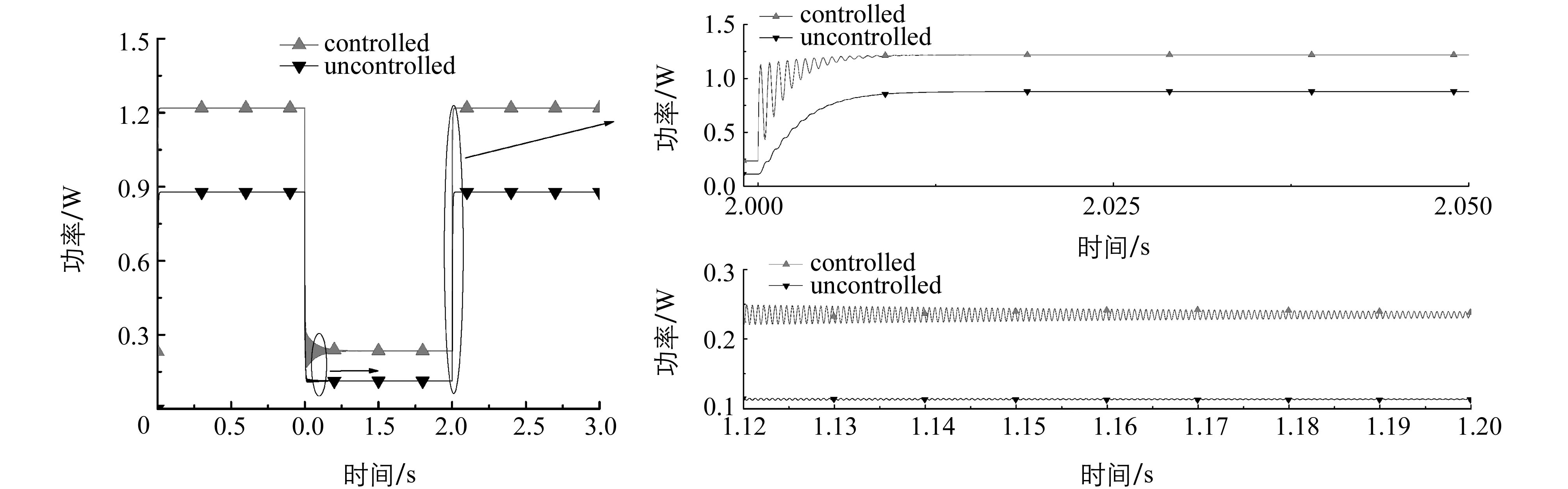
建立光伏系统仿真模型如图 5所示,对该算法在光照度连续突变下的性能进行仿真验证.光照度在t=1 s时刻由16.62 W/m2变为8.19 W/m2,t=2 s时刻由8.19 W/m2变为16.62 W/m2,两次光照度突变情况下光伏模块的开路电压Voc发生变化,控制算法中电压初值Vref自动重新设置,控制系统会在新的MPP处先采用大步长跟踪,然后小步长逼近,仿真结果如图 6所示.
仿真结果讨论分析:仿真结果验证了该算法的可行性.光照度两次突变时,光伏系统在该算法控制下大幅度向此刻的最大功率点逼近,追踪时间分别为0.27 s和0.15 s,较快呈稳态输出并有较强的爬坡能力,减少了震荡现象.仿真性能数据见表 1.
-
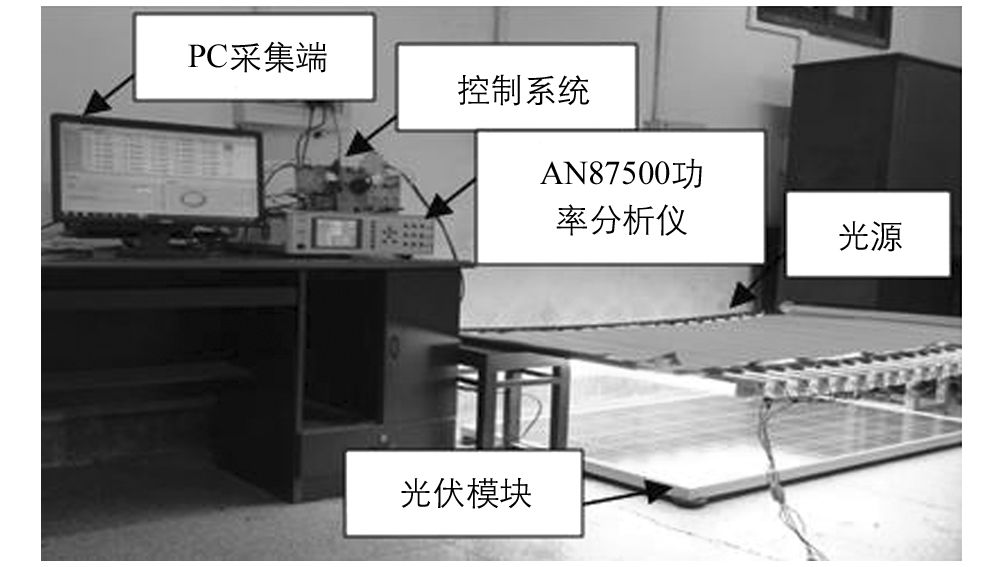
鉴于室外光照度不能突变,人为遮挡制造突变环境易出现不可控因素,为减少实验误差,精确控制环境中光照度的变化,在实验室内设计一套实验平台,如图 7所示.采用20只36W飞利浦日光灯来代替阳光,日光灯均匀分布(间隔5cm)并上覆反光锡纸以增加光源利用率.利用开关A和开关B分别控制标有奇数和偶数的日光灯(以下简称奇数灯和偶数灯)同时点亮或熄灭,在8个均匀分布的光照固定采样点测得光照数据,求其平均值如表 2所示.实验中设置偶数灯长亮,通过开关A控制奇数灯瞬间点亮或熄灭来完成实验测试过程,测试数据通过AN87500功率分析仪实时传回PC端储存.分析仪控制界面如图 8所示.
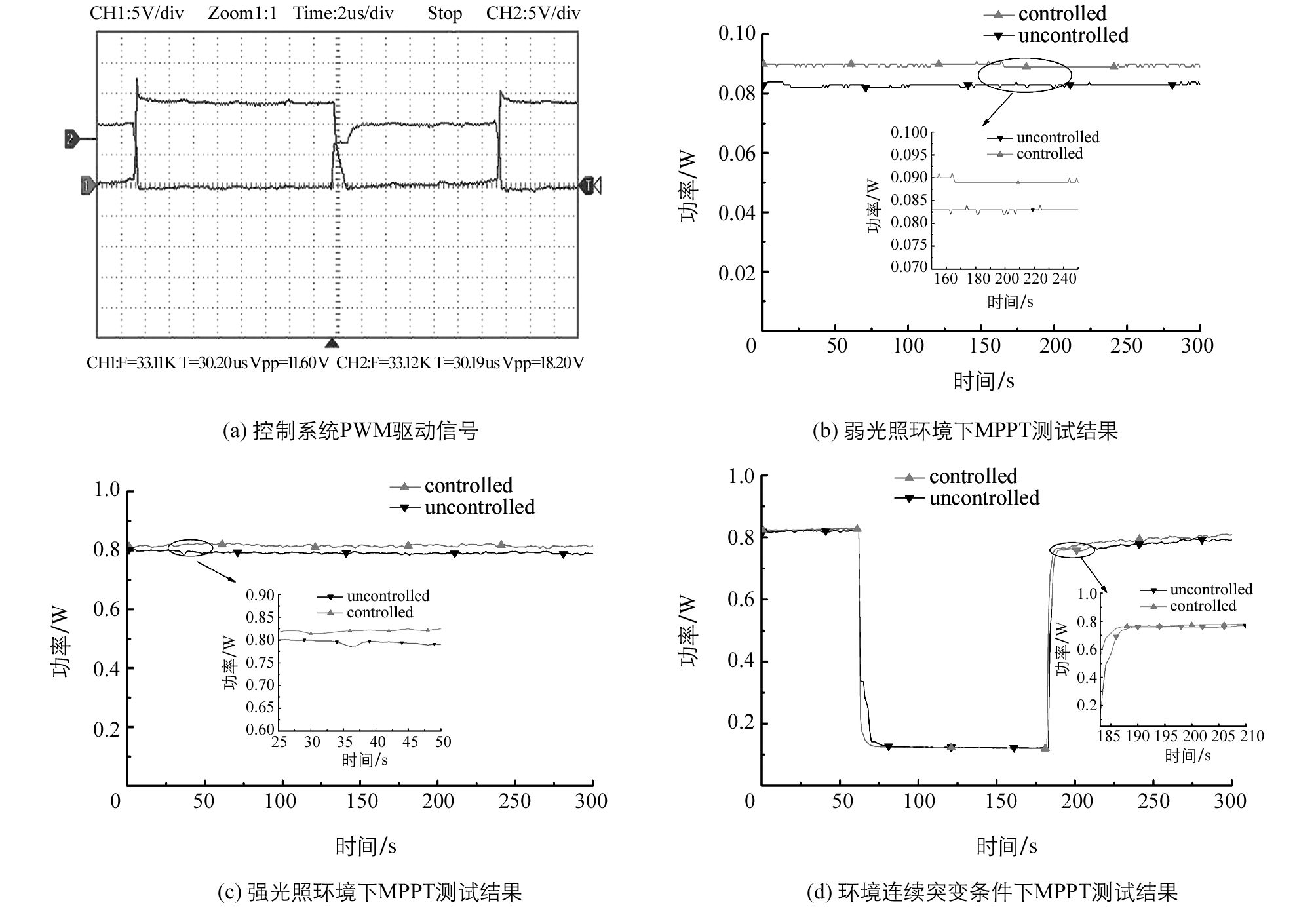
实验测试分别在弱光照(10盏灯光照度5 596 Lx)、强光照(20盏灯光照度11 350 Lx)、光照突变(20盏灯——10盏灯——20盏灯) 3种环境下进行,每组测试时间为300 s.测试结果如图 9所示,系统性能指标测试数据如表 3所示.
实验结果讨论:图 9(a)为控制系统PWM驱动信号,其占空比依据采样电压电流信号而变. 图 9(b)、图 9(c)分别为光伏系统在弱光照和强光照环境下测试结果,施加控制算法前后,系统获取能量较未加控制算法时分别提高3.900%、3.724%;稳态输出时,本MPPT控制算法效率分别达到95.690%、97.826%,与文献[13]和文献[14]相比,弱光照和强光照两种环境下算法效率都有所提高,有效减少了稳态输出震荡. 图 9(d)为光伏系统在环境突变下测试结果,施加控制算法前后,系统获取能量提高3.666%,两次追踪时间分别为3.01 s、3.99 s,追踪均值时间比文献[13]提高约0.2 s;稳态输出时,本MPPT控制算法效率为95.868%,与文献[20]所提出的MPPT控制算法效率95.09%相比,提高了0.778%,环境突变情况下适应性较强并有效减少了稳态输出震荡.
3.1. 光照度连续突变条件下的系统性能仿真实验
3.2. 实际环境条件突变时系统性能验证
-
1) 针对光伏发电系统MPPT算法在跟踪速度和稳态震荡上难以兼顾的问题,文章推导了光伏电池开路电压和光照度的数学关系,建立两者之间的数学模型,提出了一种具有初值设定的双模式电导增量法,并说明了光伏系统开路电压Voc与电压设定初值Vref存在线性关系,对不同的系数K0进行线性迭代实验取最优值.
2) 光伏系统在不同光照环境下测试,通过所给出的公式进行量化评价.大量的实验数据表明,所提算法是一种有效的光伏模块MPPT算法.在农业生产中将本算法用于采用光伏发电供能的智能设备,能够提高单位时间光伏模块发电量,具有现实意义.
3) 通过大量仿真实验数据和物理实验数据交叉比较表明,计算机仿真从理论上验证了所提算法的可行性;物理实验从工程应用上验证了所提算法的正确性和实用性.但是,由于物理实验中电路元件存在能量消耗以及开关器件制造工艺存在误差,光伏发电系统的物理实验未完全达到仿真实验的理论效果.
实验测试过程中,跟踪步长系数γ,β是根据光伏电池P-V特性曲线MPP左右两侧斜率不同,通过多次模拟手动调节到最佳效果为止,跟踪步长系数γ,β的微机智能设置将是下一步研究工作所关注的问题.



 下载:
下载: