-
近年来随着医学影像技术突飞猛进的发展,医学图像为临床诊断提供了较好的诊断依据.在许多重要的医学临床应用中,可以通过医学图像匹配的方法对患者的医学影像进行空间匹配,以帮助医生更好、更准确地为患者进行诊断并制定出治疗方案[1-2].
为了追求更准确的医学图像匹配结果以及获取更高效的医学图像匹配方法,国内外较多的专家学者对医学图像匹配算法进行了深入的研究,主要的医学图像匹配算法有SIFT(Scale-invariant feature transform)、SURF算子以及图形上下文等方法,如Huisi等人[3]通过对SIFT算法进行研究,提出了基于三维SIFT提取脑部图像中正中矢状面方法的研究,利用SIFT算子提取脑部图像的特征点及生成特征描述子,进而完成对脑部图像中正中矢状面的匹配.但由于SIFT算子的鲁棒性不佳,当图像存在诸如噪声等几何攻击时,提取的特征点中存在较多的伪特征点,易导致其匹配准确度不高,且直接利用SIFT算子提取的图像特征空间维数较高,易降低其匹配效率.为此,李冠宇等人[4]通过对SIFT方法进行改进,提出了一种改进的SIFT血管图像特征匹配算法,利用SIFT算子提取特征点,并对其进行降维处理,从而降低了算法的计算复杂度,最后根据IVUS(Intravascular Ultrasound)图像的特征点,对其梯度幅度进行约束,完成图像匹配.虽然该技术对SIFT算子进行了改进,但是SIFT仍然缺乏鲁棒性,且梯度幅度缺乏敏感性,当原图像存在小尺度变换时,其像素梯度幅度的变化较小,使其匹配提纯效果不佳.
因此,为了克服SIFT算子的不足,并提高医学图像的匹配精度,李军伟等人[5]通过对基于图形上下文的方法进行研究,提出了一种基于颈动脉粥样硬化斑块的多序列MR图像去噪与配准算法,该算法利用改进的小波变换方法对核磁共振图像进行去噪;然后,再用shape context方法生成特征描述子;最后通过建立代价函数模型对特征点进行匹配,利用特征点之间的距离约束来优化匹配特征点,实现MR图像的精确匹配.虽然该技术能够获得较高的医学图像匹配精度,但是该算法使用了代价函数模型,计算复杂度较高,导致MR图像匹配时效率不理想.为了兼顾匹配精度与效率,刘桥等人[6]提出了一种基于SURF算法的医学图像特征点匹配算法,采用SURF算法提取特征点后,再通过Haar小波变换生成特征描述子,最后,通过改进的最近邻搜索方法完成特征点匹配,并通过随机抽样一致性来删除错误匹配特征点,实现医学图像特征点的匹配.但该方法过度依赖阀值,导致其抗干扰能力较差.
因此,本文提出了一种基于移动队列规则耦合角度约束的医学图像匹配算法.该算法采用高斯金字塔模型对源图像进行预处理,以提高源图像的质量,提升算法的匹配准确度;利用Harris算子对预处理后的源图像进行特征点提取;再通过SURF机制,获取特征点的主方向以及特征向量,生成特征描述子;利用尺度空间理论得到的特征点集来形成特征队列,定义移动队列规则,完成特征点的匹配;且利用特征点之间形成的夹角构造角度约束模型,对错误匹配特征点进行剔除,从而达到对匹配特征点进行提纯的效果,进一步提高了算法的匹配准确度以及鲁棒性;最后,测试所提算法的匹配精度.
全文HTML
-
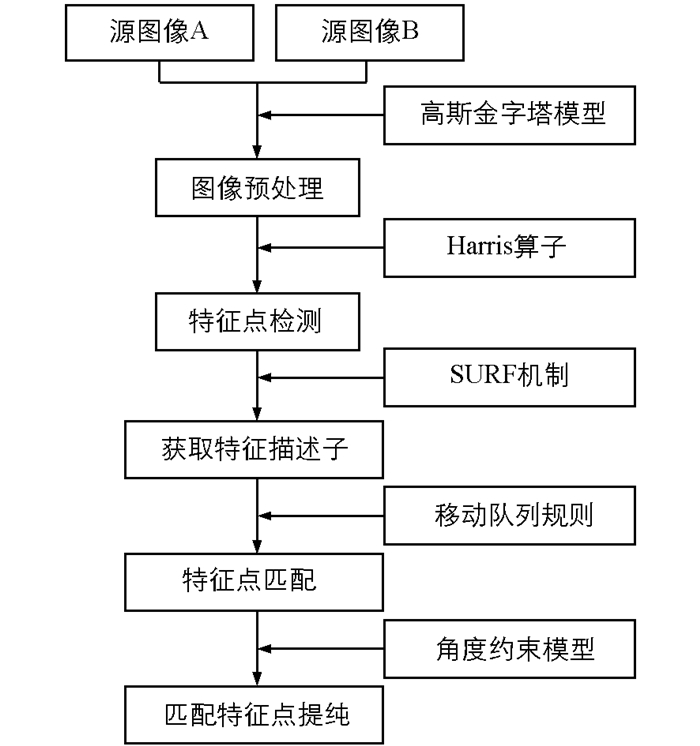
本文提出的医学图像匹配算法过程见图 1.从图 1可知,本文算法主要由5个部分组成,分别是图像预处理部分、特征点检测部分、获取特征描述子部分以及特征点匹配部分和匹配特征点提纯部分.在图像预处理部分,通过高斯金字塔模型对源图像中的噪声等干扰信息进行滤除,以提高算法的匹配准确度与鲁棒性;在特征点检测部分,利用Harris算子对特征点进行检测,以提高算法的匹配精度;随后,通过SURF机制来获取特征点对应的主方向以及特征向量,以生成特征点对应的特征描述子;最后,通过设计移动队列规则完成特征点的匹配,并基于特征点夹角的角度约束模型对伪匹配特征点进行剔除,进一步提高算法的匹配准确度.
-
为了滤除医学图像中的噪声等干扰信号,增强图像的质量,为后续的操作提供更好的图像源,本文采用高斯金字塔模型对源图像进行预处理.
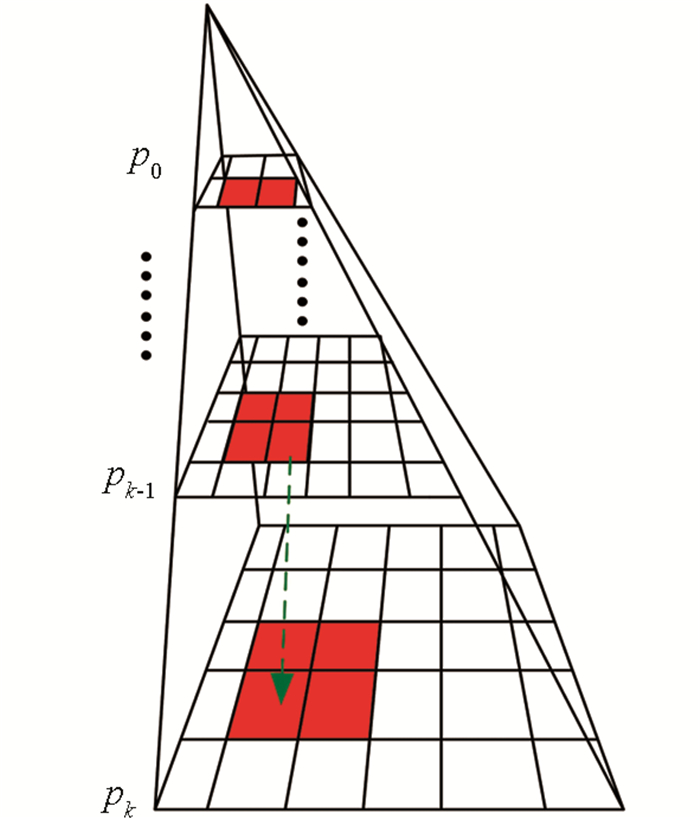
高斯金字塔由多层构成,顶层图像为初始源图像,往下每一层的图像都为上一层经过滤波后形成的新图像,其过程如图 2所示.设高斯金字塔的顶层图像为P0,则第k层的递归结果可通过高斯滤波核β构成的高斯金字塔模型来表示.高斯金字塔模型表述如下[7-8]:
通过对源图像进行滤波,将源图像中存在的噪声等干扰信号进行滤除,以形成质量更为优良的新图像,提高了算法的匹配准确度以及鲁棒性.
-
源图像预处理后,对所得的新图像进行特征点检测. Harris算子具有检测精度高以及检测效率高等特点,能对源图像中的特征点进行精确快速的检测[9].为此,本文采用Harris算子对预处理后所得的源图像进行特征点检测.首先,对于以图像中的任意一个像素点D(x,y)为中心的矩形窗口,在横坐标与纵坐标上分别移动L和V个单位后,其对应的灰度信息变化值TL,V为[10-12]
其中,W表示高斯滤波器,F表示图像灰度函数.
对(2)式进行展开可得
再将(3)式进一步转化为二次型,即
其中,G为实对称矩阵,则
当G的行列式和迹分别为DET(G)和TR(G)时,可得特征点的检测函数为
其中,θ为任意微小常数.
通过式(6),求取各个像素点的PT值,若某一点的PT值大于设定的阀值FPT,则判定该点为特征点.
-
对图像的特征点检测完毕后,再获取特征点对应的特征描述子. SURF机制获取的特征描述子具有较低的维度以及较好的鲁棒性.对此,本文采用SURF机制获取特征描述子,其过程分为主方向以及特征向量的获取.
在SURF获取特征描述子机制中,主方向的获取过程为:首先,将尺度值为s的特征点作为圆心,构造出一个半径为6s的圆;然后,利用边长为4s的Haar小波计算出该圆位于x和y轴方向上的Haar小波响应值,并对这些响应值进行高斯加权处理;最后,滑动一个π/3的扇形窗口对构造的圆进行遍历,并计算窗口内x和y轴方向上Haar小波响应的总和,从而形成一个向量集,选取向量集中最大值对应的方向作为主方向[13-14].
SURF的特征向量的获取过程为:首先,以特征点为中心沿着主方向选取一个边长为20s的矩形区域,并将其分成4×4个子域;然后,利用边长为2s的Haar小波对每个子域计算水平与垂直方向上的Haar小波响应,其结果分别用Hx与Hy表示;最后,在每个子域对Hx、Hy以及|Hx|、|Hy|进行求和运算,可得一个4维向量:
综合4×4个子域,可得到4×4×4维的向量,将此64维向量进行归一化处理后就可得到具有旋转、光照等不变性的特征向量[15-16].
-
当源图像A在某一尺度下检测到的多个特征点,分别对应于源图像B在不同尺度下检测到的特征点时,将会造成图像的匹配精度下降.为了提高算法的匹配精度,本文基于尺度空间理论,将源图像A组成具有m个特征集的队列QA,源图像B组成具有n个特征集的队列QB,并将QA和QB中的特征集按照尺度值大小升序排列,从而制定了移动队列规则,将2个特征集队列中的每个特征集都利用欧氏距离度量一遍,然后将匹配特征点个数最多的特征集对应的匹配特征点作为最终的匹配特征点.其具体过程如下:
首先,将队列QA中的第一个特征集与QB中的第n个特征集对齐,接着借助欧氏距离度量方法,通过计算特征点的最近邻与次近邻比值,统计QA中的第一个特征集与QB中的第n个特征集所对应的匹配特征点个数[17];
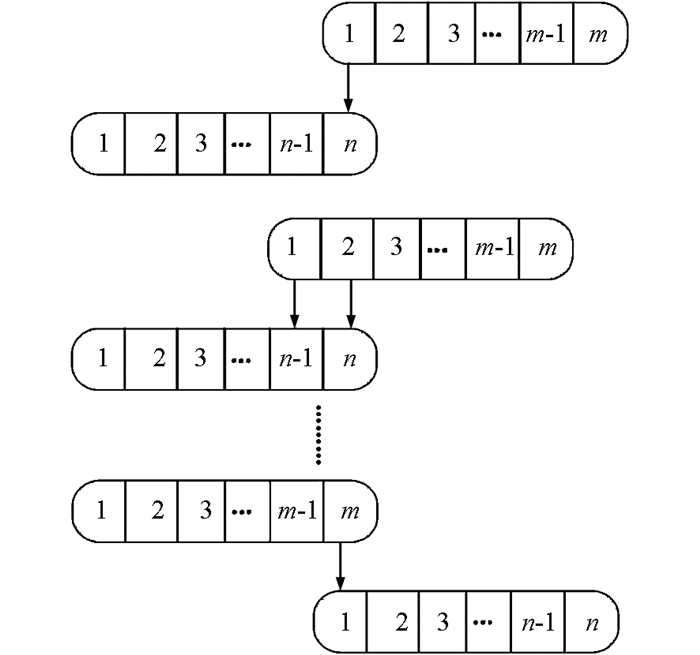
然后,以队列QB为基准,一个特征集为步长,将队列QA进行左移,并且每移动一次,都将按照最近邻与次近邻相比的方法求取队列QB、QA中匹配的特征点个数.直到队列QA中的第m个特征集和队列QB中的第一个特征集对齐为止.该移动队列的过程示意图如图 3所示;
最后,对QA和QB中形成的特征集对的匹配特征点个数进行比较,将匹配特征点个数最多的特征集对的匹配特征点,作为源图像A和源图像B的最终匹配特征点.
-
由于一幅图像中特征点之间形成的拓扑关系,与另一幅图像中对应的匹配特征点处形成的拓扑关系有相近关系[18].可以通过选取3对匹配特征点,以这3对匹配特征点之间的夹角来构造角度约束模型,来约束特征点对应的拓扑关系,完成对匹配特征点的提纯.因此,本文利用特征点之间形成的夹角关系,构造了角度约束模型,剔除错误的匹配特征点.
设源图像A中的点R1(i1,j1)、R2(i2,j2)、以及R3(i3,j3)分别和源图像B中的点R′1(i′1,j′1)、R′2(i′2,j′2)、以及R′3(i′3,j′3)为匹配特征点.假设点R1(i1,j1)、R2(i2,j2)、以及R3(i3,j3)形成的夹角为Φ,点R′1(i′1,j′1)、R′2(i′2,j′2)、以及R′3(i′3,j′3)形成的夹角为Φ′,根据余弦公式可得[18-19]
通过(8)式和(9)式可求得夹角Φ以及Φ′的值,继而构造如下角度约束模型:
其中,TP为预定的约束阀值.
当源图像A中与源图像B中对应的3对匹配特征点形成的角度满足角度约束模型时,则判定这3对匹配特征点为正确匹配特征点,然后,任选2对匹配特征点作为后续判定的基准点.每加入1对新的匹配特征点都要用角度约束模型进行判定,若不满足角度约束模型,则新加入的匹配特征点对将被剔除,从而完成匹配提纯.
1.1. 图像预处理
1.2. 特征点检测
1.3. 获取特征描述子
1.4. 特征点匹配
1.5. 匹配特征点提纯
-
为了验证所提算法的优异性,将当前医学匹配精度较高的技术视为对照组:文献[20]、文献[21].其中,文献[20]在SIFT机制的基础上,引入了相似块结构对其进行改进,有效地提高了其特征检测精度,增强了其技术的鲁棒性;文献[21]则是通过改进Harris算子来提高特征点的检测精度与效率,同时,利用双向异步的投票策略与RANSAC机制来提纯匹配精度.因此,文献[20]、文献[21]在医学图像匹配领域具有良好的代表性.随后,借助配置为Core i3,2.8 GHz的CPU,内存为8 GB,硬盘为500 GB的硬件平台,采用VC 6.0软件进行仿真实验,对本文所提出的图像匹配算法的效果及性能进行测试.
-
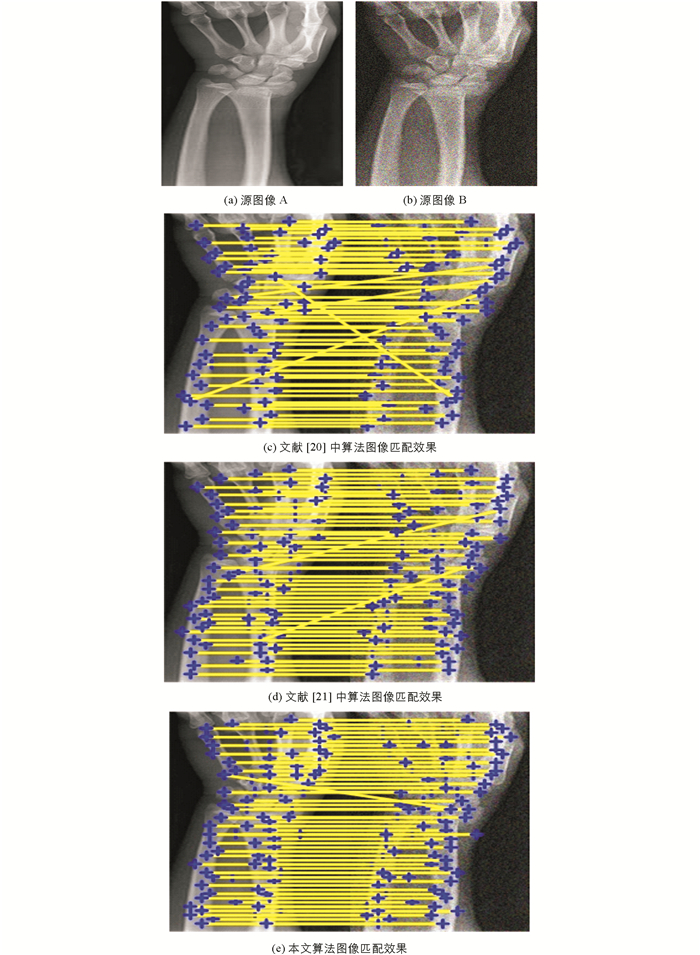
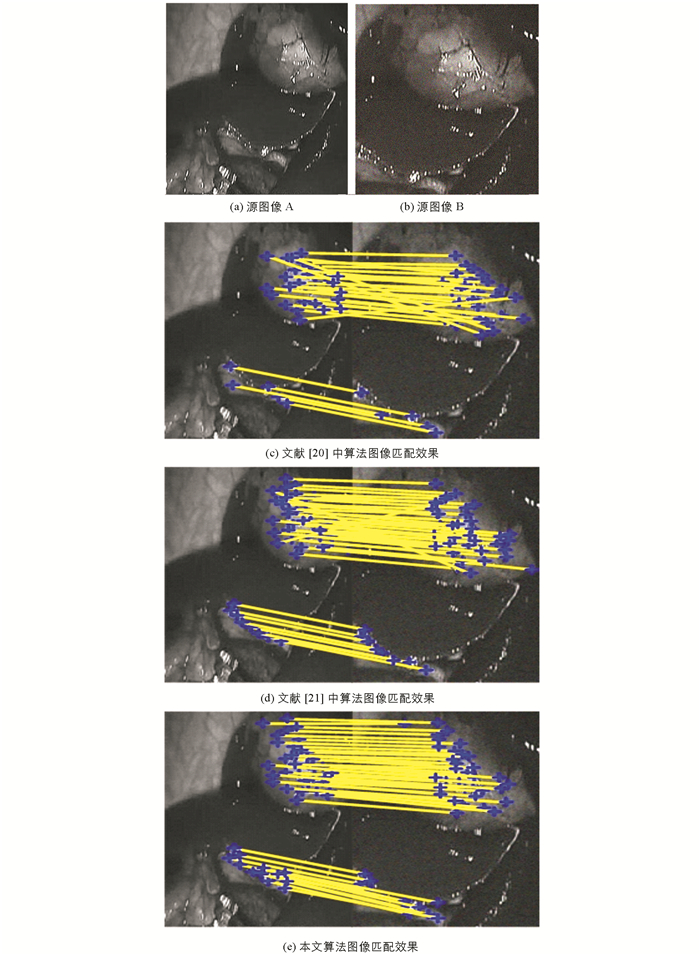
各算法的匹配效果测试结果如图 4和图 5所示. 图 4为对存在噪声干扰的X线图像进行匹配的效果图,图 5为对存在噪声和缩放叠加干扰的心脏图像进行匹配的效果图.从图 4和图 5可知,本文算法的匹配效果(见图 4(e))比文献[20](见图 4(c))以及文献[21]中算法的匹配效果(见图 4(d))更好,具体表现为本文算法的匹配结果中具有更多的匹配特征点,而且存在的错误匹配特征点也最少,说明本文算法较对照组算法具有更好的匹配准确度以及匹配精度.通过对比图 5可知,本文算法的匹配结果(见图 5(e))与文献[20](见图 5(c))以及文献[21]中算法的匹配结果(见图 5(d))相比,存在匹配点数最多,错误匹配点数最少的特点.说明本文算法较对照组算法具有更好的鲁棒性能.究其原因为本文采用了高斯金字塔模型对源图像进行了预处理,有效地抑制了噪声等干扰因素,提高了算法的鲁棒性能以及算法的匹配准确度.同时,本文还采用了Harris算子对特征点进行准确的检测,以及构造了移动队列规则用于特征点匹配,提高了算法的匹配准确度.
-
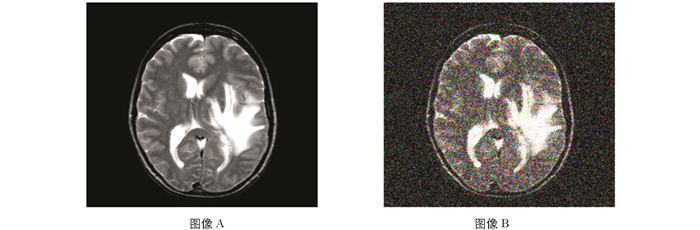
通过用不同算法对测试图像进行匹配,然后记录其匹配耗时以及匹配特征点数量,来体现不同图像匹配算法的性能.测试过程中将特征点总数设为210个.测试图像如图 6所示,其中源图像A为脑部的核磁共振图像,源图像B是将20%高斯噪声施加于源图像A得到的图像.
不同算法的图像匹配性能测试结果如表 1所示.从表 1中可见,本文算法的匹配耗时为3.578 2 s,文献[20]和文献[21]中算法的匹配耗时分别为5.892 1 s以及4.021 3 s,由此可见,本文算法的匹配效率最高.同时通过表 1可知,本文算法的匹配特征点个数为184个,而文献[20]和文献[21]中算法的匹配特征点个数分别为142个以及168个,由此可见,本文算法具有更高的匹配精度.因为本文采用了SURF机制生成了维度较低的特征描述子以及采用了Harris算子对特征点进行了准确快速的提取,提高了算法的匹配效率,同时本文还采用移动队列规则对特征点进行匹配,以及构造了角度约束模型用于对匹配特征点进行提纯,提高了算法的匹配准确度.文献[20]中利用SIFT机制获取特征点以及生成特征描述子,由于SIFT获取的特征点中存在较多的伪特征点,并且SIFT机制获取的特征描述子维度较高,导致文献[20]中算法的匹配准确度不高,算法的匹配效率也不理想.文献[21]中利用双向异步投票策略对特征点进行匹配,然后利用RANSAC优化算法剔除误匹配,完成图像的匹配.由于双向异步投票策略计算复杂度较高,而且RANSAC算法存在计算数据量大以及鲁棒性不高的缺点,导致文献[21]中算法的匹配效率以及匹配精度不佳.
2.1. 图像匹配算法的效果测试
2.2. 图像匹配算法的性能测试
-
为了提高医学图像的匹配精度以及匹配效率,本文提出了一种基于移动队列规则耦合角度约束的医学图像匹配算法.利用高斯金字塔模型对源图像进行了优化,为后续图像匹配步骤的优质完成提供了保障;利用Harris算子准确快速地获取了图像的特征点,提高了算法的匹配精度以及匹配效率;通过SURF机制获取了较低维度的特征描述子,进一步提高了算法的匹配效率;利用移动队列规则对特征点进行匹配,改善了算法的匹配精度;利用特征点之间的夹角构造了角度约束模型,对匹配特征点进行了优化,提高了算法的匹配准确度.



 下载:
下载: