-
火星是太阳系中最接近地球的一颗类地行星,自从发现存在水冰开始,已成为人类的可移居家园,各航天大国开启了各自的火星探测计划[1].由于火星距离地球较远,对火星探测器进行远距离测控的难度较大.尽管世界主要航天大国对火星进行了多次探测,积累了不少数据,但火星重力场模型的分辨率仍然有限.由于火星两极存在一定的干冰,干冰随火星季节发生质量迁移,导致火星重力场呈现出一定的时变特征.影响火星探测器精密定轨的摄动源之一即是火星重力场的非球形引力摄动,重力场模型分辨率的不足,以及重力场模型展开系数时变特征的不精确性,阻碍了火星探测器的精密定轨和火星着陆器的安全登陆[2].
自1962年前苏联发射第一颗火星探测器——火星1号开始,美国紧随其后开展了一系列火星探测任务.火星全球重力场模型的第一次获得是靠美国1996年发射的“火星全球勘测器”(Mars Global Surveyor,MGS),随后于2001年美国又发射了“火星奥德赛”(Mars Odyssey,ODY)探测器.利用两次任务及其拓展任务期间的轨道跟踪数据,美国“喷气实验室”(Jet Propulsion Laboratory,JPL)和“达德航天飞控中心”(Goddard Space Flight Center,GSFC)解算了一系列的火星全球重力场模型MGS85F和GGM1041C等,这些模型的最大展开阶次不足100阶次[3-4].为了获得更高分辨率和时变特征的火星重力场模型,以及高分辨率的火星地形立体图像,美国于2006年发射了轨道高度为255 km×320 km的近极轨道卫星(Mars Reconnaissance Orbiter,MRO).利用MRO探测器2006至2015年期间的所有轨道跟踪数据,综合MGS和ODY早期的轨道跟踪数据,JPL解算了120阶次的最新高阶火星重力场模型MRO120D[5].该模型在高阶项与火星地形的相关性得到了显著的加强,特别是在火星南极地区,重力场模型的有效阶次得到了显著的提高.
我国的火星探测计划起于2007-2011年与俄罗斯合作的、因俄方卫星故障而失败的“萤火一号”火星探测计划[6-7].尽管该计划未能圆满完成,但它表明我国初步建立的全球性深空探测网已经可为远距离测控提供技术支持. “十三五”规划已表明,深空探测将成为未来5年的重要发展方向,火星探测计划已提上日程,我国预计于2020年左右发射火星探测器.由于我国没有发射火星探测器的经验,对火星探测器的影响因素了解较少,探测器定轨高度过高,则不能实现科研价值,过低的轨道高度则可能缩短探测器的在轨时间.另外,国内外目前暂无有关最新火星重力场模型MRO120D对火星探测器影响的研究,利用最新模型MRO120D,并考虑多种摄动因素,对探测器不同轨道高度的在轨时间进行分析,有助于选择合理的轨道高度,对后期火星探测器的成功定轨具有重要意义.为此,本研究利用动力学方法和最新的火星重力场模型MRO120D,在探测器运动的轨道方程中,考虑火星中心引力及其非球形引力摄动,太阳、地球引力摄动,木星、水星、金星等大行星的引力摄动,火卫一Phobos和火卫二Deimos的引力摄动,基于火星大气模型DTM-Mars[8]的大气阻力摄动,太阳光压摄动,以及相对论效应等,对220 km和150 km初始轨道高度的火星探测器进行仿真分析,以期为即将开展的火星探测任务提供一定程度的参考.
全文HTML
-
火星是一个质量积聚体,对其外部空间存在引力作用.为了方便表示,根据广义傅里叶展开理论,通常将火星重力位U展开成球谐函数的形式[9-10]:
式中:GM表示火星的引力常数,R表示火星赤道的平均半径(3 396 km)(表 1);Pn,nm表示正则化的连带勒让德(Legendre)函数;(Cn,nm,Sn,nm)表示重力场正则化的n阶m次球谐展开系数,最大展开阶数为N;(r,θ,λ)表示研究点在火星球固坐标系中的坐标,其中r,θ,λ分别表示研究点的半径、经度和余纬度,n,m分别表示火星重力场模型展开的阶和次;N表示重力场模型的最大展开阶数.
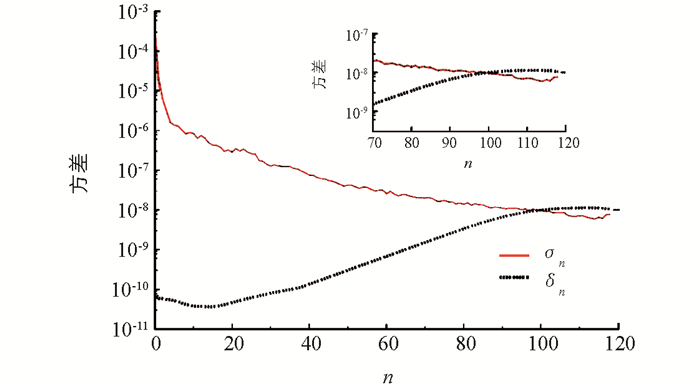
描述火星重力场基本特征的一个重要参数是重力场位系数的阶方差,即功率谱σn,它表征了重力场信号的强弱程度;而重力场模型位系数误差阶方差δn则反映了重力场模型位系数误差的频谱强度,其表达式分别为[9-10]:
相关参数的物理意义与(1)式同.基于重力场模型MRO120D的重力场位系数阶方差(红色实线)和位系数误差阶方差(黑色虚线)见图 1.很显然,位系数阶方差随阶数的增大而减小,相应的误差阶方差总体上在不断地增大,这说明位高阶位系数的可靠性不断地减小,特别是在100阶时,位系数阶方差与其误差阶方差的量级一致,甚至在100阶后小于相应的误差阶方差.正如文献[5]所述,MRO120D高阶项位系数在火星南半球的有效阶次较大,而在北半球的有效阶次较小,总体上使得全球模型的位系数误差阶方差在100阶后增大,因此,本研究在模拟过程中取最该模型的前100阶次位系数进行仿真分析.
-
在实际运用中,为了直观地描述实际重力相对参考重力的偏差,通常求取(1)式的径向梯度,并将重力归算到参考球面,可得自由空气重力异常,它是影响火星探测器轨道的主要因素.参考半径为R的球体外,任意一点(r,θ,λ)自由空气重力异常的表达式为[9-10]:
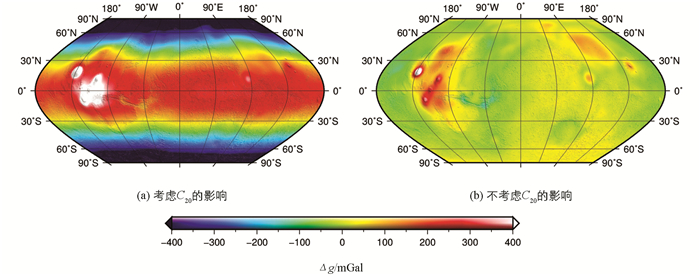
(3) 式中所有参数的意义与(1)式相同,这里取重力异常的单位为毫伽(1 mGal=1.0×10-5 m·s-2). 图 2表示220 km高度处(r=R+220 km)的自由空气重力异常分布,其中图 2(a)考虑了二阶位系数C20(为了方便,本文将“Cn,20”简述为“C20”)的影响,而图 2(b)没有考虑该系数的影响,二阶位系数C20通常表示天体扁率对重力异常的贡献,其大小见表 1. 图 2(a)明显地呈现出两极附近重力负异常,赤道附近重力正异常,图 2(b)则没有这种现象,这说明火星扁率对重力异常的贡献较大,或者说火星重力异常主要来自火星非球形扁率,它是火星探测器的主要摄动源.
-
为了分析重力场模型MRO120D对火星探测器轨道演化的影响,本研究采用动力学方法,利用重力场模型MRO120D的前100阶次位系数,运用美国宇航局NASA的定轨分析软件GEODYN Ⅱ[11]来进行仿真分析.在火星的球心坐标系中(惯性系),探测器环绕目标天体的运动方程可简写为
式中:右边第1项表示火星的中心引力,第2项表示本文考虑的各种摄动源,如火星非球形引力摄动,太阳、地球引力摄动,木星、水星、金星等大行星的引力摄动,火卫一Phobos和火卫二Deimos的引力摄动,基于火星大气模型DTM-Mars[8]的大气阻力摄动,太阳光压摄动,以及相对论效应等.由于各种摄动一般以球谐函数的形式进行表示,如公式(1)中火星表面引力位的球谐展开式,代入相关球谐展开系数即可计算探测器在不同位置时摄动力的大小.根据公式(1)和表 1中扁率位系数Cn,20及其他高阶位系数,即可计算火星探测器在不同位置时所受到的火星非球形引力摄动.同理,利用行星历表,也可以估计探测器在不同位置时所受其他天体的引力摄动,以及大气阻力摄动和太阳光压摄动等.由于引力与距离有关,一般地,火星的中心引力和非球形扁率摄动大于其他天体的引力摄动,但大气和太阳光压摄动效应也不能忽略[12].
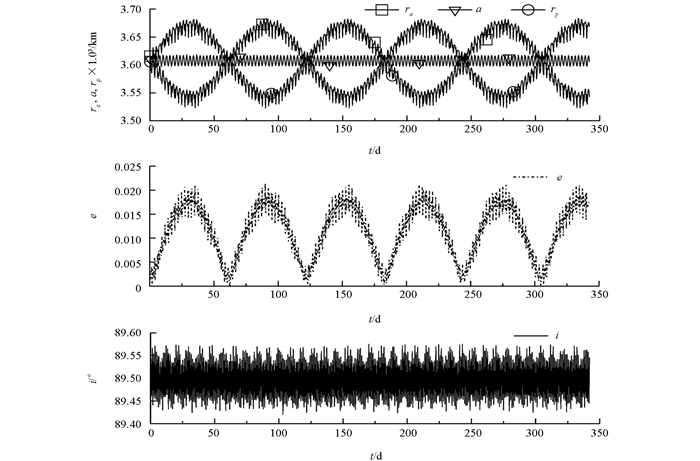
假设探测器处于贯穿火星南北极上空的圆轨道上,6个初始轨道根数中的5个初始值设置为:偏心率e0= 0.0,轨道面与赤道面夹角i0=89.5°,升交点赤经Ω0=0.0°,近月点幅角ω0=5.0°,平近点角M0=10.0°.参考以往火星探测器的轨道高度,假设探测器初始高度分别为h01=220 km,h02=150 km.由于初始轨道为圆轨道,可得两种高度对应的开普轨轨道根数半长轴的初始值a01=3546 km,a02=3626 km.初始历元为北京时间2021年1月2日8时0分0秒,轨道积分结束时间为2021年12月10日8时0分0秒.若计算过程中出现探测器近拱点距离小于火星平均半径rp<R时,则认为探测器因坠毁而停止运算.
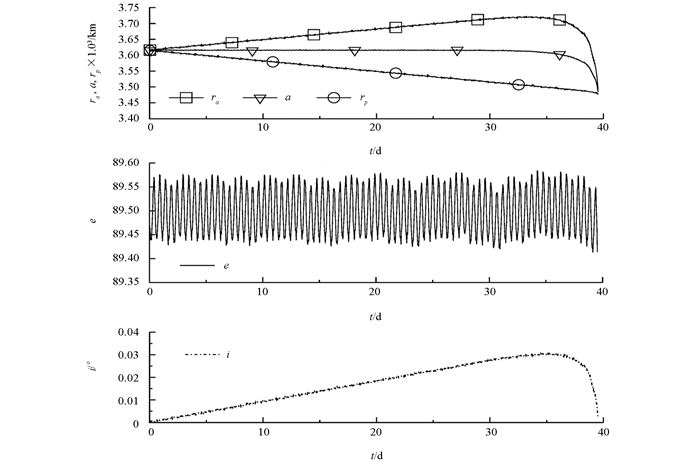
图 3表示探测器初始高度220 km时,基于重力场模型MRO120D,考虑二阶扁率摄动C20的探测器轨道根数的演化.很明显,远拱点ra、近拱点rp、偏心率e和轨道倾角i均出现长周期和短周期波动,半长轴a仅出现短周期变化.偏心率的长周期变化,表明探测器轨道在圆轨道与椭圆轨道之间交替变化.探测器在整个342 d的计算时间内正常运行,如果加长运行时间,探测器会仍然保持正常运行,由于篇幅所致,这里仅计算342 d的在轨时间.为了探究探测器长期变化的影响因素,图 4表示重力场模型MRO120D没有考虑二阶位系数C20的轨道演化.除偏心率e外,其它参数没有出现图 3那样的大幅度长周期变化,在轨运行时间也显著减小,总的运行时间不到40 d.这说明重力场模型的二阶位系数C20是稳定轨道的重要因素,也是产生长周期轨道变化的决定性参数.
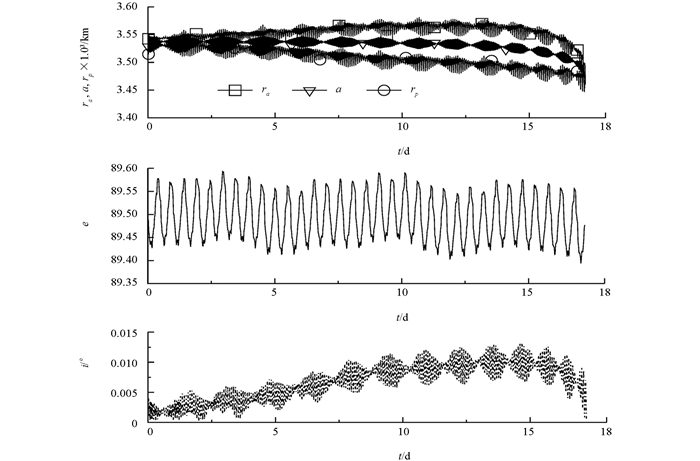
一般而言,探测器轨道越低,对重力场高阶短波长信号越敏感,有助于重力场模型高阶位系数的求解[5].为了进一步探究探测器保持正常运行的最低高度,图 5给出了初始高度为h02=150 km时,考虑重力场模型二阶位系数C20的轨道根数变化.受火星扁率的影响,轨道根数、近拱点和远拱点的球心距离出现了幅度较小的周期性变化.轨道高度越低,火星的大气阻力摄动越大[8],轨道稳定性越差,探测器总的运行时间不足18 d,这说明火星大气阻力效应非常明显.这也是早期火星着陆器成功率较低的原因,因为火星大气变化具有季节性的特点,并伴随一定的沙尘暴,易导致着陆器偏离正常轨迹而坠毁[13].受大气阻力的影响,发射150 km以下的低轨道探测器并不合适,综合而言,取初始轨道高度在220 km以上较能获得长的在轨时间.
-
深空探测是未来航天发展的重要方向,鉴于我国于2020年左右发射火星探测器,本研究利用动力学方法和最新的火星重力场模型MRO120D,考虑了火星中心引力及其非球形引力摄动,太阳、地球引力摄动,木星、水星、金星等大行星的引力摄动,火卫引力摄动和火星大气阻力摄动等,对初始轨道在220 km和150 km的探测器进行了仿真.结果表明探测器在220 km轨道高度处,考虑二阶项C20时能够在整个计算周期342 d内稳定地运行,且近拱点、远拱点、偏心率和轨道倾角均出现长周期波动.在相同初始高度下,不考虑C20时探测器在轨运行时间不足40 d,除偏心率e外,其它参数没有出现大幅度长周期变化,说明重力场模型位系数C20不仅是稳定轨道的重要因素,也是产生长周期轨道变化的决定性参数.受火星大气阻力的影响,探测器在150 km高度的在轨时间不足18 d,说明大气阻力效应对探测器的影响较大.为了获得较长的在轨时间,在满足相关科学任务的条件下,综合而言,我国即将发射的第一颗火星探测器,初始轨道设定在220 km以上是比较适宜的.



 下载:
下载: