-
动作识别是计算机视觉领域研究的热点问题,在人机交互、监控、体感游戏、智能家居等方面具有重要的实用价值[1].现如今,视频已成为人们生活中不可缺少的一种信息载体,随着视频呈现爆炸式地增加,如何迅速、准确地提取视频中人们所关注的内容,理解与识别图像序列中人体的动作意义重大[2-3].近年来,通过不断研究,产生了一些关于动作识别的算法.如杨顺卿等[4]提出了一种基于双语动态系统的行为识别方法,结合兴趣点检测与密集采样获取序列中的时空信息同时构建线性动态系统(LDS),然后对LDS进行编码;并利用LDS在码本中的分布与权重,通过动态系统袋(bag of dynamical systems,BODS)表征动作特征;接着通过K-SVD对得到的BODS特征操作,形成迁移字典对;最后通过OMP将字典在2个视角下进行动作的稀疏表示.该算法能够连续完整地表达图像序列,但是通过密集采样法会带来较多的冗余特征,导致计算效率低下.王鑫等[5]提出了一种利用流形学习的动作识别技术,该算法通过Kinect的深度内容获取活动位置,并利用相对活动位移差来得到运动特征;同时,借助Lalpacian映射流形对多维信号降维,得到了低维运动信息,在匹配过程中,通过改进的Hausdorff对低维空间样本和训练数据的进行相似测量,实验显示该算法识别效果良好.但是,此技术对视频中的视觉变化、相互遮挡等较为敏感. Davis等[6]提出了一种基于运动能量图的动作识别方案,首先,通过马氏距离获取模板间的距离,然后,根据观测与训练间的距离,引入了k-近邻完成对动作学习.该方法计算简单,但在选择时间间隔时不好确定.当间隔小,样本与训练的差别较小时,动作识别精度良好;相反,识别率不高,一般适用于简单动作识别.
为了降低动作识别中的特征冗余,提高识别精度和计算效率,本文提出了一种基于最大相关-最小冗余(MCMR)的动作识别方案.首先,在距离估计之前,使用SAX将时间序列转换为较短的符号序列,消除噪声影响的同时加快计算,并利用一个符号表示快速DTW测量.由于不同传感器种类与不同维度数据上动作的识别具有差异性,本文采用MCMR策略来选择合适的候选特征;然后,根据选择的特征,利用k-近邻分类学习;最后,对所提动作识别技术进行测试.
全文HTML
-
动态时间归整(DTW)能够解决优化问题,利用时间规整函数W(n)表示测试模板与参考模板的时序关联,以获取2个模板匹配的最小累加距离所对应的规整方程[7].
设2个时序Q,C,对应的长度为n,m,则
时序Q,C的距离设为D,表示为
如果n=m,直接计算时序Q,C的距离;如果n≠m,需要进行对齐操作.而线性缩放是将短时序伸长到与长时序相同的长度,或把长时序缩短使其与短时序长度相等,然后进行比较.
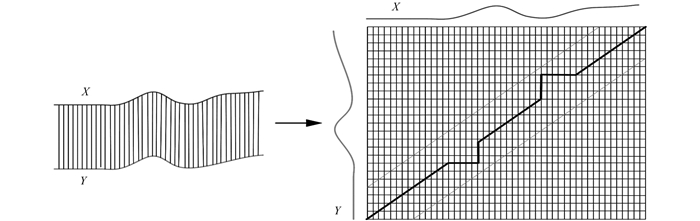
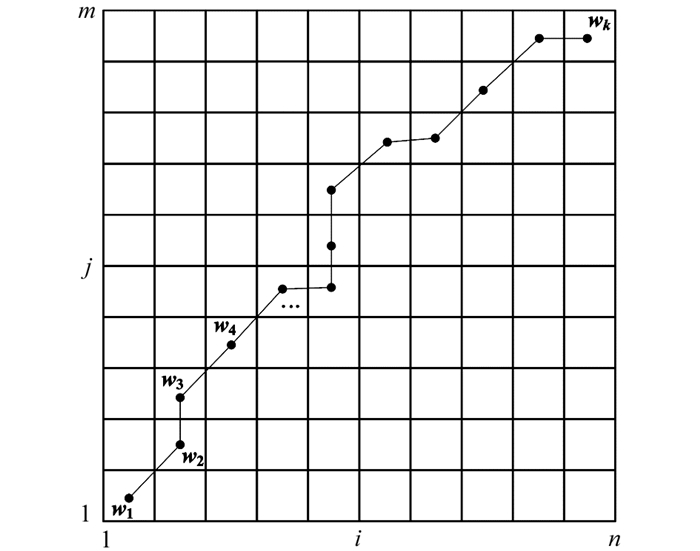
为了对齐时序Q,C,根据Q与C的距离,建立一个矩阵网格.矩阵中的单元为qi与cj的距离d(qi,cj),d(qi,cj)越小,相似性越高.为了得到一条通过网格中不同点的路线,使其经过的点为2个时序的对齐点.如图 1所示.
在本文算法中,把要寻找的这条路线定义为规整路线W.为了寻找一条最好的W,来建立Q,C的映射,令
其中,wk=(i,j)k为其第k单元.
W需满足以下几个条件:
1) 边界条件:w1=(1,1),wk=(n,m);
2) 连续性:设wk-1=(a′,b′),那么下个点wk=(a,b)符合(a-a′)≤1,(b-b′)≤1,表示无法越过某点来匹配,只允许与自己相邻点对齐.确保Q,C的所有坐标出现在W中;
3) 单调性:对于wk-1=(a′,b′),下一个点wk=(a,b),需符合0≤(a-a′),0≤(b-b′).从而确保W中的点可以随着时间单调完成.
通过连续性与单调性约束,每个点的路线就只有3个方向,如果路线通过了点(i,j),下个点可能为(i+1,j),(i,j+1),(i+1,j+1)这3个点中的一个.
为了获得感兴趣的点,通过W(n)计算规整成本最优的路线:
通过将2个时序进行缩放,可以获得2个时序的最短距离.在此,需选择一个路线,使最终总距离最优.为此,本文通过一个累加距离,将网格中所有点的距离进行相加,形成最后的总距离,因此,需要计算时序Q,C的相似度,计算公式如下所示:
最后,通过动态规划(dynamic programming)算法计算得到沿路线的累加距离,此距离为最小值,这条路线为最优路线.
-
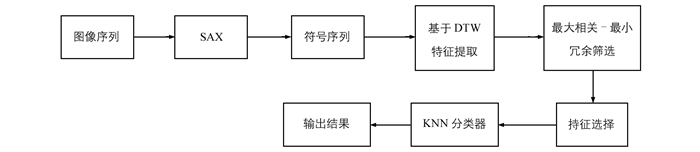
为了提高各种复杂动作的识别精度,将每一个运动传感器的数据定义成不可重复的多元时间序列片段,对于这种数据,通常采用基于距离相似的方法来处理.但是,由于传感器种类的多样性和匹配效率存在多维性,识别难度大,通常采用Shapelet变换来提高时间序列的识别敏感性[5].然而,该方法存在数据维度高、时间消耗大的问题.为此,本文设计了一个基于符号表示的快速DTW测量方法,在距离估计之前,使用SAX将原来的时间序列转化为较短的符号序列,以消除噪声影响,提高计算效率.因为传感器种类不同,在不同维度数据上动作的识别具有差异性,所以,采用基于最大相关-最小冗余的策略来选择最佳的候选特征,再根据选择的特征,利用k-近邻分类学习.算法流程图见图 2.
基于距离度量的运动时间序列识别方法是将时间序列之间的距离作为一种相似性度量,此方法在很多情况下都是有效的,如测试样本和选定的图案之间的神经网络嵌入距离与相似性测量方面.本文采用了测试运动系列与不同分类特征值序列之间的距离,并将其应用于不同种类的分类学习中.但是,由于存在不同人体执行的相同动作或者同一人执行不同动作的情况,因此,本文采用DTW方法进行距离估计.同时,考虑到时间成本,通过符号表示来降低数据维度.
-
设s={s1,s2,…,sn}为多维时间序列,表示一个单一的运动与维度传感器数据. si={sd1,sd2,…,sdm}为第i维度下长度为m的数据.由于动作范围存在差异,相似形状的相同运动也可能存在不同,因此,需要对数据标准化,以消除这种分歧.对于第i维的时间序列si,其标准化表示为:
其中,μsi为均值;σsi为标准差,分别定义如下:
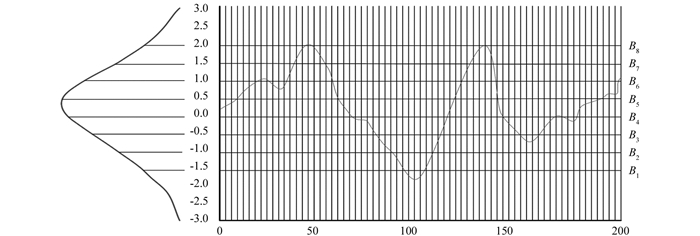
为了消除噪声影响的同时减少时间消耗,利用SAX将连续时间序列转换为离散符号序列[8].通过分段聚集近似(Piecewise Aggregate Approximation,PAA)技术,将时间序列划分成相同大小的片段.在相同概率的高斯分布下,断点B(B1,B2,…,Bp)将数据范围划分为p+1段,并将所有的片段转化为用相应的符号表示.对于一个时间序列si,设断点数为p,片段数为f,可得到一个符号序列sti{sti1,sti2,…,stif},f<m,对于sti中的每个元素,满足stif∈O1,O2,…,Op+1,1≤j≤f,O为一种符号的表示.操作过程见图 3.
通过上述过程,能够完成尺寸缩减和离散化.由于时间序列的长度变化会影响比较结果,因此,本文利用SAX将不同长度的运动转换为相同长度的序列.
-
DTW是时间序列相似估计中一种有效的距离度量手段,利用SAX得到的欧氏距离作为离散符号数据的下限距离[9].假设2个符号序列stx{x1,x2,…,xi,…,xld},sty{y1,y2,…,yi,…,yld},它们的下限距离定义如下所示:
其中,mx,my分别为数据x,y的长度;low为数据维数,ψ(xi,yi)计算如下所示:
对于多维数据而言,传统的距离度量可提供简单和快速的相似度测量.但这些距离序列对应2个时间序列,不适用偏移和时间漂移的场合,因此,本文引入了DTW来解决此问题.同时,为了加快计算,本文利用Sakoe-Chiba自带限制的匹配范围[10].对于符号序列stx{x1,x2,…,xi,…,xld},sty{y1,y2,…,yi,…,yld},其距离计算如下所示:
其中,bw为带宽约束.
一般地,可利用Euclidean距离测量匹配过程中xi与yi之间的相似性,
其中,dim为数据点的维度;xik,yjk分别表示xi与yi的第k维数据.匹配过程如图 4所示.
对于三维时间序列,数据点在每个时间上是一个三维数据,通过不同维度的相互关系选择一次匹配或在每个维度上的匹配.这2种选择可以得到不同的结果,分别设为DTWD,DTWI.事实上,DTWI比DTWD具有更高的运动感知性.虽然,无法实现对DTWI的不同距离累加,但可作为特征候选之一,通过相互间的最小相关性寻找到最有效的候选特征.
-
提高动作识别的精度要从多方面来考虑,其中特征选择是最重要的一个方面. MCMR能够筛选出具有不同类别、相互独立的特征[11],其选择过程主要由2个阶段组成:第一阶段,利用特征选择算法ReliefF(RF)来评估每个特征的区分能力[12],根据特征与类别的关联性来计算特征的权值,权值小于阈值τ的特征将被删除,选择出具有强类别相关性的特征作为候选特征;第二阶段,判断候选特征之间的相关性,选择相关性低的特征,直到收集了足够数量的特征为止.
ReliefF算法适用于多类问题的特征选择,通过几次迭代可确定每个特征的权重.在每次迭代中,ReliefF算法均是从标号数据集随机选择一个样本R,并从相同类别中提取k个最近邻样本.随后,计算其特征权重:
ff函数定义如下:
其中,F是从不同类别的标记数据中选择的候选特征;w(Fi)为第i个候选特征的权重;Hj为第j次近邻采样;Mj(C)为类别C的第j次近邻遗漏;max(Fj)与min(Fj)为Fj的最大和最小值,p(C),p(R)分别为类别C、样本R的概率.
但是,在上述过程中,候选特征忽略了特征间的关联和冗余,在实际过程中,需要消除冗余的候选特征.因此,根据RF权值,对特征进行降序排列,消除小于阈值的特征.对于剩余的候选特征,检查其是否具有相关性,如果一个候选特征与所选择的其他特征有密切的关系,也要剔除该特征.否则,将其作为最终的选择特征,直到收集了足够数量的特征为止.
在以往的研究中,提出了各种用于估计特征冗余的方法,例如信息增益、互信息、相关系数[13]等.但是,冗余的候选特征通常有相同的类可分性,意味着它们的RF权重具有较高的线性相关性.因此,本文采用基于RF权值的Pearson相关系数来表示特征间的关联[14]:
其中,wa表示所选特征的RF权重矩阵; wb表示候选的RF权重矩阵;P(a,b)表示Pearson相关系数. Pearson相关系数主要用于计算2个变量间的线性相关程度,其值是在-1和1之间. 1表示呈正相关;0表示无相关性;-1表示呈负相关.如果这个相关系数高于阈值,那么淘汰该候选特征.
-
为了准确地完成动作识别,需要对所选择的特征进行分类学习.本文引入了k-近邻(KNN)技术[15]. KNN是一种简单的非参数学习算法,对给定的数据中,搜索其最靠近的k个临近点,临近点最多的种类为该样本类别. k-近邻在分类时,只需利用最近的几个类别来确定未知类别,通过少量的样本就可避免分类不平衡问题.
令特征为{a1(x),a2(x),…,an(x)},ai(x)为x的第i个特征值,则样本XM与XN的距离表示为
KNN的计算过程如下所示:
1) 对特征归一化处理;
2) 计算已知点和求解点的距离;
3) 按照距离递增规律进行排列;
4) 选择与当前点距离最近的k个点;
5) 计算前k个点的概率;
6) 对前k个点中概率最大的特征进行类别召回,并判断为类别对象.
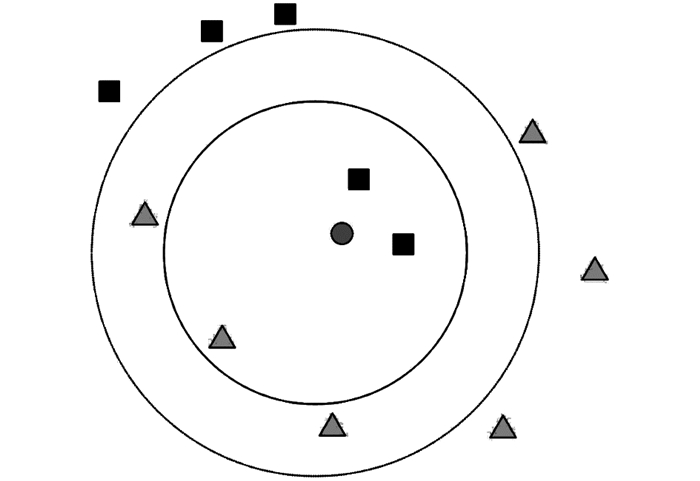
图 5显示了KNN分类操作.为了对未知的圆分类,令样本k=3,通过分析计算,圆和正方形接近数量高于三角形.因此,判定圆为正方形类别的.
基于近邻加权的KNN能够很好地降低噪声干扰,提高鲁棒性,并且计算精度高、对异常值不敏感.
2.1. 符号表示
2.2. 基于DTW的特征提取
2.3. 基于最大相关最小冗余筛选的特征选择
2.4. 分类器学习
-
为了验证所提动作识别算法的有效性,借助Kinect与IXMAS数据集来评价算法的性能.开发工具:Linux系统,QTCreator+OpenCV.测试条件为:CoreI 3,3.30GHz CPU,8GB运行RAM.为体现算法的有效性与先进性,将本文算法与文献[4]算法、文献[5]算法和文献[6]算法进行比较.经过多次试验,参数设定如下:断点数为p=5,η=0.5,数据维度为50,k-近邻分类器中k=8.本文采用的数据集与方法见表 1所示.
-
Kinect数据集是通过Kinect设备拍摄所形成的,通过10个对象在10种不同动作下重复2次从而形成了200个序列的运动集. Kinect数据集[16]中的动作包括走路、坐下、站起来、拿起、搬运、投掷、推、拉、挥舞、拍手,见图 6.数据集提供深度和骨架信息,对于这个数据集,遵循了跨学科的测试设置. IXMAS数据集[17]含有11种动作,每个动作分别由12个人执行3次,并且从5个不同方向进行拍摄,从而形成的一个多视角的数据集. 11种动作包括:Check watch,cross arms,get up,kick,pick up,punch,scratch head,sit down,turn around,walk,wave.该数据集包含了手臂、腿、躯干等相关部位中较全面的动作类型,具有较强的说服力.
-
表 2显示了本文算法在Kinect数据集中的混淆矩阵.根据表中的测量结果可知,本文算法在Kinect数据集中具有优异的识别能力,对各动作的识别率较高,能够对大多数动作进行准确识别.如“站起来”、“投掷”、“挥舞”等动作的识别率高达1.但有个别行动识别效果不太理想,如“走”、“推”动作识别率只有0.85,“走”易被作为“搬运”动作,“推”易被误认为“投掷”动作.主要是因为这些动作具有较多的相似性,导致其不能有效区分其提取的动作特征.
表 3为本文算法在IXMAS数据集中得到的混淆矩阵.从表 3中可看出,本文算法在IXMAS数据集中的识别精度较为理想,对各动作的识别率较高,能够对大多数动作进行准确识别.如“kick”,“scratch head”,“walk ”等动作的识别率高达1.但有个别行动识别效果不太理想,如“pick up”动作识别率只有0.80,“sit down”动作识别率只有0.85.因为“pick up”易被误认为“get up”、“sit down”动作,“sit down”易被误认为“get up”、“pick up”动作,这些动作具有较多的相似性,区别起来难度较大.
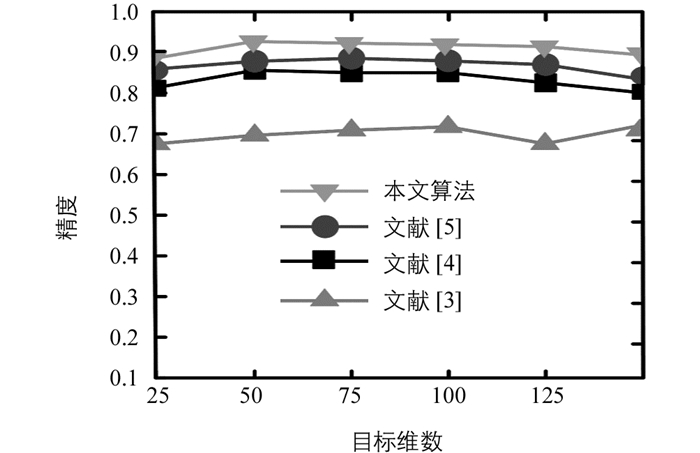
为了获得最优的性能,降低算法的复杂度,在不同的离散分割目标维数下测量算法的识别精度,结果见图 7.从图 7中可知,在目标维数为50时本文算法的识别性能最优.
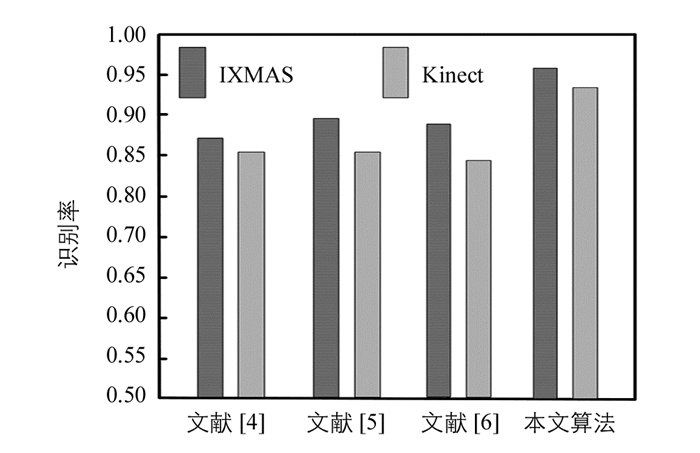
在Kinect与IXMAS数据集中,测试了3个对照算法以及本文算法的平均识别精度,如图 8所示.依据图 8可知,相对对照算法,本文算法在Kinect与IXMAS数据集中的识别率取得了优异的成绩,在Kinect与IXMAS中的平均识别率分别为96.23%,93.36%,与对照组算法相比有一定的提高.主要是因为本文利用SAX技术将连续的图像序列转换为离散符号序列,消除噪声影响的同时也减少了时间消耗;同时引入DTW计算符号序列的距离,提取时间序列的特征,解决时间漂移问题;然后,定义了一个RF特征权重,根据权重对特征进行降序排列,消除相关性弱的冗余特征,筛选出具有高相关性和低冗余的特征;最后,为了完成动作识别,根据筛选出的特征进行分类器学习,降低噪声干扰,提高了算法鲁棒性.而文献[4]是通过密集采样得到特征数据的,容易带来较多的冗余特征;文献[5]是基于位移差来得到运动特征的,容易受视频中的视觉变化、相互遮挡等动作的影响,识别效果不好;文献[6]在选择时间间隔时不好确定,一般用于简单动作识别中.
为了更全面检测算法的性能,对算法的运行时间进行测试,结果见表 4.根据表 4可知,本文算法在Kinect与IXMAS数据集中的平均运行时间为31.25 s,51.64 s,均低于文中的对照组算法,这表明本文算法具有较高的运算速度.其主要原因是本文利用了SAX方法将连续的图像序列转换为较短的离散符号序列,同时通过MCMR策略来选择合适的候选特征,消除冗余特征,有效地提高了算法效率.
3.1. 数据集
3.2. 实验结果
-
为了提高动作的识别精度与鲁棒性,降低冗余特征,提高算法效率,本文提出了一种基于最大相关-最小冗余的动作识别算法.为了消除噪声影响并提高算法的效率,在距离估计之前,通过使用SAX技术将原来的时间序列转换为较短的符号序列;采用DTW准确提取图像时间序列中的特征,避免了时间漂移;针对动作特征的相似性和差异性,采用了MCMR策略来选择合适的候选特征,MCMR根据特征权重对特征进行降序排列,消除弱相关性特征,选择高相关与低冗余特征;再根据选择的特征,利用k-近邻分类学习.实验证明了本文算法具有优异的识别率,降低了冗余特征,并有效地改善了算法的识别效率.本文的不足之处在于只在2个数据集上进行了实验,未来将着眼于处理更多的数据集,还将研究基于深度神经网络的人体动作识别.



 下载:
下载: