Uniqueness of Solutions of Maxwell's Equations in the Presence of Defects with Small Measurement

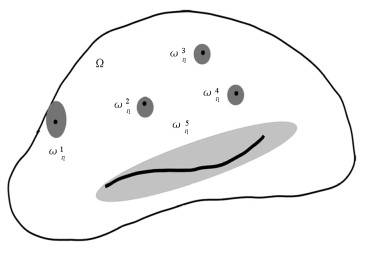
假定ω_ηⁱ⊂Ω为具有较小Lebesgue测度的可测子集.每一个小区域ω_ηⁱ包含一个缺陷，每个点缺陷和线缺陷(图中区域内的点和曲线段)分别由一个具有规则形状的较小区域所覆盖，且每个小区域ω_ηⁱ可以与边界∂Ω有交集(如图 1所示).令${\omega _\eta } = \bigcup\limits_{i = 1}^n {\omega _\eta ^i}, \quad \left| {{\omega _\eta }} \right|$表示ω_η的测度.

Maxwell方程的正散射问题解的唯一性可以描述成，在给定Silver-Muller散射条件的前提下证明方程系数满足相应正则性条件时解的唯一性，其中：有界区域Ω的外部由于方程系数转化成为常数，其唯一性可以通过Rellich引理进行证明(参见文献[6-8]中对方程的介绍及对引理的详细证明)；区域内部当方程系数为逐段W^1，∞时，在文献[1]中给予了唯一性证明.因此本文主要研究方程系数ε^-1(x)在无缺陷区域Ω\ω_η内逐段W^1，∞且ε^-1(x)在ω_η内为L^∞时Maxwell方程解的唯一性，即在背景问题的唯一性已初步解决的条件下讨论背景区域上增加小测度缺陷时的唯一性.更多关于小测度缺陷方面的研究，请查阅文献[9-13].为了讨论的方便，令R＞0为足够大的常数，B_R为半径R的一个开球且确保Ω⊂${B_{\frac{R}{2}}}$；定义如下两个索伯列夫空间X_T(B_R)和X_N(B_R)，

定理1  假设开集B_R\ω_η存在唯一一个连通分量，且在B_R\ω_η内ε^-1(x)为逐段W^1，∞的实对称正定矩阵.若k为给定的实常数，B_R为u∈X_T(B_R)∪X_N(B_R)的紧支撑且u为如下方程的弱解

则当|ω_η|足够小时，u在B_R内恒等于零.

证  由于B_R\ω_η为开集且只有一个连通分量，在此区域内ε^-1(x)为逐段W^1，∞或光滑的实对称正定矩阵，因此由文献[1]中的结论得知在区域B_R\ω_η内u≡0.

当u分别属于X_T(B_R)和X_N(B_R)时，(k²，u)为如下两种问题的特征解：

1) 当u_η∈X_T(B_R)时对应特征值和特征向量记为(λ_η^D，u_η)，满足如下方程

2) 当v_η∈X_N(B_R)时对应特征值和特征向量记为(λ_η^N，v_η)，满足如下方程

其中

当|ω_η|→0时，方程(2)趋向如下Dirichlet特征值问题

且方程(3)趋向如下Neumann特征值问题

在文献[9]中已给出，方程(2)的离散谱σ_η^D收敛于方程(4)的离散谱σ₀^D；类似的方程(3)的离散谱σ_η^N收敛于方程(5)的离散谱σ₀^N，而方程(4)和方程(5)不存在共同的特征值，由此我们将会通过下述推导获得定理1所述的结论.定义集合d_DN如下：

其中：λ^D∈σ₀^D，λ^D＜k²+1；λ^N∈σ₀^N，λ^N＜k²+1.

则d_DN＞0且存在δ＞0使得在|ω_η|＜δ内，

若u=u_η=v_η不恒等于零时，因k²∈σ^D∩σ_η^N，满足

矛盾产生，因此假设错误，原命题成立.

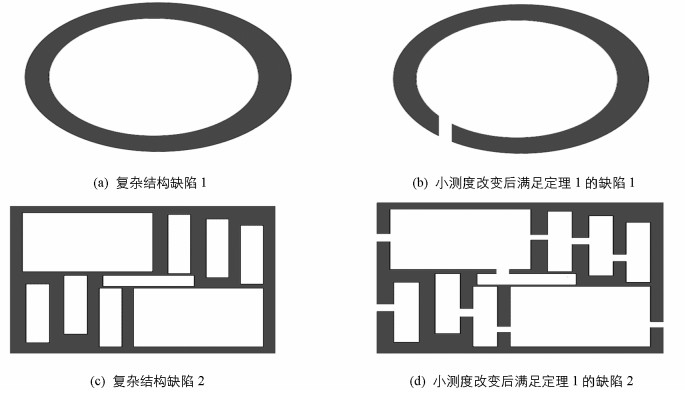
定理1中所述的缺陷Ω_D可以包含有限个满足定理1条件的缺陷而非局限于一个缺陷情况，然而定理1的结论只适用于缺陷之外的区域必须连通的情况，即B_R\ω_η存在唯一连通分量.因此下面将定理1结论延伸至B_R\ω_η为不连通的情况，比如存在封闭线缺陷的情况.其中主要的思想是对目标缺陷ω_η进行小测度的任意改变，并且确保改变后的缺陷${\widetilde \omega _\eta }$满足定理1的条件.在这种情况下所讨论的缺陷可以为带状，环状或者球状等具有复杂结构的缺陷(图 2).

推论1  对缺陷的区域ω_η进行任意改变，且改变后的缺陷${\widetilde \omega _\eta }$满足定理1的条件.当这些改变使得ω_η的测度发生微小变化时，定理1的结论仍成立，即u在B_R区域内恒等于零.

证  对于给定的ω_η进行小测度的任意改变，并且确保改变后的缺陷${\widetilde \omega _\eta }$满足定理1的条件.此时方程(1)在Ω上对应Neumann边值问题的离散谱$\tilde \sigma _\eta ^N$在Ω上收敛于σ_η^N；同理在新区域${\widetilde \omega _\eta }$上，方程(1)在Ω上对应Dirichlet边值问题的离散谱$\tilde \sigma _\eta ^D$在Ω上收敛于σ_η^D.另外对于η足够小时，在两个谱之间距离至少$\frac{1}{3}{d_{DN}}$时，$\tilde \sigma _\eta ^N$和$\tilde \sigma _\eta ^D$不存在小于1+k²的共同特征值，因此对目标缺陷进行适当的微小扰动可获得推论所述结论.