Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2020 Volume 42 Issue 12
Article Contents
Previous Article Next Article

PAN Yun, ZHAO Yuan-yao. The Effect of Working Memory Resource Wastage on Mental Arithmetic Processing[J]. Journal of Southwest University Natural Science Edition, 2020, 42(12): 142-148. doi: 10.13718/j.cnki.xdzk.2020.12.018
Citation: PAN Yun, ZHAO Yuan-yao. The Effect of Working Memory Resource Wastage on Mental Arithmetic Processing[J]. Journal of Southwest University Natural Science Edition, 2020, 42(12): 142-148. doi: 10.13718/j.cnki.xdzk.2020.12.018
shu

The Effect of Working Memory Resource Wastage on Mental Arithmetic Processing

  • School ofPsychology, Guizhou Normal University, Guiyang 550025, China

More Information
  • Received Date: 28/09/2019
    Available Online: 20/12/2020

  • MSC: B842.3

  • Using the mental arithmetic and articulation dual-task paradigm of Vall e-Tourangeau et al., the subjects were asked to add mental arithmetic on the interactivity of different problem representations while articulating continuously, to explore the effects of the interactivity of different problem representations on working memory resource wastage and math anxiety in different calculation lengths. The results showed that under short computing conditions, the interactivity of different problem representations had a significant impact on the accuracy and calculation deviation, but had no significant impact on the calculation time and efficiency; that under long computing conditions, the interactivity of different problem representations had a significant impact on the accuracy, calculation deviation, calculation time and efficiency; and that under the condition of long computation and low interaction problem representation, there was a significant positive correlation between math anxiety and calculation deviation, and the higher the degree of math anxiety, the greater the calculation deviation. In conclusion, high interaction problem representation reduces the impact of working memory resource wastage on mental arithmetic results, the interactivity of problem representation plays a greater role in relatively complex arithmetic, and math anxiety is an important factor affecting mental arithmetic processing.
  • 加载中
  • [1] MACLELLAN E. Mental Calculation: Its Place in the Development of Numeracy[J]. Westminster Studies in Education, 2001, 24(2): 145-154.

    Google Scholar

    [2] GROEN G J, PARKMAN J M. A Chronometric Analysis of Simple Addition[J]. Psychological Review, 1972, 79(4): 329-343.

    Google Scholar

    [3] ASHCRAFT M H, BATTAGLIA J. Cognitive Arithmetic: Evidence for Retrieval and Decision Process in Mental Addition[J]. Journal of Experimental Psychology: Human Learning and Memory, 1978, 4(5): 527-538.

    Google Scholar

    [4] HITCH G J. The Role of Short-term Working Memory in Mental Arithmetic[J]. Cognitive Psychology, 1978, 10(3): 302-323.

    Google Scholar

    [5] ADAMS J W, HITCH G J. Working Memory and Children's Mental Addition[J]. Journal of Experimental Child Psychology, 1997, 67(1): 21-38.

    Google Scholar

    [6] LOGIE R H, GILHOOLY K J, WYNN V. Counting on Working Memory in Arithmetic Problem Solving[J]. Memory & Cognition, 1994, 22(4): 395-410.

    Google Scholar

    [7] LEMAIRE P, ABDI H, FAYOL H. The Role of Working Memory Resources in Simple Cognitive Arithmetic[J]. European Journal of Cognitive Psychology, 1996, 8(1): 73-104.

    Google Scholar

    [8] VALLÉE-TOURANGEAU F, SIROTA M, VALLÉE-TOURANGEAU G. Interactivity Mitigates the Impact of Working Memory Depletion on Mental Arithmetic Performance[J]. Cognitive Research: Principles and Implications, 2016, 1(1): 1-8.

    Google Scholar

    [9] ROSS W, VALLÉE-TOURANGEAU F, HERWEGEN J V. Mental Arithmetic and Interactivity: the Effect of Manipulating External Number Representations on Older Children's Mental Arithmetic Success[J]. International Journal of Science and Mathematics Education, 2020, 18: 985-1000.

    Google Scholar

    [10] ALLEN M, VALLÉE-TOURANGEAU F. Interactivity Defuses the Impact of Mathematics Anxiety in Primary School Children[J]. International Journal of Science and Mathematics Education, 2016, 14(8): 1553-1566.

    Google Scholar

    [11] GUTHRIE L G, VALLÉE-TOURANGEAU F. Numbers in Action: Individual Differences and Interactivity in Mental Arithmetic[J]. Cognitive processing, 2018, 19(3): 317-326.

    Google Scholar

    [12] 刘效贞.不同情境状态下数学焦虑对估算的影响[D].济南: 山东师范大学, 2009.

    Google Scholar

    [13] VALLÉE-TOURANGEAU F, SIROTA M, VILLEJOUBERT G. Reducing the Impact of Math Anxiety on Mental Arithmetic: the Importance of Distributed Cognition[C]. Proceedings of the Annual Meeting of the Cognitive Science Society, Austin, Cognitive Science Society, 2013: 3615-3620.

    Google Scholar

    [14] 刘昌, 王翠艳.心算的加工机制:来自认知神经科学的研究[J].心理科学进展, 2008, 16(3): 446-452.

    Google Scholar

    [15] 王翠艳, 刘昌.数学焦虑对心算加工的影响[J].心理科学进展, 2007, 15(5): 795-801.

    Google Scholar

    [16] ASHCRAFT M H, ELIZABETH P K. The Relationships Among Working Memory, Math Anxiety, and Performance[J]. Journal of Experimental Psychology: General, 2001, 130(2): 224-237.

    Google Scholar

    [17] 王银华, 徐展, 吕恒, 等.保持时间和存储负荷对工作记忆广度的影响[J].西南大学学报(自然科学版), 2009, 31(12): 156-160.

    Google Scholar

    [18] PAAS F, RENKL A, SWELLER J. Cognitive Load Theory and Instructional Design: Recent Developments[J]. Educational Psychologist, 2003, 38(1): 1-4.

    Google Scholar

    [19] 代曼, 刘儒德, 邸妙词, 等.工作记忆负荷和自动化提取对小学生加法心算策略执行效果的影响[J].心理发展与教育, 2014, 30(4): 420-426.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(2)  /  Tables(2)

Export Citation
PDF
XML

Article Metrics

Article views(668) PDF downloads(127) Cited by(0)

Access History

Other Articles By Authors

The Effect of Working Memory Resource Wastage on Mental Arithmetic Processing

  • Received Date: 28/09/2019
  • Available Online: 20/12/2020

Abstract: Using the mental arithmetic and articulation dual-task paradigm of Vall e-Tourangeau et al., the subjects were asked to add mental arithmetic on the interactivity of different problem representations while articulating continuously, to explore the effects of the interactivity of different problem representations on working memory resource wastage and math anxiety in different calculation lengths. The results showed that under short computing conditions, the interactivity of different problem representations had a significant impact on the accuracy and calculation deviation, but had no significant impact on the calculation time and efficiency; that under long computing conditions, the interactivity of different problem representations had a significant impact on the accuracy, calculation deviation, calculation time and efficiency; and that under the condition of long computation and low interaction problem representation, there was a significant positive correlation between math anxiety and calculation deviation, and the higher the degree of math anxiety, the greater the calculation deviation. In conclusion, high interaction problem representation reduces the impact of working memory resource wastage on mental arithmetic results, the interactivity of problem representation plays a greater role in relatively complex arithmetic, and math anxiety is an important factor affecting mental arithmetic processing.

    HTML

  • 心算是指在不借助外部工具情况下进行算术运算的过程[1]，是人们日常生活中的一种重要思维活动和技能.关于心算的机制主要有2种观点：一是计数理论[2]，认为加法的解答过程可分为问题编码、计算、决策和反应执行4个阶段，其中计算所需时间决定了总体反应时.二是提取理论[3]，认为个体在经过大量练习后已经记住了很多心算答案，因此在进行心算解答时，能够从记忆中直接提取答案，也可能偶尔会使用计算策略.

    有研究表明，工作记忆是影响心算加工的重要因素.如Hitch[4]的研究发现，心算中所发生的大量错误是因为被试没有把中间结果正确记录并保存到工作记忆中；Adams等[5]对7~11岁儿童心算与工作记忆广度关系的研究结果发现，心算加工所需要的时间与工作记忆广度存在显著负相关，表明工作记忆是影响儿童心算成绩的重要资源；Logie等[6]的实验结果发现干扰工作记忆的中央执行系统和语音环路会影响个体的心算成绩，说明工作记忆的中央执行系统和语音环路在心算过程中起着重要作用.此外，也有研究者探讨了工作记忆的发音抑制对心算成绩影响，如Lemaire等[7]在实验中要求被试以每两秒一个单词的速度复述“the”且对等式做真假判断，结果表明语音任务影响真等式(如，6+7=13)，但并不影响假等式(如，6+7=17)；Vallée-Tourangeau等[8]的研究要求被试连续发音“the”并在不同的问题表征交互条件下做加法心算，结果发现无论是在低交互还是高交互问题表征下，发音条件下的正确率和效率都低于不发音条件，说明高交互问题表征降低了由发音抑制引起的工作记忆资源损耗；Ross等[9]在实验中要求7~9岁儿童背诵字母表的同时对不同问题表征交互条件做加法心算，结果发现无论工作记忆负载如何，高交互条件下的正确率都更高，说明高交互问题表征和工作记忆在心算和数字认知模型中具有重要性.

    除工作记忆外，心算加工也受到计算长度和问题表征的影响.如Allen等[10]在实验中采用7和11个数字为材料，要求9~11岁儿童被试在不同交互性条件下做加法心算，结果发现高交互问题表征提高了心算的正确率和效率；Guthrie等[11]使用11和17个数字为材料，要求被试在不同交互性条件下做加法心算，结果发现高交互的问题表征提高了心算的正确率及效率，但缩小了高低数学焦虑个体的差异.这些结果表明在高交互的表征条件下个体可能会得出不同的问题解决方法，缺乏互动性的有限资源可能会限制个体问题解决的能力.

    综上，尽管已有研究探讨了问题表征交互性与计算长度对心算加工的影响[10-11]，也有研究考察了问题表征交互性与工作记忆发音抑制对心算的影响[8]，但目前尚未有研究探讨问题表征交互性、计算长度与工作记忆发音抑制对心算加工的影响.那么，问题表征交互性在更短的数字材料中是否会对工作记忆资源损耗产生影响呢？这是本研究所要探讨的问题.为此，本研究在Vallée-Tourangeau等[8]实验范式基础上，以5个和11个数字为材料，探讨不同计算长度条件下问题表征交互性对工作记忆资源损耗的影响.

1.   研究方法

    1.1.   研究对象

  • 选取贵州某高校被试83名，其中38名(女33名)参与短计算(5个数字)，平均年龄(19.68±1.58)岁；45名(女40名)参与长计算(11个数字)，平均年龄(20.29±2.08)岁.视力或矫正视力正常.

    • 1.2.   实验材料

    1.2.1.   心算材料

  • 分别有10组短计算(5个数字)和10组长计算(11个数字)，2个计算组中分别选取5组以A4纸(低交互)呈现，另外5组以数字令牌拼盘(高交互)呈现.实验前主试对短计算(5个数字)和长计算(11个数字)的计算正确率进行了差异检验，结果发现5个数字和11个数字的计算正确率差异有统计学意义，t(18)=4.40，p＜0.001.

    • 1.2.2.   数学焦虑量表

  • 采用刘效贞[12]2009年修订的修订数学焦虑量表，该量表共21题，采用Likert 5级评分法. “没有焦虑”得1分，“有点焦虑”得2分，“一般焦虑”得3分，“比较焦虑”得4分，“非常焦虑”得5分.该量表具有良好的结构效度和内部一致性信度，总体α系数为0.932.得分越高说明数学焦虑程度越高.

    • 1.3.   实验设计

  • 采用2(计算长度：短、长)×2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)三因素混合实验设计.其中计算长度为被试间变量，发音抑制和交互性为被试内变量.因变量为正确率、计算偏差、计算用时和效率.

    • 1.4.   实验程序

  • 向一组被试呈现短计算(5个数字)，另一组被试则呈现长计算(11个数字)，要求2组被试将所有呈现出来的数字做加法心算.实验过程中将会以2种形式来呈现：一种是以A4纸呈现即低交互，数字随机排列在纸上，要求被试双手平放于桌面，并且不允许用手指数或点A4纸上的数字；另一种是以数字令牌拼盘呈现即高交互，刻有1-9(5除外)数字的数字令牌随机排列在拼盘上，被试在计算过程中可以随意移动呈现出来的数字令牌.发音条件下要求被试连续重复发音“这”并做加法心算；不发音条件下仅做加法心算即可.在低交互问题表征下，当A4纸翻开时开始计时；在高交互问题表征下，拼盘盖上挡板，挡板移开时开始计时，被试报告计算结果后停止计时.

    4个条件中(低交互发音、高交互发音、低交互不发音、高交互不发音)具有相同交互性的条件不能连续出现(如，连续出现2个高交互条件).第一次呈现发音抑制之前需要进行一项训练任务，在这项任务中，要求被试连续重复发音“这”，同时做1 min的100连续减3，并完成数学焦虑量表.

2.   结果与分析

    2.1.   正确率

  • 对数据进行2(计算长度：短、长)×2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)的重复测量方差分析，结果发现，计算长度的主效应显著，F(1，81)=17.83，p＜0.001，η2=0.18；发音抑制的主效应显著，F(1，81)=39.49，p＜0.001，η2=0.33；交互性的主效应显著，F(1，81)=48.07，p＜0.001，η2=0.37.交互性与计算长度的交互作用显著，F(1，81)=10.72，p＜0.01，η2=0.12.简单效应分析表明：短计算条件下，高交互的正确率(88.9%)比低交互的正确率(82.9%)更高，F(1，81)=6.17，p＜0.01，η2=0.07；长计算条件下，高交互的正确率(81.6%)比低交互的正确率(64.7%)更高，F(1，81)=56.89，p＜0.001，η2=0.41.

    分别对不同计算长度的数据进行分析(表 1)，发现短计算(5个数字)的心算在不发音且高交互条件下正确率最高. 2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)重复测量方差分析发现，发音抑制的主效应显著，F(1，37)=9.73，p＜0.01，η2=0.21；交互性的主效应显著，F(1，37)=11.43，p＜0.01，η2=0.24；发音抑制与交互性的交互作用不显著，F(1，37)=1.39，p＞0.05，η2=0.04.

    长计算(11个数字)的心算在不发音且高交互条件下正确率最高.重复测量方差分析发现，发音抑制的主效应显著，F(1，44)=33.39，p＜0.001，η2=0.43；交互性的主效应显著，F(1，44)=41.03，p＜0.001，η2=0.48；发音抑制与交互性的交互作用显著，F(1，44)=6.31，p＜0.05，η2=0.48.简单效应分析表明：发音条件下，高交互的正确率(77.3%)高于低交互的正确率(55.1%)，F(1，44)=32.84，p＜0.001，η2=0.43；不发音条件下，高交互的正确率(85.8%)高于低交互的正确率(74.2%)，F(1，44)=16.96，p＜0.001，η2=0.28.

    • 2.2.   计算偏差

  • 对数据进行2(计算长度：短、长)×2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)的重复测量方差分析，结果发现，计算长度的主效应显著，F(1，81)=19.84，p＜0.001，η2=0.20；发音抑制的主效应显著，F(1，81)=21.45，p＜0.001，η2=0.21；交互性的主效应显著，F(1，81)=27.68，p＜0.001，η2=0.26.交互性与计算长度的交互作用不显著，F(1，81)=3.71，p＞0.05，η2=0.04.

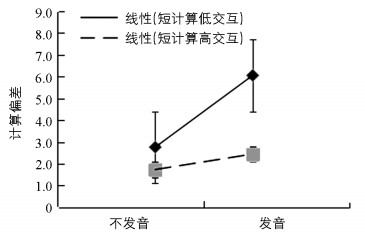
    分别对不同计算长度的数据进行分析(图 1)，结果发现，短计算(5个数字)的计算偏差在高交互条件下相较于低交互条件下较小. 2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)重复测量方差分析发现，发音抑制的主效应显著，F(1，37)=7.77，p＜0.01，η2=0.17；交互性的主效应显著，F(1，37)=8.36，p＜0.01，η2=0.18；发音抑制与交互性的交互作用显著，F(1，37)=5.15，p＜0.05，η2=0.12.简单效应分析表明：发音条件下，高交互的计算偏差(2.45)小于低交互的计算偏差(6.05)，F(1，37)=9.01，p＜0.01，η2=0.20；不发音条件下，高交互的计算偏差(1.74)与低交互的计算偏差(2.76)差异无统计学意义，F(1，37)=2.17，p＞0.05，η2=0.06.

    如图 2所示，长计算(11个数字)的计算偏差在高交互条件下相对于低交互条件下较小.重复测量方差分析发现，发音抑制的主效应显著，F(1，44)=15.71，p＜0.001，η2=0.26；交互性的主效应显著，F(1，44)=21.28，p＜0.001，η2=0.33；发音抑制与交互性的交互作用显著，F(1，44)=7.42，p＜0.01，η2=0.14.简单效应分析表明：发音条件下，高交互的计算偏差(6.62)小于低交互的计算偏差(14.20)，F(1，44)=22.40，p＜0.001，η2=0.34；不发音条件下，高交互的计算偏差(4.62)与低交互的计算偏差(7.02)差异无统计学意义，F(1，37)=3.64，p＞0.05，η2=0.08.

    • 2.3.   计算用时

  • 对数据进行2(计算长度：短、长)×2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)的重复测量方差分析，结果发现，计算长度的主效应显著，F(1，81)=146.51，p＜0.001，η2=0.64；发音抑制的主效应显著，F(1，81)=45.94，p＜0.001，η2=0.36；交互性的主效应显著，F(1，81)=27.41，p＜0.001，η2=0.25；交互性与计算长度的交互作用显著，F(1，81)=26.48，p＜0.001，η2=0.25.简单效应分析表明：短计算条件下，高交互的心算用时(7.74 s)与低交互的心算用时(7.69 s)差异无统计学意义，F(1，81)＜0.01，p＞0.05，η2＜0.001；长计算条件下，高交互的心算用时(25.40 s)比低交互的心算用时(19.82 s)更长，F(1，81)=58.53，p＜0.001，η2=0.42.

    分别对不同计算长度的数据进行分析，如表 1所示，短计算(5个数字)的计算用时在发音且高交互条件下最长. 2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)重复测量方差分析发现，发音抑制的主效应显著，F(1，37)=36.39，p＜0.001，η2=0.50；交互性的主效应不显著，F(1，37)=0.01，p＞0.05，η2＜0.001；发音抑制与交互性的交互作用不显著，F(1，37)=0.01，p＞0.05，η2＜0.001.>

    长计算(11个数字)的计算用时在发音且高交互条件下最长.重复测量方差分析发现，发音抑制的主效应显著，F(1，44)=34.59，p＜0.001，η2=0.44；交互性的主效应显著，F(1，44)=36.39，p＜0.001，η2=0.45；发音抑制与交互性的交互作用显著，F(1，44)=6.53，p=0.014，η2=0.13.简单效应分析表明：发音条件下，高交互的心算用时(29.47 s)比低交互的心算用时(21.70 s)更长，F(1，44)=25.42，p＜0.001，η2=0.37；不发音条件下，高交互的心算用时(21.33 s)比低交互的心算用时(17.95 s)更长，F(1，44)=14.11，p＜0.01，η2=0.24.

    • 2.4.   效率

  • 对数据进行2(计算长度：短、长)×2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)的重复测量方差分析，结果发现：计算长度的主效应不显著，F(1，81)=0.89，p＞0.05，η2=0.01；发音抑制的主效应不显著，F(1，81)=1.88，p＞0.05，η2=0.02；交互性的主效应显著，F(1，81)=7.84，p＜0.01，η2=0.09.交互性与计算长度的交互作用显著，F(1，81)=7.80，p＜0.01，η2=0.09>，简单效应分析表明：短计算条件下，高交互的心算效率(1.39)和低交互的心算效率(1.39)相同，F(1，81)＜0.001，p＞0.05，η2＜0.001；长计算条件下，高交互的心算效率(1.42)比低交互的心算效率(1.16)更高，F(1，81)=17.08，p＜0.001，η2=0.17.

    分别对不同计算长度的数据进行分析(表 1)，发现短计算(5个数字)的效率无论是在发音条件还是不发音条件下均无显著差异. 2(发音抑制：发音、不发音)×2(交互性：低交互、高交互)重复测量方差分析发现，发音抑制的主效应不显著，F(1，37)=1.33，p＞0.05，η2=0.04；交互性的主效应不显著，F(1，37)＜0.001，p＞0.05，η2＜0.001；发音抑制与交互性的交互作用不显著，F(1，37)=2.11，p＞0.05，η2=0.05.

    长计算(11个数字)的效率在发音且高交互条件下最高.使用重复测量方差分析，结果发现：发音抑制的主效应显著，F(1，44)=8.11，p＜0.01，η2=0.16.交互性的主效应显著，F(1，44)=18.36，p＜0.001，η2=0.29.发音抑制与交互性的交互作用显著，F(1，44)=21.82，p＜0.001，η2=0.33.简单效应分析表明：发音条件下，高交互的心算效率(1.46)比低交互的效率(0.91)更高，F(1，44)=29.33，p＜0.001，η2=0.33；不发音条件下，高交互的心算效率(1.37)与低交互的效率(1.40)差异无统计学意义，F(1，44)=0.13，p＞0.05，η2＜0.01.

    • 2.5.   数学焦虑

  • 如表 2所示，在短计算(5个数字)任务中，数学焦虑的程度对计算偏差无影响；然而在长计算(11个数字)任务中，数学焦虑的程度越高计算偏差越大，r=0.37，p＜0.05，尤其在低交互问题表征下，计算偏差受数学焦虑的影响较大，r=0.40，p＜0.01.

3.   讨论

  • 本研究发现，长计算条件下低交互的正确率相较于高交互时下降了16.9%，计算用时减少了5.58 s；短计算条件下低交互的正确率相较于高交互时下降了6%，计算用时差异无统计学意义，表明在长计算条件下问题表征交互性对心算的影响会更大，这与已有研究结果相似[10, 13].分析其原因可能是11个数字复杂程度更高，在计算时会涉及更多的步骤和进位，这些因素增加了工作记忆资源的损耗和计算错误的可能性，在高交互问题表征下，个体通过对数字令牌进行重构得出不同的算法策略，这些策略在低交互问题表征下很难从长时记忆中检索出来[10].

    本研究发现在短计算任务中，问题表征交互性对心算的正确率和计算偏差有显著的影响，但对计算用时和效率无显著影响，这与已有研究结果相似[11]，说明计算用时和效率不受问题表征交互性的影响.分析其原因可能是5个数字的计算过于简单，个体在计算时可直接从长时记忆中提取部分结果，而不像复杂算术那样需要进位、存储中间值等过程[14].同时，计算偏差与数学焦虑相关不显著，说明数学焦虑不会对简单的心算问题产生影响.这可能是因为焦虑情绪主要占用中央执行系统和语音环路的资源，当认知加工任务过多占用中央执行系统或语音环路资源时，焦虑会更明显.因此，焦虑对认知活动的影响是建立在一定任务难度水平上的，一些基本不需要工作记忆资源的、简单的心算问题是不会产生数学焦虑的[15].

    本研究还发现在长计算任务中的高交互问题表征下，发音抑制的正确率相较于不发音时下降了8.5%，计算用时增加了8.14 s；低交互问题表征下，发音抑制正确率相较于不发音时下降了19.1%，计算用时增加了3.75 s.说明在计算过程中对问题进行重构能够减少工作记忆资源的损耗.这是因为在低交互问题表征下任务很难进行，与此同时还受发音抑制的影响，从而导致个体在低交互问题表征下比在高交互下更快放弃了计算，且更容易猜测答案[8].此外，计算偏差与数学焦虑呈显著的正相关，尤其是在低交互问题表征下，数学焦虑程度越高计算偏差越大，但在高交互问题表征下未出现相关性，说明在低交互问题表征下，发音抑制增加了工作记忆资源的损耗，而高交互问题表征更具有灵活性[8].分析其原因可能是，在低交互问题表征下，随着数学焦虑程度的增加，使本该用于数学运算的工作记忆容量减少，从而导致心算结果相较于高交互问题表征时较差[16]，高交互问题表征增强了个体与外部环境的互动，降低了工作记忆资源的损耗[10].

    个体在进行复杂心算时，尽管每一步计算都是从长时记忆中提取先前熟练的计算结果，但由于步骤较多，个体需要在工作记忆中做大量的认知操作，如从长时记忆中提取算术结果，保存中间值、进位等[14]，又如由于资源有限，复杂的活动没有足够的认知资源[17]，因此工作记忆的负荷较大，导致心算成绩较低.根据认知负荷理论[18]，认知负荷是指针对某一特定认知任务、工作记忆系统对其相关信息进行储存与加工过程中所承受的负荷总量.工作记忆加工信息的方式有2种：一是有意识加工；二是自动化加工.有意识的加工会占用工作记忆许多资源，而自动化加工基本上不受意识监控，占用极少的工作记忆资源[19].

Figure (2)  Table (2) Reference (19)

Catalog

    Copyright Journal of Southwest University Natural Science Edition

    Address： Tel：023-68254576, 68252540, 68366165,68366917 E-mail：lkxb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return