Optimal Investment Portfolio-Cheap Reinsurance-Threshold Dividend Strategies under Compound Poisson-Geometric Risk Process

文章所假设的随机过程和随机变量都定义在完备概率空间(Ω，F，F_t，P)上，产生的σ-域流{F_t：t＞0}完备且右连续. 允许连续交易且资产可任意分割，无摩擦、自融资且无套利.

本节先给出赔付过程、盈余过程、财富过程和阈值分红策略的数学描述，最后再给出保险公司的最优控制问题.

文献[1-2]分别提出了复合Poisson-Geometric分布与过程. 关于复合Poisson-Geometric分布的定义也可参考文献[16]，下面只给出复合Poisson-Geometric过程的定义.

定义1^[2]  设λ＞0，0≤γ＜1，称随机过程{N(t)}是服从参数λ，γ的复合Poisson-Geometric过程，如果满足

1) N(0)=0;

2) N(t)具有独立平稳增量;

3) 对任意t≥0，N(t)服从参数为λ，γ的复合Poisson-Geometric分布，且

注1  当γ=0时，复合Poisson-Geometric过程退化为一般的Poisson过程，常称γ为偏离系数.

设$S(t)=\sum\limits_{i=1}^{N_{1}(t)} Y_{i}$表示到时刻t为止的累积赔付额，其中：Y_i表示第i次支赔时的赔付额，N₁(t)为服从参数是λ，γ的复合Poisson-Geometric过程，表示到时刻t为止发生赔付的次数，偏离系数γ表示了赔付过程因免赔而被稀疏的程度.

复合Poisson-Geometric风险(简称复合P-G风险)下，Cramer-Ludberg盈余模型被推广为

其中：x表示初始盈余，c表示保费率，S(t)表示到时刻t为止的累积赔付.

假设Y_i服从参数为$\frac{1}{m}$的指数分布，则由文献[2]的引理4，可知

其中p₁=E[Y_i]=m，p₂=E[Y_i²]=2m². 根据文献[19]的研究，经典的盈余过程(1)可近似地用扩散过程

来描述，其中B₁(t)是一维标准布朗运动. 假设{N(t)}，{B₁(t)}，{Y_i}相互独立. 为安全起见，保费率须满足$c=(1+\theta) \frac{\lambda m}{1-\gamma}$，θ＞0称为保险负载系数. 则盈余过程(2)可近似表示为扩散过程

在破产前，保险公司将部分财富π(t，x)投资到一个价格P(t)满足

的风险资产(比如股票)上. 这里μ₀是风险资产的单位风险资产的期望收益率，σ₀是单位风险资产的期望波动率，B₂(t)是一维标准布朗运动，设B₂(t)与B₁(t)的相关系数为ρ. 最后将剩余财富投资于价格P₀(t)满足

的无风险资产上，其中单位无风险资产的收益率为r₀(＜μ₀). 则财富过程X(t)满足

这里进一步考虑再保业务，并假设再保的自留比例(风险暴露)为q(t，x)，再保的负载系数为η(≥θ)，则财富过程可进一步表示为

也即

保险公司对股东或投保人按阈值分红策略进行红利分配. 设b＞0，当修正财富低于b时，不分红; 修正财富超过b时，将超出的部分按一个有界的比例l进行分红，其中0≤l≤α; 这种分红策略常被称为阈值分红.

设D(t)是时刻t的分红，则$\widetilde{X}(t)=X(t)-\bar{D}(t)$表示修正财富. 设$\tau=\inf \{t \geqslant 0 \mid \widetilde{X}(t) \leqslant 0\}$为保险公司的破产时刻，则对于t≤τ有$\bar{D}(t)=\int_{0}^{t} \alpha I_{\{\tilde{X}(s) \geqslant b\}} \mathrm{d} s$. 直到破产发生时，阈值分红的累积现值D=$\int_{0}^{\tau} \mathrm{e}^{-\delta t} \mathrm{~d} \bar{D}(t)$.

称满足

1) 0≤q(t，x)≤1;

2) $\int_{0}^{\tau} \pi^{2}(t, x) \mathrm{d} t<\infty \text { a. e. }$;

的控制策略(π(t，x)，q(t，x))为允许策略，又称允许策略的集合为可行集，记作Π.

对∀x≥0，用$J(x ; b)=E[D \mid \widetilde{R}(0)=x]$表示破产前阈值红利的累积现值的期望，则保险公司的目标是：使得最终阈值红利累积现值的期望达到最大，即

称其为最优分红函数. 为此，可构建如下的最优控制问题

满足

为了能得到最优控制问题的解，先给出以下检验性定理.

引理1^[20]  设W(x; b)为定义在[0，+∞)上的二次连续可微的函数，且W′(x; b)＞0，W″(x; b)＜0. 如果W(x; b)，V(x; b)分别是上述方程(4)与下述方程(6)和(7)的经典解，那么W(x; b)与V(x; b)一致，且满足HJB方程的(π^*(x)，q^*(x))就是最优投资策略，即V(x; b)=W(x; b)=J^π*，q*(x; b).

运用最优控制原理把本文的随机最优控制问题转化为Hamilton-Jacobi-Bellman(HJB)方程，再求解最优控制策略.

依文献[13]中2.5.1节的结论，阈值分红策略下的最优分红函数V(x; b)满足如下HJB方程. 当0≤x≤b时，

当x＞b时，

定理1  当x≥b时，便宜再保险下的最优投资-再保策略为

最优阈值分红函数为

其中

证  当x≥b时，对HJB方程(7)利用一阶最优性条件，可得

代入HJB方程(7)，有

其中，当0≤ρ＜1，η≥θ，μ₀＞r₀时，

很难得到方程(8)满足条件(5)的显式解. 而在η=θ的情形下，能得到方程的显式解，此时，再保险常被称为便宜再保险.

当B=0，不妨假设方程(9)有形如$V(x ; b)=\frac{\alpha}{\delta}+\frac{1}{k}\left(x-\frac{\alpha}{r_{0}}\right)^{k}\left(b-\frac{\alpha}{r_{0}}\right)^{1-k}$的解，则

且有

此时，方程(8)不难化为

显然

解得

不难证明0＜k＜1. 进而，可验证

满足边界条件(5)，故最优投资-再保策略为

定理2  当0≤x≤b时，便宜再保险下，最优投资-再保策略为

最优阈值分红函数为

其中

证  与定理1证明类似，这里不再赘述. 显然在δ=kr₀时，该解满足边界条件(5).

$\pi(t, x) \geqslant 0 \Leftrightarrow \frac{\mu_{0}-r_{0}}{\sigma_{0}} \geqslant \rho \frac{\sqrt{2 \lambda} \theta}{2}$，其经济学意义是：单位资本风险收益$\frac{\mu_{0}-r_{0}}{\sigma_{0}}$不低于保险单位风险收益$\frac{\sqrt{2 \lambda} \theta}{2}$带来的相关性风险收益$\rho \frac{\sqrt{2 \lambda} \theta}{2}$，这是因为投资风险资本的单位风险收益要比因承接的保险业务而给风险资本带来的相关性风险收益高的缘故.

$q(t, x) \geqslant 0 \Leftrightarrow \frac{\sqrt{2 \lambda} \theta}{2} \geqslant \frac{\mu_{0}-r_{0}}{\sigma_{0}}$，因此当且仅当$1 \times \frac{\sqrt{2 \lambda} \theta}{2} \geqslant \frac{\mu_{0}-r_{0}}{\sigma_{0}} \geqslant \rho \times \frac{\sqrt{2 \lambda} \theta}{2}$时，有π(t，x)≥0，q(t，x)≥0. $1 \times \frac{\sqrt{2 \lambda} \theta}{2} \geqslant \frac{\mu_{0}-r_{0}}{\sigma_{0}} \geqslant \rho \times \frac{\sqrt{2 \lambda} \theta}{2}$的经济解释是：单位资本风险收益$\frac{\mu_{0}-r_{0}}{\sigma_{0}}$不低于保险单位风险收益带来的相关性收益$\rho \frac{\sqrt{2 \lambda} \theta}{2}$，但却不超过保险单位风险收益$\frac{\sqrt{2 \lambda} \theta}{2}$，这是因为保险单位风险带来的收益一般来说要比资本单位风险带来的收益高的缘故; 这也是保险公司的主要业务是保险业务，而风险投资业务只是辅助业务的原因所在.

$q(t, x) \leqslant 1 \Leftrightarrow b \leqslant \frac{2 \lambda m \sigma_{0}}{\lambda \eta \sigma_{0}-\left(\mu_{0}-r_{0}\right) \sqrt{2 \lambda} \rho} \frac{\left(1-\rho^{2}\right)(1-k)}{1-\gamma}$，即只需阈值分红的分红界b在有界的范围内，就可保证q(t，x)≤1. 以下数值分析都在允许策略的等价条件下进行.

下面，首先将模型中涉及的保险参数x，m，λ，γ，投资参数r₀，μ₀，σ₀，α，保险风险与投资风险之间的相关系数ρ，结合文章中的结果，通过数值算例，对参数做数值分析，并作经济解释.

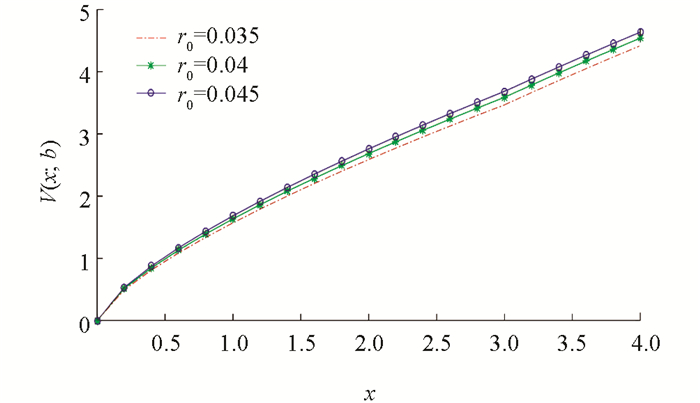
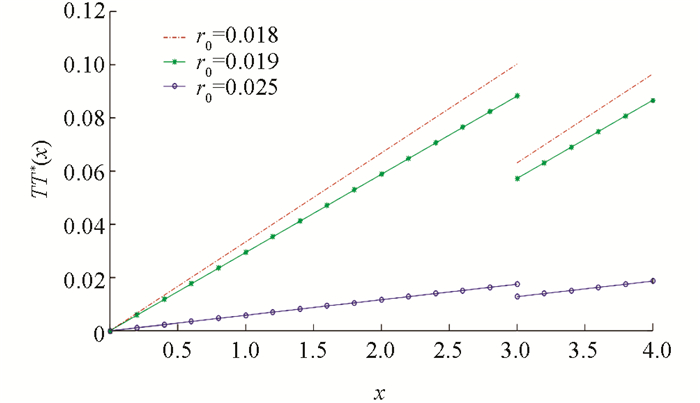
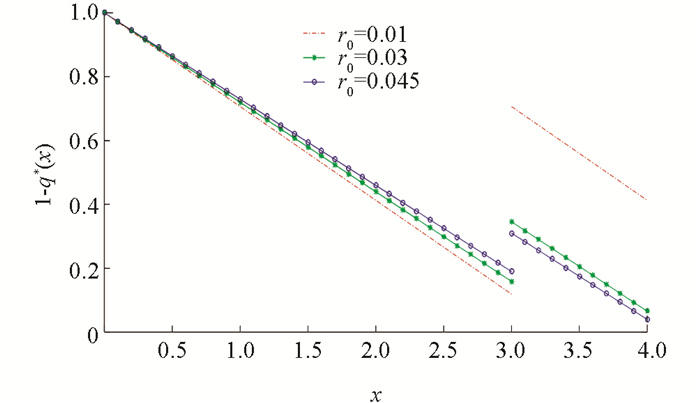
例1   先给出几个参数，λ=3，m=1，γ=0.3，η=θ=0.3，ρ=0.3，μ₀=0.1，σ₀=1，δ=0.2，α=0.02，b=3. 利用Matlab软件得到最优阈值分红函数与初始盈余和无风险利率之间的关系图(图 1)、最优投资策略与初始盈余和无风险利率之间的关系图(图 2)、最优再保策略与初始盈余和无风险收益率之间的关系图(图 3).

从图 1可以看出：最优阈值分红函数V(x)是初始盈余x的增函数，也是无风险利率r₀的增函数. 这是因为初始准备金越高，财富水平也越高，分红就越多; 无风险利率越大，无风险资本收益越多，财富水平越高，分红自然越多.

从图 2可以看出：初始盈余越大，即初始准备金越充足，此时为了追求更高的盈余水平，保险公司应该增加风险资本投资. 无风险利率越大，最优投资策略越小. 这是因为无风险资本投资能带来更多收益的情况下，保险公司当然会趋利避害，增加无风险资本的投资，降低风险资本的投资. 同时在分红界右侧，风险投资减少. 这是因为有分红的存在，财富减少，财富水平降低，减少风险资本投资有利于降低保险公司整体风险水平.

从图 3可以看出：最优再保策略是初始盈余的减函数，这是因为初始准备金越充足，整体风险水平越低，再保险的比例自然会下降. 在分红界的右侧，无风险资本利率增大. 由于风险资本投资减少，整体风险水平降低，保险公司的偿付能力提高，因此再保比例自然降低. 但在分红界左侧，为增强偿付能力，提高财富水平，应随无风险利率的提高继续增加再保险，以持续降低整体风险，尽快实现分红.

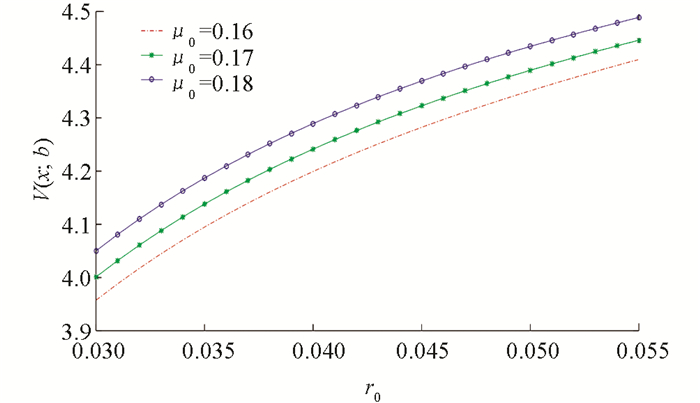
例2  先给出几个参数，λ=3，m=1，γ=0.3，η=θ=0.3，ρ=0.3，x=3.5，σ₀=0.5，δ=0.2，α=0.02，b=3. 利用Matlab软件得到最优阈值分红函数与无风险利率和资本风险收益率之间的关系图(图 4)、最优投资策略与无风险利率和风险资本收益率之间的关系图(图 5)、最优再保策略与无风险利率和风险收益率之间的关系图(图 6).

从图 4可以看出：最优阈值分红是无风险利率与风险利率的增函数. 这与资本收益率越高，投资回报越大，财富水平越高，分红越多的一般性认识一致.

从图 5可以看出：最优投资策略是无风险利率的减函数，是风险资本收益率的增函数. 这是因为无风险利率较高时，保险公司更愿意转投没有任何风险的无风险资产. 若风险资产收益率较高，则保险公司更愿意投资到风险资产，以取得更加可观的收益回报，来提高财富水平，增加分红.

从图 6可以看出：无风险利率越高，最优再保比例越小; 资本风险收益率越高，最优再保比例也越高. 这是因为无风险利率越高，转投无风险资产越多，回报会越多，财富水平提高，偿付能力提高，再保比例自然可以降低，此时更能增加分红，风险资本收益率增大. 由于风险投资增加，整体风险水平提高，此时自然需要提高再保比例，转移风险.

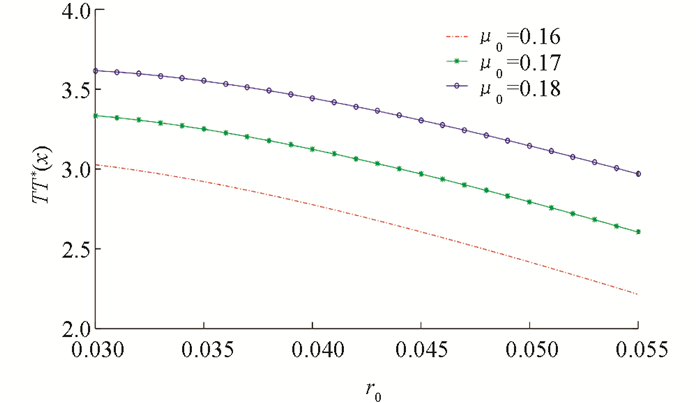
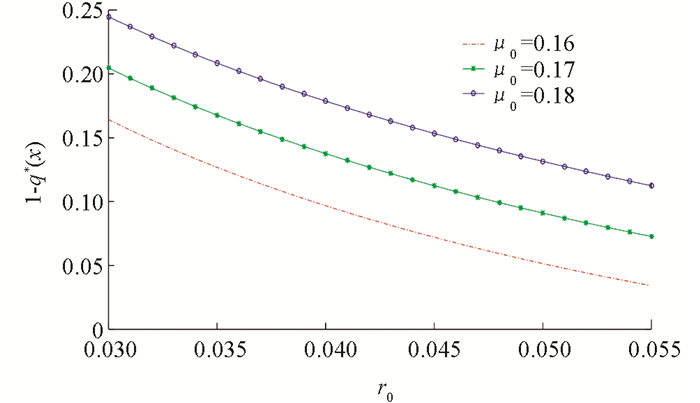
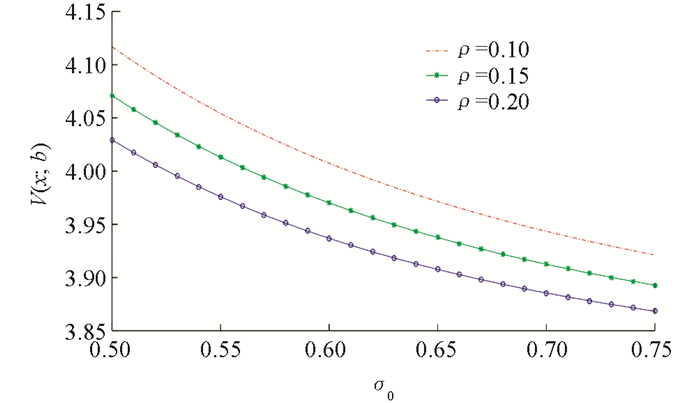
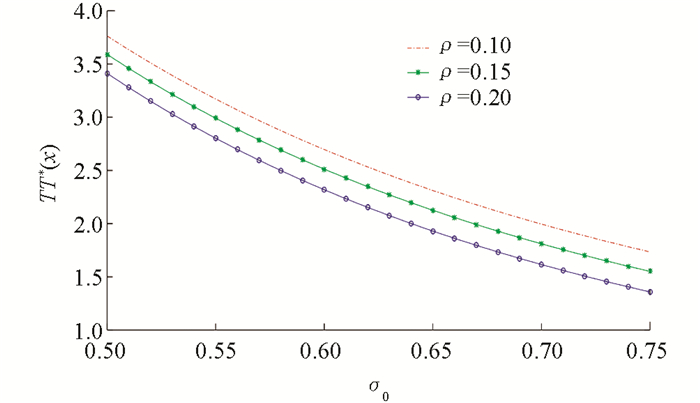
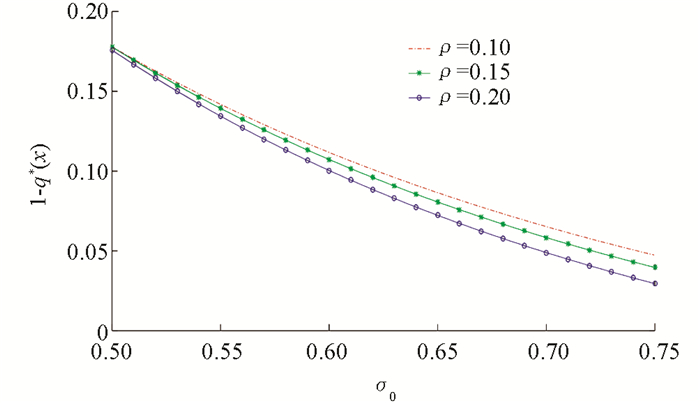
例3  先给出几个参数，λ=3，m=1，γ=0.3，η=θ=0.3，r₀=0.03，x=3.5，μ₀=0.16，δ=0.2，α=0.02，b=3. 利用Matlab软件得到最优阈值分红函数与资本风险波动率和相关系数之间的关系图(图 7)、最优投资策略与资本风险波动率和相关系数之间的关系图(图 8)、最优再保策略与资本风险波动率和相关系数之间的关系图(图 9).

从图 7可以看出：最优阈值分红函数V(x; b)是资本风险波动率σ₀和相关系数ρ的减函数，显然这与风险水平越高，分红越少的一般性认识一致.

从图 8可以看出：最优投资策略π^*(x)是资本风险波动率σ₀和相关系数ρ的减函数，这也与风险越大，风险投资应该减少的一般认识相一致.

从图 9可以看出：最优再保策略1-q^*(x)是风险资本波动率σ₀和相关系数ρ的减函数. 这是因为风险资本波动率越大，且相关性风险也越大时，整体风险增加，风险投资随之减少，整体投资风险降低，保险公司的赔付能力有所提高，所以降低再保比例反而更有利于分红.

文章考虑了无风险资本投资，完善了复合Poisson-Geometric风险下保险风险模型的研究. 从激发投保热情，增加投保人分红的角度看，投资收益率高的无风险资产显然更利于分红; 从风险控制的角度看，投资较高收益率的无风险资产显然能够降低风险资产投资所带来的风险; 从风险转移的角度看，投资高收益率的无风险资本时，则需要降低再保，此时反而更有利于分红.

在实际的金融市场中，无风险收益率并非始终是常数，而是跳跃的. 因此，考虑随机市场环境中的保险公司最优投资-再保-分红问题应该更能接近目前保险金融的实际运行状态. 探讨复合Poisson-Geometric风险下具有随机情形的分红问题将是一个值得研究的问题.