-
开放科学(资源服务)标志码(OSID):

-
青花椒Zanthoxylum schinifolium为芸香科植物,是十分重要的经济作物[1]. 青花椒是我国调味调料品的重要来源,且有药用价值,广泛种植于四川、重庆、云南、贵州等地[2]. 近年来,随着农业产业结构调整,其种植面积不断扩大[3]. 新鲜青花椒含水率高,在储存和运输过程中容易因霉烂、褐变而使品质降低. 对青花椒进行烘干处理可降低其含水率、延长储存时间、提升经济价值[4]. 传统堆积式烘干采用挖坑并结合砖砌构建烘房,坑部形成高度为400~500 mm的匀风室,上部堆积厚度为1.2~1.5 cm带枝花椒或净椒,烘房上部敞开或以麻袋覆盖,热源多为燃煤式热风炉,能耗高、污染重、安全性差,属于需淘汰的落后生产工艺装备. 采用空气能热泵作为替代热源,用工业绝热板材制成闭式烘房,自动控制水分排出,具有能效高、环境友好、安全性好、控制方便等优点,逐渐成为青花椒烘干领域的研究热点[5]. 烘房内流场均匀性决定了烘干速率、烘干品质和能耗. 国内外研究人员借助CFD(Computational Fluid Dynamics)对烘房内流场均匀性进行了相关研究,主要集中在改进烘房结构、增设辅助匀风装置两方面. 陈忠加等[6]、牛天宝等[7]探究了不同送风回风方式对烘房内部温度、速度均匀性的影响;师建芳等[8]、张健平[9]探究了烘房入口处不同风机数量对烘房内流场均匀性的影响;龚中良等[10]、代建武等[11]通过改变出风孔径、排列方式等来优化其内部流场;刘瑞等[12]针对气体射流冲击干燥机气流分配室提出了3种不同的优化结构;Wang等[13]通过在烘房进风口处安装引风罩优化烘房内流场分布;Song等[14]研究了入口气流速度、入口直径、隔板数量对西洋参干燥室内气流和温度分布的影响. 学者们还探究了烘房内不同形状、不同数量的导流板对其内部流场均匀性的影响[15-20];王鹏浩[21]探究了排风速度、导流板角度、导流板位置对空载和加载工况烘房内流场的影响;陈竹筠[22]探究了不同间距的格栅对热泵型海带烘房内气流的影响. 综上可知,烘房结构及导流板的设置都会影响其流场均匀性.
本文针对青花椒空气能热泵烘干装备,采用数值研究和实验研究相结合的手段,探讨导流板对青花椒堆积式烘干烘房内流场均匀性的影响,基于BBD试验和统计分析优化了导流板尺寸和工作参数,可为青花椒高品质绿色烘干工艺及烘房设计提供参考.
HTML
-
材料:青花椒(九叶青),2022年6月购于重庆市璧山区;细食用盐,用于密度法测量孔隙率.
仪器设备:5HGKB-4型空气能热泵烘干机(自制);WD412型风速传感器(杭州且远科技有限公司);FBS-760A型卤素水分测定仪(厦门市弗布斯检测设备有限公司);BSA224S-CW型电子天平(赛多利斯科学仪器(北京)有限公司);烧杯、量筒若干.
-
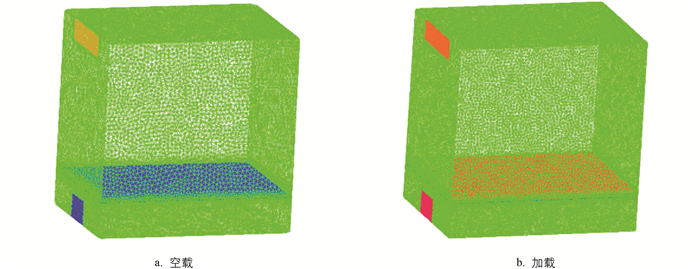
新鲜青花椒含水率为67.54%,鲜果直径5.5 mm. 参考文献[23]采用密度法测量孔隙率,如图 1所示. 青花椒堆积密度和真实密度分别为641.79 kg/m3和961.59 kg/m3,计算得到青花椒孔隙率为33.0%. 烘房加载方式如图 2所示,装载厚度为30 mm.
-
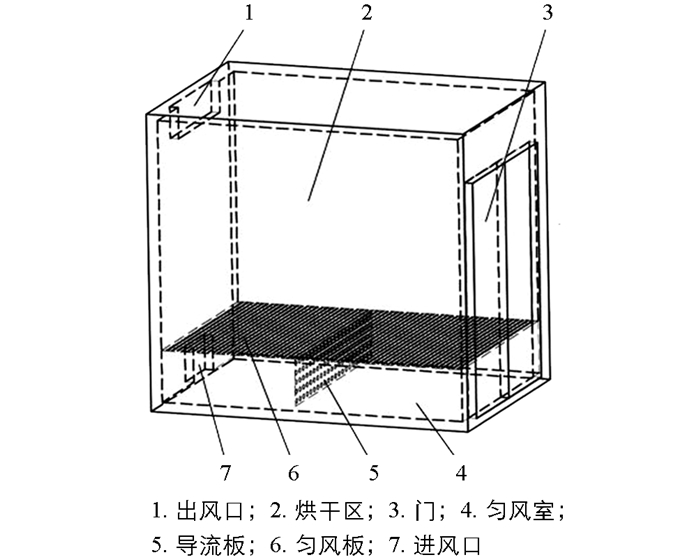
空气能热泵烘干机外形如图 3所示,其烘房由出风口、烘干区、门、匀风室、导流板、匀风板、进风口等组成,如图 4所示. 采用SolidWorks建立烘房三维模型,主要尺寸参数为:内腔长宽高1 800 mm×1 300 mm×1 800 mm;进风口330 mm×220 mm;出风口700 mm×200 mm;匀风板1 800 mm×1 300 mm;匀风板孔径3 mm、厚度3 mm、孔隙率18.1%;匀风室高度330 mm;门尺寸1 100 mm×1 500 mm(模型中当作壁面). 导流板尺寸根据实验方案确定.
建模时,为便于数值模拟和实验验证,进行如下处理:①不考虑烘房壁厚,绝热壁面;②不考虑匀风板厚度,并设置无厚度多孔跃升边界条件[24];③干燥介质空气视为不可压缩理想气体[25].
采用无厚度多孔跃升边界条件,可避免考虑匀风板上约6万个孔径为3 mm小孔带来的计算资源消耗问题. 30 mm装载厚度属于深床干燥范畴,可考察堆积式烘干在一定装载量条件下的烘房流场均匀性.
采用ICEM(International Council for Educational Media)软件对烘房三维模型进行非结构网格划分,如图 5所示. 为保证计算精度,进风口、出风口、匀风板及物料层的网格密度大于壁面. 空载烘房网格数量为2.67×106,加载烘房网格数量为2.8×106. 在进行网格无关性和模型可靠性验证时未考虑导流板;在进行单因素试验和BBD试验时,考虑导流板(图 6). 试验导流板参数包括导流板角度θ、导流板位置S、导流板长度L. 固定导流板其他参数,包括宽度300 mm、孔径15 mm、孔间距60 mm、厚度1 mm.
烘房边界条件及参数设置见表 1. 进风口选择速度入口,其大小由风速传感器测量得到;出风口选择压力出口;参考文献[27]计算入口、出口湍流强度及水力直径;匀风板选择多孔跃升[25];物料层设置为多孔介质,参考文献[24]方法测量孔隙率、黏性阻力系数及惯性阻力系数;烘房其他部分选择无滑移绝热壁面边界条件.
采用Ansys Fluent软件对三维模型求解,选择Realizable k-ε湍流模型及SIMPLE算法. 压强设置为标准大气压,在竖直方向重力加速度设置为-9.81 m/s2,采用混合初始化方式,收敛精度设置为1×10-4. Realizable k-ε模型中湍动能k和扩散率ε的方程分别为:
式(1)、式(2)中,ρ为密度,kg/m3;μ为层流黏性系数,Pa·s;μt为湍流黏性系数,Pa·s;xi,xj分别为位移在i,j方向上的分量,m;Gk为层流速度梯度产生的湍流动能,m2/s2;Gb为浮力产生的湍流动能,m2/s2;C1g,C2g,C3g为湍流经验常数;σk为湍动能的湍流普朗特常数;σε为耗散率的湍流普朗特常数. 模型参数设置同文献[22].
-
通过单因素试验分析导流板角度、导流板位置和导流板长度对烘房内流场及流场均匀性的影响,并确定BBD试验因子水平. 通过BBD试验确定各试验因子的影响程度,并优化导流板尺寸和工作参数. 表 2为单因素试验安排,试验号5,8,15具有相同的因子组合,仅试验1组. 表 3为BBD试验因子水平.
-
根据速度云图和速度不均匀系数评价烘房流场均匀性.
速度不均匀系数为监测平面上观测点速度均方差与平均速度的比值[26],可表达为:
式(3)、式(4)中,M为速度不均匀系数;σ为速度均方差,m/s;V为平均速度,m/s;N为观测点数量;Vi为观测点速度,m/s. 速度不均匀系数越小,表明该平面上的速度分布越均匀.
实测时,选取3个监测平面,其z坐标分别为600 mm、1 000 mm、1 400 mm,每个平面选取9个观测点,选取位置从平面中心向x和y方向双向展开,x方向间距为400 mm,y方向间距为250 mm,即x方向布置3行,y方向布置3列. x,y,z坐标设置见图 6. 测量时,每个观测点测量3组数据,每组数据100次重复. 仿真时,选取5个监测平面,其z分别为600 mm、800 mm、1 000 mm、1 200 mm、1 400 mm,每个平面选取377个观测点,选取位置从平面中心向x和y方向双向展开,x方向间距为60 mm,y方向间距为100 mm,即x方向布置29行,y方向布置13列.
1.1. 材料与仪器设备
1.2. 方法
1.2.1. 孔隙率测量和烘房加载
1.2.2. 仿真模型建立
1.2.3. 试验方法
1.2.4. 评价指标
-
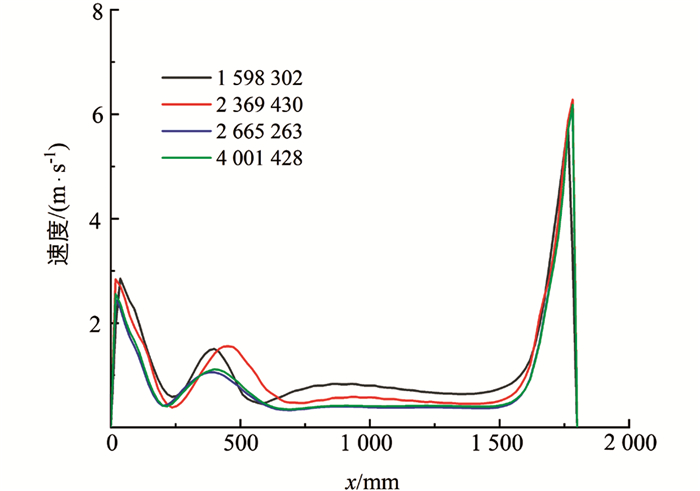
选择不同网格划分策略改变网格大小,得到1 598 302,2 369 430,2 665 263,4 001 428共4种网格数目进行网格无关性验证. 空载时在烘房坐标系中y和z分别为1 000 mm的两个平面交线上,验证不同网格划分策略下风速随x坐标位置的变化情况,如图 7所示. 由图 7可知,不同的网格划分策略风速随x坐标位置变化趋势基本相同,当网格数目为2 665 263时,增加网格数目对风速变化影响很小. 因此,为了减少计算量,采用网格数目为2 665 263的网格划分策略进行后续数值研究.
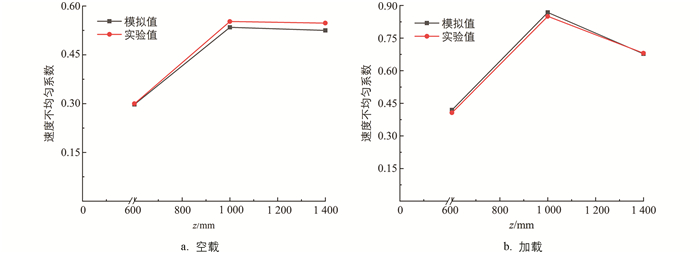
分别选取z坐标为600 mm、1 000 mm、1 400 mm 3个平面上的风速进行模型可靠性验证. 空载时3个平面各观测点风速模拟值和实验值数据见表 4. 3个平面风速模拟值和实验值相对误差的平均值分别为5.87%,5.78%,7.38%. 根据各观测点风速数据,可以计算出3个平面上基于模拟风速和实测风速的速度不均匀系数,如图 8a所示. 3个平面上模拟风速的速度不均匀系数分别为0.48,0.61,0.58,实测风速的速度不均匀系数分别为0.46,0.6,0.61,其相对误差分别为4.35%,1.67%,4.92%,平均为3.65%. 加载时,3个平面各观测点风速模拟值和实验值数据见表 5. 3个平面风速模拟值和实验值相对误差的平均值分别为9.87%,9.24%,9.16%. 3个平面上基于模拟风速和实测风速的速度不均匀系数,如图 8b所示. 3个平面上模拟风速的速度不均匀系数分别为0.42,0.87,0.67,实测风速的速度不均匀系数分别为0.41,0.85,0.68,其相对误差分别为2.44%,2.35%,1.47%,平均为2.09%. 风速和速度不均匀系数的试验和仿真结果表明,本文建立的仿真模型可靠性高,可用于后续相关研究.
-
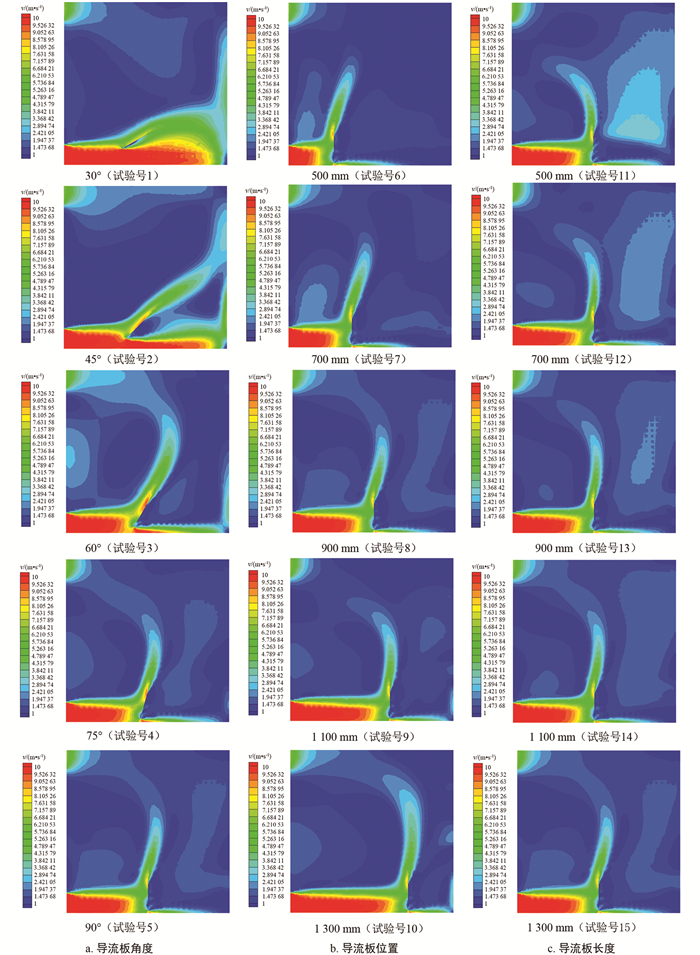
图 9和图 10分别为单因素试验风速的速度云图和速度不均匀系数影响图.
随着导流板角度增大,导流板对进风口高速流动气流的挡风效果增强,一部分气流流向烘干区,能够很大程度地避免匀风室内高速流体直接流向右侧(门侧),然后经上部空间直接回流出风口(图 9a). 与导流板角度30°,45°相比,导流板角度为60°,75°,90°时的速度不均匀系数更低(图 10a). 因此,选定导流板角度为60°,75°,90°进行后续BBD试验.
随着导流板位置的改变,导流板对进风口高速流动气流沿烘房空间分布作用明显,导流板太靠近进风口(如位置500 mm处)或太靠近右侧(如位置1 300 mm处)都不利于流场均匀性的提高. 导流板太靠近进风口,在右侧上方区域形成低速区;导流板太靠近右侧,在烘房中心区域形成低速区(图 9b). 与导流板位置500 mm、1 300 mm相比,导流板位置为700 mm、900 mm、1 100 mm时的速度不均匀系数更低(图 10b). 因此,选定导流板位置为700 mm、900 mm、1 100 mm进行后续BBD试验.
随着导流板长度的增加,导流板对进风口高速流动气流的挡风效果增强,使经导流板两侧流向烘房右侧的气流减少,速度云图均匀性降低(图 9c). 与导流板长度1 100 mm、1 300 mm相比,导流板长度为500 mm、700 mm、900 mm时的速度不均匀系数更低(图 10c). 但是,当监测平面高度增大到1 200 mm后,导流板长度为500 mm时的速度不均匀系数较大,且监测平面平均速度较低. 综合考虑,选定导流板长度为700 mm、900 mm、1 100 mm进行后续BBD试验.
-
使用Design-Expert 12中的Box-Behnken模块,以导流板角度、导流板位置和导流板长度作为试验因子,以z=1 000 mm平面上的速度不均匀系数为响应值,设计3因子3水平BBD试验. 表 6为BBD试验设计与结果,表 7为BBD试验方差分析.
由统计分析可知,A,AB,A2,B2和C2对速度不均匀系数影响极具有统计学意义,B,C对速度不均匀系数影响具有统计学意义(p<5%),其他项对速度不均匀系数影响不具有统计学意义. 各单因素对速度不均匀系数影响从大到小依次为导流板角度、导流板长度、导流板位置.
对表 7中数据进行回归拟合,剔除不具有统计学意义项,得到二次回归方程:
回归模型F=65.74>F0.05=6.94,p=0.0001<0.05,说明模型具有高的显著性;整体模型失拟项p=0.110 9>0.01,说明模型具有很高的可信度;回归方程的决定系数R2=0.991 6,调整系数RAdj2=0.976 5,说明回归方程的预测值和实验值拟合良好,即该模型能够较好地预测试验结果.
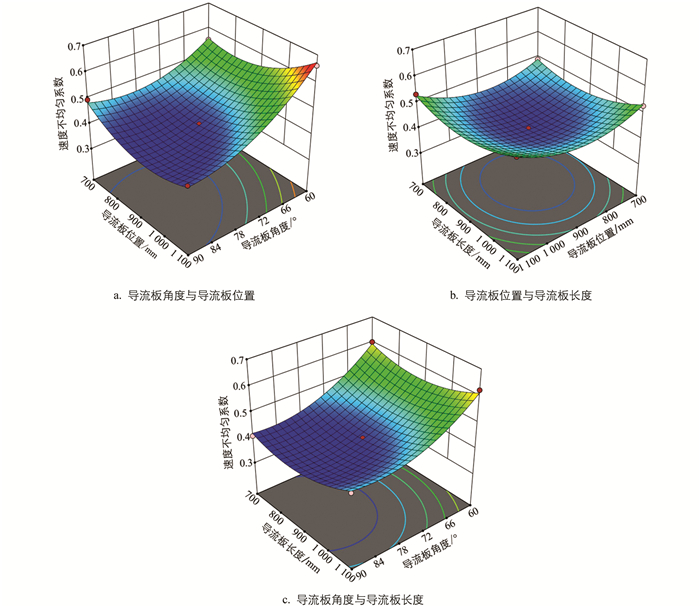
图 11为速度不均匀系数交互作用响应面图. 随着导流板角度及导流板与进风口距离增大,速度不均匀系数呈现出先减小后缓慢增加的趋势,导流板角度90°、导流板位置900~1 000 mm区间具有较低的速度不均匀系数(图 11a);随着导流板与进风口距离及导流板长度增大,速度不均匀系数呈现出先缓慢减小的后缓慢增加的趋势,导流板长度900 mm、导流板位置900 mm区域具有较低的速度不均匀系数(图 11b). 图 11c所示,较低速度不均匀系数对应导流板角度与导流板长度参数与图 11a和图 11b一致.
-
根据BBD试验回归方程,以速度不均匀系数最小为目标,得到最优导流板参数为导流板角度86.01°、导流板位置924.75 mm、导流板长度855.51 mm. 此时,z=1 000 mm平面上的速度不均匀系数预测值为0.384 9. 根据导流板最优参数,建立基于CFD的烘房三维模型并求解,可以得到不同平面上的速度不均匀系数模拟值. 其中,z=1 000 mm平面上的速度不均匀系数模拟值为0.3887. 预测值与模拟值之间的相对误差为0.98%. 分别选取z为600 mm、1 000 mm、1 400 mm 3个平面上的风速进行仿真与试验对比. 优化烘房空载时,3个平面各观测点风速模拟值和实验值数据见表 8. 3个平面风速模拟值和实验值相对误差的平均值分别为6.03%,6.43%,9.08%. 优化烘房加载时,3个平面各观测点风速模拟值和实验值数据见表 9. 3个平面风速模拟值和实验值相对误差的平均值分别为9.98%,8.70%,6.83%. 因此,该仿真结果与烘房内部实际结果相近,可用于探究烘房内部的流场变化.
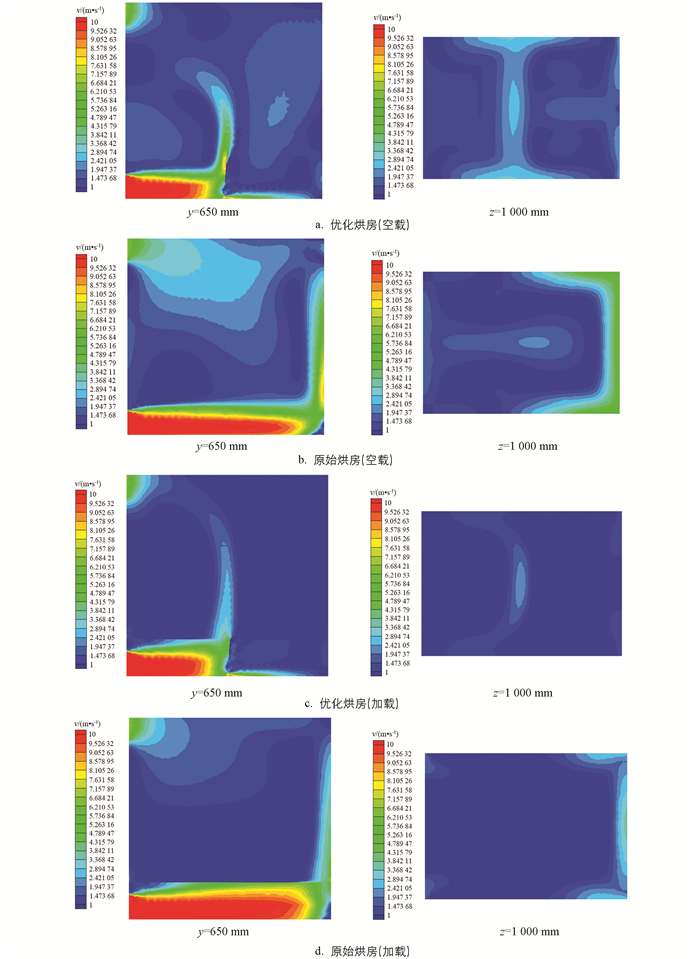
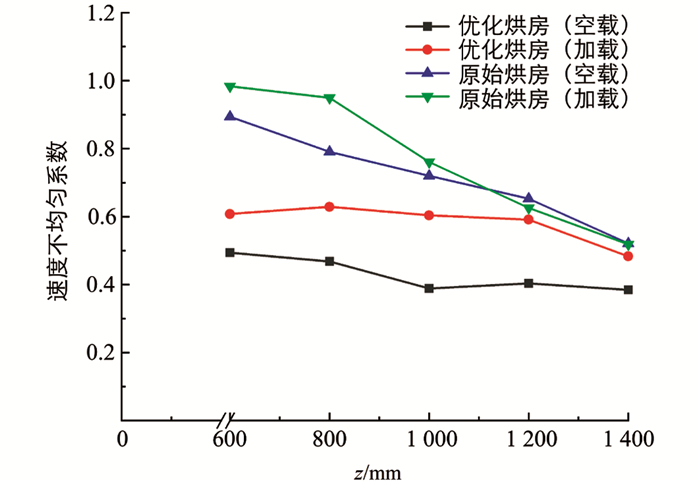
根据导流板最优参数,建立烘房三维模型,按照前述方法求解得到优化烘房流场速度云图,并与相同参数原始烘房(未安装导流板)进行比较,如图 12所示. 监测优化烘房和原始烘房截面高度600 mm、800 mm、1 000 mm、1 200 mm、1 400 mm各观测点风速,从而得到各水平面上的速度不均匀系数(表 10),并绘出速度不均匀系数随监测高度的变化曲线,如图 13所示.
由图 12可知,优化烘房流场受到导流板的作用,其上部烘干区域形成2个子区间,有利于烘干区域流场均匀性的提高,烘房加载后其流场均匀性有所降低. 由表 10和图 13可知,与原始烘房相比,优化烘房(空载)各截面高度平均速度不均匀系数降低39.2%,优化烘房(加载)各截面高度平均速度不均匀系数降低20.1%,烘房内流场均匀性得到较大提高.
2.1. 网格无关性及模型可靠性验证
2.2. 单因素试验
2.3. BBD试验
2.4. 烘房优化
-
1) 基于Realizable k-ε湍流模型和匀风板多孔跃升边界条件的烘房三维模型,对青花椒堆积式烘干流场及均匀性具有较高的可靠性. 空载和加载时监测截面上基于模拟风速和实测风速的速度不均匀系数平均相对误差分别为3.65%和2.09%.
2) 导流板参数对烘房内速度不均匀系数的影响从大到小依次为导流板角度、导流板长度、导流板位置. 以速度不均匀系数最小为目标,导流板最优参数为导流板角度86.01°、导流板位置924.75 mm、导流板长度855.51 mm.
3) 导流板使烘房上部烘干区域形成2个子区间,有利于烘干区域流场均匀性的提高. 与原始烘房相比,优化烘房(空载)速度不均匀系数降低39.2%,优化烘房(加载)速度不均匀系数降低20.1%,烘房内流场均匀性得到较大提高.











 DownLoad:
DownLoad: