-
深度神经网络[1-2]因为其良好的模式识别性能,在许多领域得到广泛应用[3-6].然而,当数据集较小或包含对抗性扰动样本时,其分类性能不够稳定,从而导致与纯净样本具有特征相似性的扰动数据的误分类.对抗性攻击能够泛化到不同的模型[7-8],因此如何准确评估不同分类器对于对抗性扰动的鲁棒性,并设计鲁棒性更强的分类器是机器学习的研究热点:文献[9]通过实验说明卷积网络对于某些变换不具备不变性;文献[10]提出对抗样本的快速生成方法—快速梯度符号法(FGSM,Fast Gradient Sign Method),虽然效率较高,但只给出最优扰动向量的粗略逼近,得到次最优解;文献[11]生成对抗性扰动,在训练过程中引入平滑度惩罚参数,提高分类器的对抗性扰动鲁棒性;文献[12]对不稳定现象进行理论研究,给出一些分类器的鲁棒性上界,但这些分类器比较简单;文献[13]提出神经网络的高复杂性可能是对抗性样本鲁棒性差的原因,通过L-BFGS(Limited-memory BFGS)算法[14]搜寻对抗样本,并利用对抗样本对模型进行规范化,提高鲁棒性,但是该方法耗时过长,难以应用于大型数据集.
为了解决上述问题,本文根据样本与分类器间的物理属性,定义样本的对抗性扰动,并利用线性迭代方法评估计算分类器的鲁棒性;通过标记对抗样本,对分类器进行优化,提高其分类性能.
HTML
-
对于一个已知分类器,本文将对抗性扰动ρ(x;
$\mathop y\limits^ \wedge$ )定义为能够改变分类标签$\mathop y\limits^ \wedge$ (x)的最小扰动向量r:其中:x为输入样本,
$\mathop y\limits^ \wedge$ (x)为分类标签,ρ(x;$\mathop y\limits^ \wedge$ )为分类器在x点的鲁棒性.则分类器的整体鲁棒性ρ($\mathop y\limits^ \wedge$ )定义如下:其中E为数据分布的期望.
-
本文首先提出用于二类分类器的算法.假定
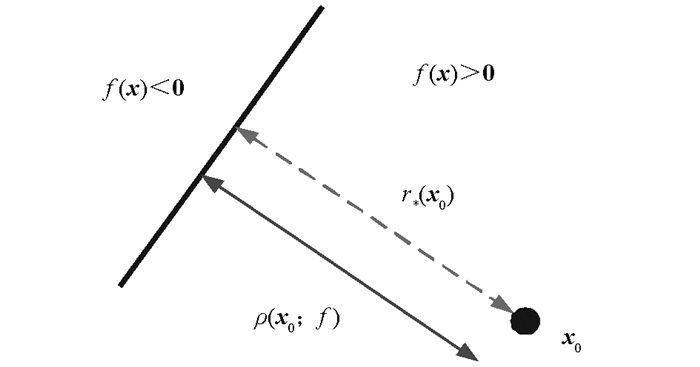
$\mathop y\limits^ \wedge$ (x)=sign(f(x)),f(x)为线性分类函数f(x)=wTx+b,Γ={x:f(x)=0}表示f的零水平集,即分类面.从图 1可以看出,f在点x0处的鲁棒性ρ(x0;f)与从x0到分类面Γ={x:wTx+b=0}的距离相等.影响分类器决策的最小扰动r*(x0)对应于x0在Γ上的正交投影,如式(3)所示.其中
$ {\rm{sign}}(f({\mathit{\boldsymbol{x}}_0})) = - \frac{{f({\mathit{\boldsymbol{x}}_0})}}{{\left\| \mathit{\boldsymbol{w}} \right\|_2^2}}\mathit{\boldsymbol{w}}$ .若f为非线性两类分类器,本文利用迭代过程计算其鲁棒性ρ(x0;f).每一次迭代时,在当前点xi周围对f进行线性化处理,该线性化分类器的最小扰动如式(4)所示.
第i步的扰动ri由式(3)求得,并对下一次迭代xi+1进行更新.当xi+1改变分类器的分类标签时,算法停止.具体过程如算法1所示.
实际中,该算法能够收敛至分类面Γ上的一个点.为了能够达到分类面的另一边,将最终扰动向量
${\mathit{\boldsymbol{\hat r}}} $ 乘以常数1+η,其中η≪1.本文取η=0.02.算法1
输入:样本x,分类器f
输出:扰动向量
${\mathit{\boldsymbol{\hat r}}} $ 初始化x0←x,i←0
while sign(f(xi))=sign(f(x0)) do
$ \mathit{\boldsymbol{r}}{_i} \leftarrow \frac{{f({\mathit{\boldsymbol{x}}_i})}}{{\left\| {\nabla f({\mathit{\boldsymbol{x}}_i})} \right\|_2^2}}\nabla f({\mathit{\boldsymbol{x}}_i})$ xi+1←xi+ri
i←i+1
end while
return
${\mathit{\boldsymbol{\hat r}}} = \sum\limits_i {{\mathit{\boldsymbol{r}}_i}} $
1.1. 对抗性扰动的定义
1.2. 鲁棒性计算
-
下面将抖动计算扩展到多类情况.假设分类器有c个输出,即类别数量为c,通过式(5)的映射关系进行分类.
其中fi(x)为分类器的第i个类别的输出.与二类分类器一样,首先对应于线性情况,然后扩展到非线性情况.
-
该种情况下,分类器函数f(x)=WTx+b最小扰动的计算如式(6)所示.
其中wi为矩阵W的第i列向量.几何学上,该问题为求解x0与凸多面体P的补集之间的距离,
其中x0位于P内,本文将该距离表示为D(x0,Pc).多面体P定义为分类函数f输出标签
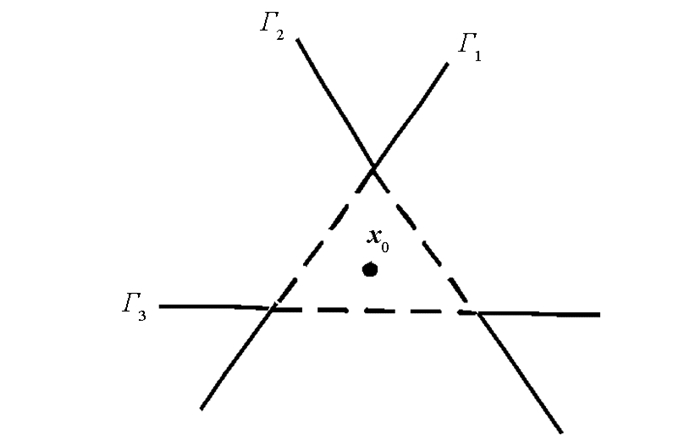
$\mathop y\limits^ \wedge$ (x0)的空间的区域,3条线围成的区域即为P(图 2).定义$\hat l$ (x0)为最接近P的界限的超平面,图 2中$\hat l$ (x0)=3.则$\hat l$ (x0)计算如式(8)所示:最小扰动r*(x0)为将x0投影到
$\hat l$ (x0)超平面上的向量,即x0到P表面的最短距离: -
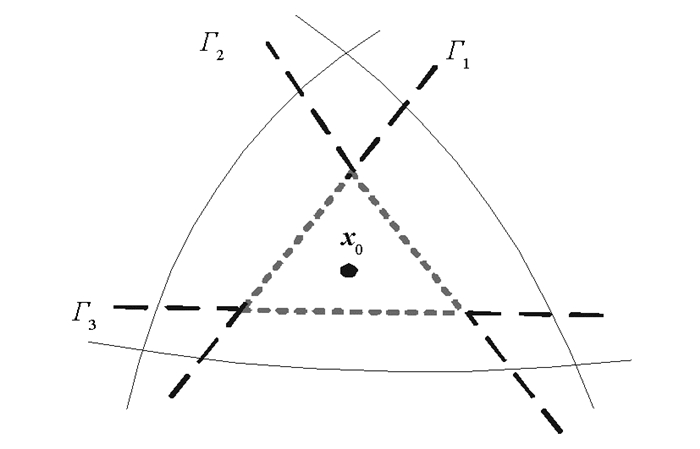
下面将扰动算法扩展到多类非线性分类器.对于多类非线性分类器,式(7)中输出标签
$\mathop y\limits^ \wedge$ (x0)所围区域集合P不再为规则多面体.同二类非线性分类器相似,本文通过一个规则多面体$ {{\tilde P}_i}$ 对第i次的集合P进行逼近,如图 3所示.各超平面包围的区域为P,虚线包围的区域为$ {\tilde P}$ ,计算公式如下:本文通过
$ D\left( {{\mathit{\boldsymbol{x}}_i}, \tilde P_i^c} \right)$ 逼近D(xi,Pc)的方法计算第i次迭代中xi与P补集之间的距离,即每次迭代计算xi到多面体$ {{\tilde P}_i}$ 边界的扰动向量,并对当前估计进行更新,具体如算法2所示.二类非线性分类器的算法1为具有自适应步长的梯度下降算法,每次迭代会自动选择步长.多类非线性分类器的算法2类似连续凸优化算法,每步迭代进行线性化约束.算法2
输入:样本x,分类器f
输出:扰动
${\mathit{\boldsymbol{\hat r}}} $ 初始化x0←x,i←0.
while
$\mathop y\limits^ \wedge$ (xi)=$\mathop y\limits^ \wedge$ (x0) dofor y≠
$\mathop y\limits^ \wedge$ (x0) dowy′←∇fy(xi)-∇f
$\mathop y\limits^ \wedge$ (x0)(xi)fy′←fy(xi)-f
$\mathop y\limits^ \wedge$ (x0)(xi)end for
$ \tilde l \leftarrow \mathop {\arg \min }\limits_{y \ne \mathop y\limits^ \wedge\left( {{\mathit{\boldsymbol{x}}_0}} \right)} \frac{{|f{'_y}|}}{{\left\| {\mathit{\boldsymbol{w}}{'_y}} \right\|_2^2}}$ $ {\mathit{\boldsymbol{r}}_i} \leftarrow \frac{{|f{'_{\hat l}}|}}{{\left\| {\mathit{\boldsymbol{w}}{'_{\hat l}}} \right\|_2^2}}\mathit{\boldsymbol{w}}{'_{\hat l}}$ xi+1←xi+ri
i←i+1
end while
return
${\mathit{\boldsymbol{\hat r}}}= \sum\limits_i {{\mathit{\boldsymbol{r}}_i}} $ -
上述算法基于l2范数对扰动进行度量,下面扩展到lp范数(p∈[1,+∞]).为实现该扩展,需要将算法2中的
$\hat l$ ,ri进行如下修改:其中:⊙为逐点乘积,
$ q = \frac{p}{{p - 1}}$ ,当p趋于无穷大时,q=1.
2.1. 线性分类器
2.2. 非线性分类器
2.3. 扩展lp范数
-
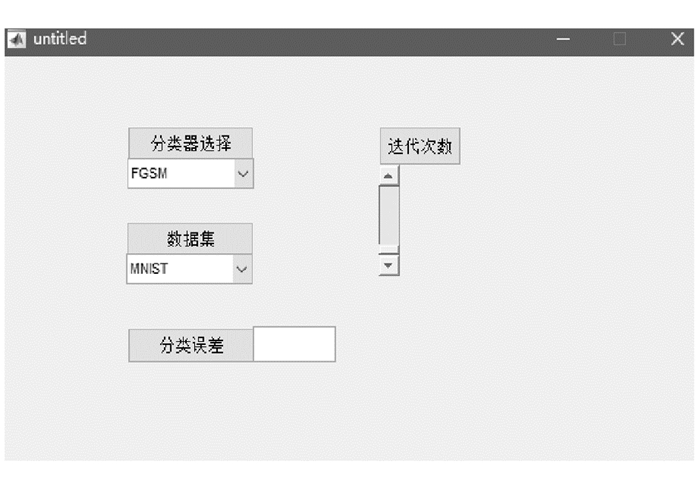
本部分实验以Matlab2016b为平台,软件仿真界面如图 4所示.处理器为英特尔Core i7 4800M 2.9 GHz;CUP内存为16 GB;操作系统为64位Windows 10.使用MNIST和CIFAR-10数据集分别训练Alexnet网络和ResNet网络分类器,对本文算法性能进行检验,同时与文献[10]的FGSM和文献[13]的L-BFGS两种算法进行比较.利用式(2)计算分类器对扰动的鲁棒性.
图像加入微小扰动后被误分类的示例如图 5所示.所用图像是CIFAR-10数据集中两幅图像.其中,第一行源图像是“鲸鱼”,加入一些扰动后,变成人眼很难区别的另一幅图像,但会被分类器错误分类为“海龟”.第二行源图像是“熊猫”,加入一些扰动后,分类器误分类为“长臂猿”.
-
不同方法对于MNIST和CIFAR-10数据集的结果,分别如表 1和表 2所示.
由表 1和表 2知,对于不同分类器,本文方法估计出的鲁棒性ρ最小,其更接近式(1)定义的最小对抗扰动.本文方法估计的鲁棒性与L-BFGS方法相近,但略小于后者;同时比FGSM方法小一个量级.说明本文方法在检测分类器网络扰动对抗方面具有更高的准确性.而FGSM方法和L-BFGS方法通过分类器的最小几何变换,给出分类器对几何变换鲁棒性的量化度量,且只能提供最优扰动向量的一个粗略逼近.同时由表 1和表 2知本文方法的运算时间远低于L-BFGS方法,略高于FGSM方法.因为L-BFGS方法涉及一系列目标函数最优化处理,时间复杂度较高.而本文方法经过较少的迭代次数就能够收敛到稳定的抖动向量结果,一般迭代次数为3即可.说明本文方法在提高扰动评估性能的同时,能够保持快速高效的计算效率,可有效应用于要求更深层复杂神经网络的大数据集情况.对于本文方法,每次迭代中影响分类器决策的最小扰动、对应于x0在Γ上的正交投影值如表 3所示,可以看出,在3次迭代后,其投影值基本处于稳定状态.
-
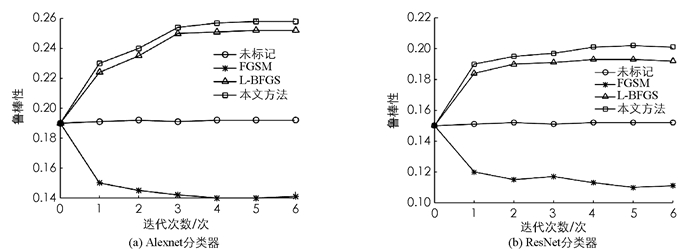
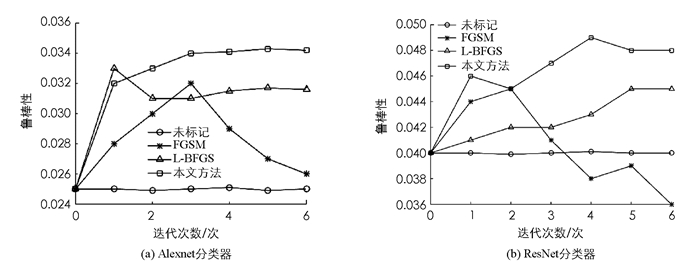
扰动性分析只是初步对分类器网络的性能进行评估,最终的目的是提高分类器网络的分类准确度.为了进一步分析本文方法的性能,本节实验分别利用FGSM方法、L-BFGS方法和本文方法标记对抗性样本,然后利用该对抗性样本对分类器性能进行微调优化,提高鲁棒性.本节实验在3.2节训练网络的基础上增加6次迭代,并且仅在扰动训练集上将学习率降低50%.分类器优化后,统一使用本文方法评估其鲁棒性.对MNIST数据集和CIFAR-10数据集采用未添加对抗样本、FGSM方法标记对抗样本、L-BFGS方法标记对抗样本、本文方法标记对抗样本4种方法进行微调,6次迭代的分类器鲁棒性分别如图 6和图 7所示.对于图 6的MNIST数据集,可以看出,本文方法比其他方法的曲线更早达到平稳的态势,即更快达到收敛状态.对于图 7的CIFAR-10数据集,除了本文方法,其他方法表现出没有规律的鲁棒性变化,而本文方法变化平稳.
由图 5和图 6可以看出,对分类器进行优化后,本文方法所获得的鲁棒性明显提高,优于其他方法,在增加3次迭代后,分类器性能趋于稳定. L-BFGS方法对分类器进行优化后,效果较本文稍差一些,但明显优于FGSM方法. FGSM方法的效果较差,这是因为FGSM输出含有严重受扰动的图像,并导向那些不会出现在测试数据中的图像.由此降低了该方法的性能. L-BFGS拥有一个不代表原始数据分布的正则项,稍微弱于本文方法.对于图 6的MNIST数据集,分类器优化后鲁棒性反而随着迭代次数的增加逐渐降低;对于图 7的CIFAR-10数据集,分类器优化后鲁棒性不稳定.出现该情况是由于FGSM方法估计出的扰动远大于本文方法的最小扰动,使用扰动性过大的样本对网络进行调整,降低了该网络对扰动的鲁棒性.
为了进一步说明本文方法的良好性能,对各方法优化后分类器的分类误差进行比较.分类误差的定义如下:
其中:sl表示理论基准分类率,t表示本次实验准确分类的样本数,S表示总样本数.
不同方法的优化结果如表 4所示.可以看出,FGSM方法由于标记出的抖动样本不准确,致使优化之后分类器的性能反而有所下降,分类误差上升. L-BFGS方法和本文方法通过正确标记抖动样本,优化后的分类误差明显更低,这主要得益于多类非线性分类器的性能,使得最优扰动向量的逼近值更佳.其中,本文优化后的每次迭代投影值如表 5所示,与表 3相比,投影值趋于稳定的速度更快,这也从另一个侧面说明优化后的鲁棒性更佳.
3.1. 鲁棒性评估
3.3. 分类器优化
-
本文提出一种新的扰动评估方法,其基于分类器的线性迭代评估能够改变分类标签的最小扰动,同时将该方法扩展到多类非线性分类器.对不同数据集和分类器进行的比较实验表明,本文方法在计算对抗性扰动方面更加准确高效.同时本文利用该方法生成扰动样本,对分类器进行优化调整,进一步提高分类器的性能.因此,本文提出的方法能够有效用于对最小扰动向量的准确估计,并构建鲁棒性更高的分类器.







 DownLoad:
DownLoad: