Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2019 Volume 44 Issue 11
Article Contents
Previous Article Next Article

Zhi-meng JIANG, Xiang HOU, Jie LI. Image Watermark Mixing Method Based on High Frequency Component Correction[J]. Journal of Southwest China Normal University(Natural Science Edition), 2019, 44(11): 102-109. doi: 10.13718/j.cnki.xsxb.2019.11.016
Citation: Zhi-meng JIANG, Xiang HOU, Jie LI. Image Watermark Mixing Method Based on High Frequency Component Correction[J]. Journal of Southwest China Normal University(Natural Science Edition), 2019, 44(11): 102-109. doi: 10.13718/j.cnki.xsxb.2019.11.016
shu

Image Watermark Mixing Method Based on High Frequency Component Correction

  • 1.

    Center of Information construction and service center, Sichuan University of arts and science, Dazhou Sichuan 635000, China

  • 2.

    School of intelligent Manufacturing, Sichuan University of arts and science, Dazhou Sichuan 635000, China

  • 3.

    Department of Science and Technology, Sichuan University of Arts and Science, Dazhou Sichuan 635000, China

More Information
  • Received Date: 27/06/2018
    Available Online: 20/11/2019

  • MSC: TP309

  • Aiming at the robustness of image watermarking under attack in image copyright protection, an image watermarking hybrid method based on high frequency component modification (HFCM) has been proposed in this paper. In the embedding part, the original image is preprocessed by Gaussian low-pass filter. Then, a secret key is used to randomly select a number of gray levels and the histogram of the filtered image with respect to these selected gray levels is constructed. After that, a histogram-shape-related index is introduced to choose the pixel groups with the highest number of pixels and a safe band is built between the chosen and non-chosen pixel groups. A watermark embedding scheme based on HFCM mechanism has been proposed, which embeds the watermark into the selected pixel group to further improve the robustness. At the decoding end, based on the available secret key, the watermarked pixel groups are identified and watermarks are extracted from them. Experimental results show that the proposed algorithm is robust to different attacks, and its performance is better than other algorithms.
  • 加载中
  • [1] MISHRA A, AGARWAL C, SHARMA A, et al.Optimized Gray-Scale Image Watermarking Using DWT–SVD and Firefly Algorithm[J].Expert Systems with Applications, 2014, 41(17):7858-7867. doi: 10.1016/j.eswa.2014.06.011

    CrossRef Google Scholar

    [2] GUPTA V, BARVE M A.Digital Watermarking Techniques: Review[J].International Journal of Advanced Research in Computer Science and Software Engineering, 2017, 7(1):7-9. doi: 10.23956/ijarcsse/V7I1/0153

    CrossRef Google Scholar

    [3] GUPTA M K, PANT D R.An Approach for Image Copyright Protection by Using Walsh Hadamard Method[J].Journal of the Institute of Engineering, 2017, 12(1):142-168. doi: 10.3126/jie.v12i1.16890

    CrossRef Google Scholar

    [4] BENYOUSSEF M, MABTOUL S, EL MARRAKI M, et al.Medical Image Watermarking for Copyright Protection Based on Visual Cryptography[C]//2014 International Conference on Multimedia Computing and Systems (ICMCS), New Yrok: IEEE, 2014.

    Google Scholar

    [5] MAKBOL N M, KHOO B E, RASSEM T H.Block-Based Discrete Wavelet Transform-Singular Value Decomposition Image Watermarking Scheme Using Human Visual System Characteristics[J].IET Image Processing, 2016, 10(1):34-52.

    Google Scholar

    [6] 陆璐, 杨志献, 姜永亮.一种基于HVS的DWT数字水印算法研究[J].西南师范大学学报(自然科学版), 2016, 41(11): 165-169.

    Google Scholar

    [7] ALI M, AHN C W, PANT M, et al.An Image Watermarking Scheme in Wavelet Domain with Optimized Compensation of Singular Value Decomposition Via Artificial Bee Colony[J].Information Sciences, 2015, 301:44-60. doi: 10.1016/j.ins.2014.12.042

    CrossRef Google Scholar

    [8] SOLTANI P A, VAN SCHYNDEL R, SELLIS T.Towards an Asynchronous Aggregation-Capable Watermark for End-to-end Protection of Big Data Streams[J].Future Generation Computer Systems, 2017, 72:288-304. doi: 10.1016/j.future.2016.09.001

    CrossRef Google Scholar

    [9] CEDILLO-HERNÁNDEZ M, GARCÍA-UGALDE F, NAKANO-MIYATAKE M, et al.Robust Hybrid Color Image Watermarking Method Based on DFT Domain and 2D Histogram Modification[J].Signal, Image and Video Processing, 2014, 8(1):49-63. doi: 10.1007/s11760-013-0459-9

    CrossRef Google Scholar

    [10] ZEAR A, SINGH A K, KUMAR P.A Proposed Secure Multiple Watermarking Technique Based on DWT, DCT and SVD for Application in Medicine[J].Multimedia Tools and Applications, 2018, 77(4):4863-4882. doi: 10.1007/s11042-016-3862-8

    CrossRef Google Scholar

    [11] DAS C, PANIGRAHI S, SHARMA V K, et al.A Novel Blind Robust Image Watermarking in DCT Domain Using Inter-Block Coefficient Correlation[J].AEU-International Journal of Electronics and Communications, 2014, 68(3):244-253. doi: 10.1016/j.aeue.2013.08.018

    CrossRef Google Scholar

    [12] ZONG T R, XIANG Y, NATGUNANATHAN I, et al.Robust Histogram Shape-Based Method for Image Watermarking[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2015, 25(5):717-729. doi: 10.1109/TCSVT.2014.2363743

    CrossRef Google Scholar

    [13] AGOYI M, ÇELEBI E, ANBARJAFARI G.A Watermarking Algorithm Based on Chirp z-Transform, Discrete Wavelet Transform, and Singular Value Decomposition[J].Signal, Image and Video Processing, 2015, 9(3):735-745. doi: 10.1007/s11760-014-0624-9

    CrossRef Google Scholar

    [14] WANG W, LI W H, LIU Y K, et al.A SVD Feature Based Watermarking Algorithm for Gray-level Image Watermark[J]. Journal of Computers, 2014, 9(6):1497-1502.

    Google Scholar

    [15] ZHANG Y P, WANG C Y, WANG X L, et al.Feature-Based Image Watermarking Algorithm Using SVD and APBT for Copyright Protection[J].Future Internet, 2017, 9(2):13. doi: 10.3390/fi9020013

    CrossRef Google Scholar

    [16] KISHORE R R.Digital Watermarking Based on Visual Cryptography and Histogram[J].World Academy of Science, Engineering and Technology, International Journal of Computer, Electrical, Automation, Control and Information Engineering, 2016, 10(7):1264-1269.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(7)  /  Tables(3)

Export Citation
PDF
XML

Article Metrics

Article views(782) PDF downloads(105) Cited by(0)

Access History

Other Articles By Authors

Image Watermark Mixing Method Based on High Frequency Component Correction

  • Received Date: 27/06/2018
  • Available Online: 20/11/2019

Abstract: Aiming at the robustness of image watermarking under attack in image copyright protection, an image watermarking hybrid method based on high frequency component modification (HFCM) has been proposed in this paper. In the embedding part, the original image is preprocessed by Gaussian low-pass filter. Then, a secret key is used to randomly select a number of gray levels and the histogram of the filtered image with respect to these selected gray levels is constructed. After that, a histogram-shape-related index is introduced to choose the pixel groups with the highest number of pixels and a safe band is built between the chosen and non-chosen pixel groups. A watermark embedding scheme based on HFCM mechanism has been proposed, which embeds the watermark into the selected pixel group to further improve the robustness. At the decoding end, based on the available secret key, the watermarked pixel groups are identified and watermarks are extracted from them. Experimental results show that the proposed algorithm is robust to different attacks, and its performance is better than other algorithms.

    HTML

  • 随着互联网技术的迅速发展，数字图像的获取变得更加容易.然而，随着数字图像的轻松获取，数字图像的非法复制数量不断增加，并没有考虑该图像上的现有版权问题[1-2].此外，许多数字图像处理软件更容易对数字图像进行快速操作和修改，从而增加了盗版和滥用数字图像版权的机会[3-4].图像水印是识别所有者问题的一个解决方案[5-6]，数字水印可以是插入数字文件(如图像，音频或视频)的比特模式.数字水印的一个重要特征是对多种类型的攻击或常见图像操作(如旋转、过滤、缩放、裁剪和压缩)的鲁棒性和不可感知性.数字水印算法的效能完全基于嵌入水印对多种攻击的鲁棒性.现有的水印方法能够有效解决信号处理攻击，但是不能很好地应对几何攻击，为了解决几何攻击，已经在图像水印中使用了各种技术，这些技术可以大致分为非盲水印技术和盲水印技术[7].非盲水印技术需要在解码端使用主图像进行水印提取，因此在实际使用中局限性较大，而盲水印技术不需要解码器中的主图像信息，使得其更适合于现实世界的应用.

    大多数盲水印技术可分为穷举搜索、变换域、模板和基于特征的技术，但是穷举搜索方法在计算上非常昂贵，且错误检测率很高[8].对于文献[9]中水印嵌入在DFT变换域中实现，该域对于缩放和旋转是不变的，但是容易受到裁剪的影响.文献[10]中HWT-DCT图像水印算法易受到随机弯曲攻击的影响.文献[11]中DCT图像水印算法在信号处理攻击和一些几何攻击(例如缩放和旋转)方面表现不佳.文献[12]中将线结构应用于模板，在文献[13]中chirp-Z变换用于更准确和更快速的模板匹配，基于模板的方法主要缺点是攻击者可以估计模板，然后将其删除，由于图像信息永久丢失，这种方法不能保证在剪切攻击下成功提取嵌入的水印.在文献[14]和[15]中，图像的空间统计特征被用于提取矩不变量，然后用于水印嵌入，这种方法对于仿射攻击是不变的，但它极易受到裁剪攻击的影响.

    为了解决现有方法的问题，本文提出一种基于直方图-哈夫曼编码的HFCM混合图像水印算法，该算法在嵌入阶段首先构造高斯滤波图像的直方图与使用密钥随机选择的多个灰度级，直方图形状相关索引来选择像素数最多的像素组，并在选定和未选像素组之间建立一个安全带，通过将一些像素移动到像素组内的某些灰度级，将水印位插入到所选组中，并在水印嵌入过程中，提出一种新的高频分量修正(HFCM)方案来补偿高斯滤波的副作用，从而进一步增强了鲁棒性.

1.   高斯滤波和Huaffman编码

    1.1.   高斯滤波

  • 通过将水印嵌入到图像的低频分量中，可以实现对常见信号处理攻击的鲁棒性.因此，首先通过二维高斯低通滤波器对灰度图像I进行预处理.

    其中，(x，y)表示像素的位置，σ是高斯分布的标准差，一般选择σ=1.滤波后的图像Ilow可以表示为

    其中，*表示卷积运算.如果Ihigh代表从主图像I去除高斯滤波的高频分量，则表示为

    实际上，通常使用表达式(2kσ+1)2来选择高斯掩模F的大小，其中k是正整数.由于高斯分布99.7%的能量集中在平均值的3个标准偏差内，可以将k设置为3.因此，本文使用的高斯掩模F的大小为7×7.

    • 1.2.   Huffman编码

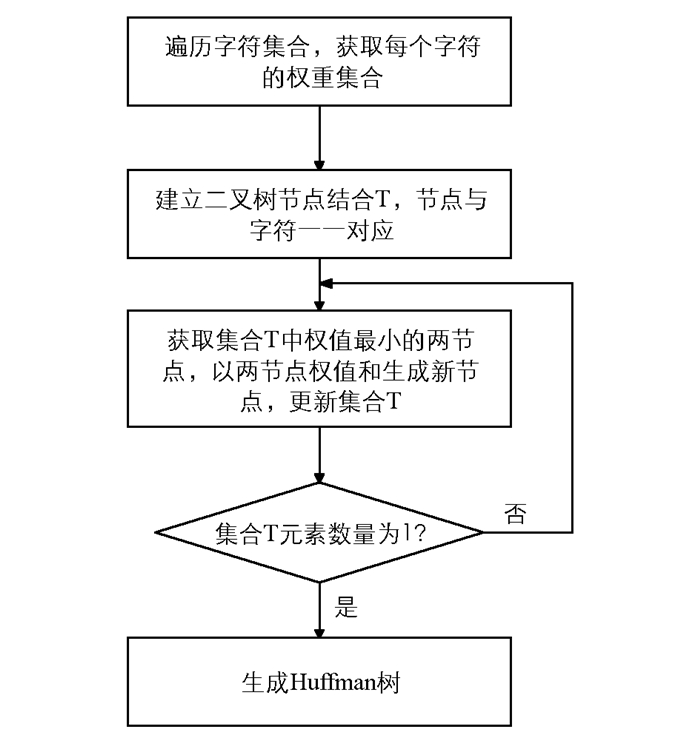
  • Huffman编码可用于压缩信息，原始宿主图像被转换为比特序列，并且根据每个符号的出现频率制作霍夫曼字典.根据字符串内出现的次数选择概率，然后使用该字典对图像的高频分量进行霍夫曼编码.该编码序列再次进行算术编码，以获得更好的结果. Huffman编码是基于Huffman树结构的，构建Huffman树的流程见图 1.

    遍历树种子节点和根节点路径，设定左节点编码为0，右节点编码为1，对各个节点进行编码.

2.   基于HFCM的水印混合方法

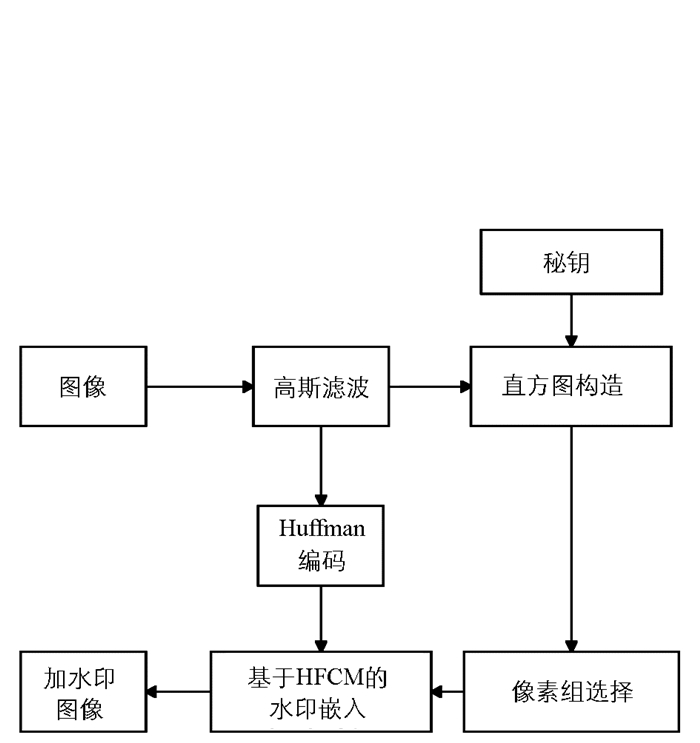
  • 本文所提方法的水印嵌入过程如图 2所示，该算法由4个步骤组成：高斯滤波、直方图构造、像素组选择和基于HFCM的水印嵌入.

    • 2.1.   直方图构造

  • 假设滤波图像Ilow低具有K灰度级，8位灰度图像具有K=256灰度级，范围从0到255，直方图的形状与图像内容相关，用于提取隐藏在图像中的数据.使用长度为K的伪噪声(pseudo-noise，PN)序列作为安全密钥，从K个可用灰度级中随机选择S个灰度级，其中$\frac{K}{2}$≤S < K. p(n)每个元素随机取[0，K－1]范围内的整数，K1，…，KS表示S选择的灰度级，则图像Ilow的直方图可以表示为

    其中，hS(Ki)是对应于灰度级Ki的像素数量.

    • 2.2.   像素组构造

  • 在构造直方图HS之后，取HS中的LB个相邻灰度级来形成一个bin，则第i个bin中像素数为

    其中：LB为一常数，表示相邻灰度级的个数，i=1，2，…，MB，MB=$\left\lfloor {\frac{S}{{{L_B}}}} \right\rfloor , \left\lfloor \cdot \right\rfloor $取整函数，两个相邻的bin组合起来形成一个组，总共有$\frac{{{M_B}}}{2}$组，对于第i组，两个bins(Bin_1和Bin_2)分别包含hB(2i－1)和hB(2i)个像素.其中i=1，2，…，$\frac{{{M_B}}}{2}$，则第i组中的像素数为

    设Ns是对应于S选择灰度级的像素总数.

    为了使像素组的选择适应直方图形状，基于hG(i)和NS之间比率的像素组选择标准为

    如果g(i)大于预定阈值TG，则选择i个像素组用于水印嵌入，该阈值TG用于平衡鲁棒性和嵌入率，TG值越大，由于组中像素越多，鲁棒性越高，但是水印嵌入的像素组越少，嵌入率就越低.本文将TG作为经验选择TG=图像总像素数/4LB.设LG为适合嵌入水印的像素组，其中LG≤$\frac{{{M_B}}}{2}$.

    在水印解码过程中，g(i)值将被估计，然后用于识别包含水印的LW像素组，g(i)的值在攻击后会有所变化，导致识别加水印像素组时会出错.为了消除这种情况，针对LW选择像素组和嵌入过程中未选择像素组之间的g(i)引入安全带.

    假设gmin是LW选择像素组中的最小g(i)值，安全带的宽度设置为α·gmin，其中α是控制安全带强度的参数.对于每个非选择组中随机选取的[g(i)-(1-α)·gmin]·NS像素，如果相应的g(i)满足(1-α)·gmin < g(i) < gmin，则这些像素的灰度值被改变，使得其落入最接近的选定组中，形成宽度为α·gmin的安全带.

    • 2.3.   基于HFCM的水印嵌入

  • 水印的嵌入式通过bins之间像素传输实现，设w1，w2，…wLW分别是嵌入到LW选择组中的水印比特，每选择第i个组由两个bins组成：(Bin_1和Bin_2)，分别包含hB(2i－1)和hB(2i)个像素，可以使用式(9)中嵌入规则将水印wi嵌入到第i个选择组中.

    如果wi=1，一定数量的像素(比如N1)应该从Bin_2转移到Bin_1，使得hB(2i－1)≥2hB(2i)；如果wi=0，应当将N0像素从Bin_1转移到Bin_2，使得hB(2i－1)≤$\frac{1}{2}$hB(2i). N0和N1的最小值定义为

    像素转移将影响图像的感知质量，为了获得更好的感知质量，像素值的变化应该很小.因此，使用新的像素传输方法来减小像素移动的程度，转移情况分两种：

    1) ${N_{{K_{i \cdot {L_B} + 1}}}}$≥N0，则将Bin_2中的N0像素从灰度级${K_{i \cdot {L_B} + 1}}$移动到灰度级${K_{i \cdot {L_B} + 2}}$，然后从Bin_1中选择N0个像素，Bin_1中选择的像素移动到Bin_2中的灰度级${K_{i \cdot {L_B} + 1}}$.

    2) ${N_{{K_{i \cdot {L_B} + 1}}}}$≤N0，从${K_{i \cdot {L_B} + 1}}$级灰度移动所有${N_{{K_{i \cdot {L_B} + 1}}}}$像素到${K_{i \cdot {L_B} + 2}}$级灰度，然后以1)中描述的方法从Bin_1的LB灰度级中选择N0像素.在这些选择的像素中，将第一个${N_{{K_{i \cdot {L_B} + 1}}}}$像素移动到灰度级${K_{i \cdot {L_B} + 1}}$，剩下的N0 -${N_{{K_{i \cdot {L_B} + 1}}}}$像素到灰度级${K_{i \cdot {L_B} + 2}}$.

    在不使用HFCM的情况下，用IlowW表示水印的低频分量，可以得到相应的水印图像IW=IlowW+Ihigh，其中Ihigh为图像的高频分量，设I′为水印解码阶段的接收图像.在没有攻击的情况下I′=IW，水印隐藏在图像的低频分量中，因此在编码和解码阶段使用相同的高斯掩模F，I′low是从水印图像提取的.

    如果I′low=IlowW，可以正确地提取水印嵌入在图像中.由于高斯滤波的副作用，两者不相等.

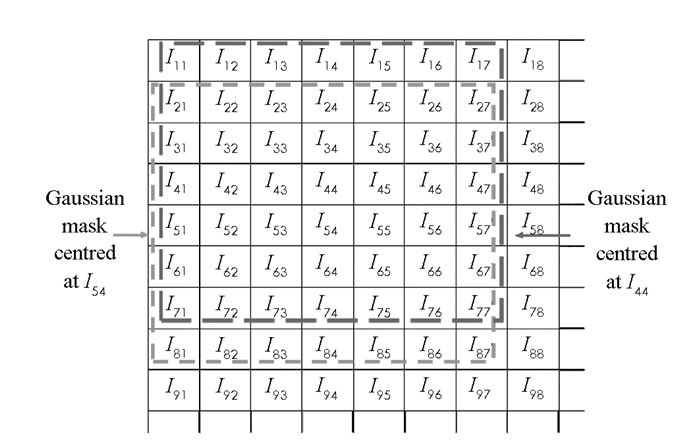
    为了正确地提取嵌入水印，需要对Ihigh进行适当修改，以补偿高斯滤波的副作用，使得嵌入端的水印低频分量等于其在解码端的对应分量.在Ilow的像素由于水印嵌入而改变之后，将通过HFCM修改Ihigh中的对应像素.如图 3所示，将高斯掩模F应用于以像素I44为中心的主图像I，I44的低频分量I44_low可以表示为

    由于水印嵌入，像素被ξ修改，得到水印的低频分量I44_lowW=I44_low+ξ.图像高频分量的修正量为${I_{44 - {\rm{high}}}} = \frac{{\left( {1 - {F_{44}}} \right)\xi }}{{{F_{44}}}}$，改变I44_high将影响相邻像素并降低感知质量.因此，引入参数β来控制HFCM的强度，I44_high=β*I44_high，其中β是一个常数.

    • 2.4.   水印解码过程

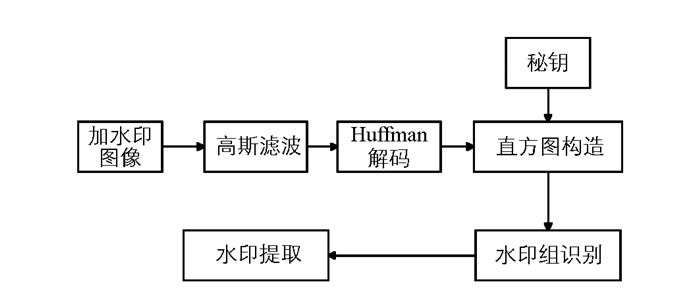
  • 水印解码过程包括高斯滤波、霍夫曼解码、直方图构造、水印组识别和水印提取，具体流程见图 4.

3.   实验结果与分析

  • 本文通过实验来评估所提方法的感知质量和鲁棒性，并和文献[10]和[16]中的方法进行比较.使用512*512大小的标准灰度图像作为主机图像评估本文水印算法，并且版权使用尺寸为32*32的二进制图像，选择6个标准灰度图像Lena，F16，Pepper，Shingboat，Entagon，Barbara用作实验图像.本文采用峰值信噪比(PSNR)、均方误差(MSE)、结构相似性(SSIM)指数和相关系数作为评估性能指标.

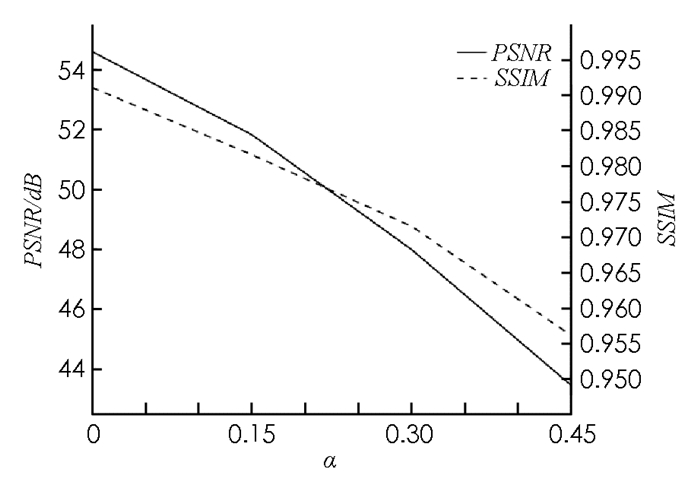
    本文算法参数经过多次实验，并根据经验选择S=246，LB=3，LW=25.对于α的选择，α控制安全带强度，从而控制鲁棒性. α越大，鲁棒性越好，增加α会导致更多的像素修改，从而对感知质量产生更多负面影响. 图 5(a)显示了当β=0时，α如何影响感知质量.

    可以看到，当α大于0.15时，进一步增加α只会对鲁棒性产生较小的改善，但会导致相当大的感知质量下降.因此，为了在保持良好感知质量的同时实现高鲁棒性，凭经验选择α= 0.15. β的选择：图 6给出β对感知质量和鲁棒性的影响，其中α= 0.15.

    由图 6可以看出，β的上升使得PSNR和SSIM均下降，这是因为较大的β意味着更强的HFCM，相当于像素高频分量的更多变化，导致感知质量降低.随着β值增加，PSNR和SSIM值减小，为了保持较高的感知质量，选择β= 0.1. 表 1给出了本文算法对不同图片的PSNR和MSE性能指标，表 2给出了本文算法与其他方法的性能比较.

    从表 1和表 2中数据可以看出，本文图像水印算法PSNR可达到50 dB以上，而其他两种算法在38~44.7 dB之间，远低于所提方法，说明本文算法感知性和鲁棒性较好，且性能优于其他两种算法. 图 7给出了不同类型的攻击，表 3给出了在图 7攻击影响下所提方法的提取水印关联系数，当没有攻击时，关联系数为1.

    从表 3数据可以看出，几种攻击的平均关联系数为0.919，说明本文方法具有良好的稳健性，这种良好的性能取决于3个因素：①由于使用了基于直方图形状的像素组选择标准，因此本文方法用于嵌入水印的像素组包含像素数多于其他方法中的像素数；②在本文方法中，用于水印嵌入的像素组和非选择像素组之间建立安全带；③本文方法使用独特的HFCM方案.

4.   结论

  • 本文提出一种新的图像水印方法，对常见攻击具有鲁棒性.为了处理信号攻击，采用高斯低通滤波器对宿主图像进行预处理，使得水印只嵌入到宿主图像的低频分量中.为了解决几何攻击，利用直方图形状相关索引来形成和选择最合适用于水印嵌入的像素组.此外，在所选择的像素组和未选择的像素组之间引入安全带，提高对几何攻击的鲁棒性.此外，提出了一种新的HFCM方案来补偿高斯滤波的副作用，从而进一步增强了鲁棒性.由于秘钥的使用，所提出的水印方法安全.实验结果验证了本文方法的可行性和有效性.

Figure (7)  Table (3) Reference (16)

Catalog

    Copyright Journal of Southwest China Normal University(Natural Science Edition)

    Address： Tel：023-68252540，68254576，68254478 E-mail：xbbjb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return