-
压缩感知(Compressed Sensing,CS)是一种信号处理框架,自21世纪初引入以来,在信号处理领域和应用数学领域引起了大量研究人员的关注,其核心思想就是采用通过线性测量的少量测量信号有效地重建原始信号[1-2]. CS的结果对众多信号处理应用产生重要影响,包括对音频[3],图像[4-5]和视频[6-7]等高维数据的高效处理和分析.
在压缩感知理论中,测量矩阵是一个重要组成部分,最经典的测量矩阵为高斯矩阵、伯努利矩阵,前者都是随机测量矩阵,虽然利用随机测量矩阵引入压缩感知,但是新的结果涉及比随机测量更有效的矩阵,从而产生较少的必要测量或更好的重建性能[8].随着CS理论越来越成熟,对于测量矩阵的研究也越来越多.文献[9]提出一种对随机测量矩阵的优化技术,该方法通过构建不连贯的单位规范紧密框架(Unit Norm Tight Frames,UNTF),使得随机测量矩阵的最大列相关性接近最小可能边界,从而提高重构性能.文献[10]将信号的先验知识纳入信号采集阶段,减少编码测量的次数,同时在解码器处完美实现信号重构.
对于随机矩阵的研究已经成熟,而确定性矩阵还有待研究,文献[11]给出一种确定性测量矩阵,使用嵌入操作将二进制矩阵与相关性较低的矩阵合并,这种嵌入操作具有更好的恢复性能.文献[12]在低密度奇偶校验(Low-density Parity-check,LDPC)矩阵基础上,提出一种类似托普利兹矩阵的压缩感知测量矩,该矩阵易于实现,具有更好的稀疏性.文献[13]分块的有序范德蒙矩阵具有线性不相关性质,实现了时域中的非均匀采样,使得块的有序范德蒙矩阵CS特别适合处理自然图像信号.
目前,CS的重要研究方向着重于CS的硬件实现,为了实现高效存储,快速编码和解码,已经提出了结构化矩阵,不过这些矩阵重构性能并不理想.针对以上问题,本文提出一种深度学习的稀疏测量矩阵压缩感知方法,采用深度学习方法来学习优化测量矩阵和从测量到原始信号的非线性重建过程.为了便于测量过程的硬件实现,使用{0,1,-1}组成稀疏三元矩阵,在所提出的网络架构上施加稀疏性和二元约束.实验结果表明,本文方法在包含5%的非零元素测量矩阵条件下,能够实现图像的高质量重建.
HTML
-
传统CS理论定义为:用满足条件的测量矩阵进行线性测量,对有限长度的实值信号x∈RN使用CS感测或投影矩阵实现感测机制产生经处理信号的压缩表示.线性测量过程可描述为
其中,y∈RM表示获得的测量值矢量,Φ∈RM×N为测量矩阵,测量矩阵满足有限等距性质(Restricted Isometry Property,RIP)条件,而对于信号x∈RN可用稀疏基和稀疏向量s表示,s中含有K个非零值,且K < < N.测量矩阵的RIP条件见式(2).
其中,0 < δk < 1.为了从其相应的测量向量y中获重构稀疏信号,需要寻找与测量向量y一致的最稀疏信号
$\mathop x\limits^ \wedge $ .满足式(1)中的稀疏向量,可以作为l1范数最小化问题的解,求得的解$\mathop s\limits^ \wedge $ 即能够得到重建信号,l1范数求解$\mathop s\limits^ \wedge $ 可表示为其中,‖·‖1表示矢量的l1范数,求解式(3)是一个NP-hard问题.因此,用l0范数来代替l1范数求解方程,可将式(3)转化为一个易处理和稳定的线性规划问题.这个线性规划可以基于凸优化方法或迭代贪婪算法来求解,这些算法一般是一阶方法,因此更适合于高维问题.
传统的CS理论基于随机高斯或随机Bernoulli矩阵,可用于恢复n维的稀疏信号s,条件是测量次数m为O(s log(n/s)),考虑随机矩阵时,一个重要的问题是这些矩阵通常难以用硬件实现.存储这些矩阵的困难以及对测量过程的某些物理限制使得在实践中实现CS非常困难.而且,当将任意矩阵与高维的信号矢量相乘时,缺少任何快速矩阵乘法导致计算成本偏高.因此,在CS过程中,如何构建测量矩阵与非线性重构算子是最重要的2个部分.测量矩阵构建得好,则能够用更少的存储空间来对压缩测量值进行存储,提高信号的重建质量.
深度学习是一个新兴领域,可以学习数据多个层次的表达,并已成功用于图像处理任务.深度学习也应用于分布式CS、量化CS和视频CS.在本文中,采用深度学习方法来学习优化测量矩阵和从测量到原始信号的非线性重建过程.为了设计适合于硬件实现的测量,本文采用由{0,1,-1}组成的稀疏矩阵,在所提出的网络架构上施加稀疏性和二元约束.本文方法在图像块上进行训练,学习测量矩阵用于以块为基础获取图像.实验结果表明,高质量的重建可以通过只包含5%非零项{1,-1}的测量来实现.
-
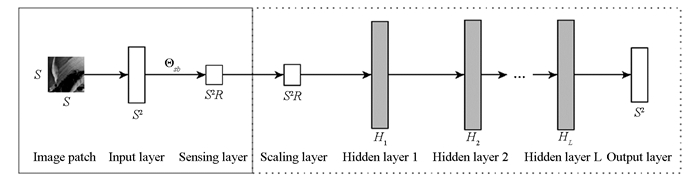
本文算法创新性有2个方面:①提出了一个实现传感层权重的稀疏技术,结合二值化技术,本文方法产生了一个高度稀疏的三元测量矩阵,学习测量可以高效地存储,并允许在采集期间快速计算,也适用于硬件实现. ②简化了深度神经网络中的第一层,对于线性测量矩阵,允许重建模块为非线性以实现重构高性能.网络架构如图 1所示.它由一个传感和重建模块组成.
该网络将大小为n=S2的矢量图作为输入,感测层将n维输入信号x投影到m维域,因此,该层中的单元数为m=S2R,其中0 < R < 1是感测速率.感测层具有对应于测量矩阵Φ的权重Θsb∈{-1,0,+1}n×m,Θsb=ΦT.为了学习一个简单的线性测量矩阵,不在这一层放置偏置和非线性激活功能.
重建模块中的第一层是缩放层,其通过学习因子α线性缩放感测层的输出.该层由m个隐藏单元组成,这些隐藏单元连接到传感层m个隐藏单元的“1-1”,并用于补偿由感测权重二值化引起的损失.然而,在部署时只有测量矩阵被实现在感测设备中,并且学习的缩放因子被保持在重建模块中.缩放层之后是L隐藏层.这些隐藏层将整流线性单元(ReLU)激活功能作为激活函数.输出层是一个线性完全连接层,其大小等于输入维度,重建模块中除缩放层以外的所有层都完全连接,并且之后是批量标准化层.
-
一般网络培训遵循标准的小批量梯度下降法. xi和\[{\mathop x\limits^ \wedge _i}\]分别表示输入信号和重建信号,xi,\[{\mathop x\limits^ \wedge _i}\]∈Rn,n=S2,本文将输入和重建之间的均方误差作为本算法的输入损失函数.
其中,N是样本数量,与传统的小批量梯度下降方法相比,本文算法在传感层的训练中引入了稀疏化和二值化步骤.首先稀疏连续值的感知权重Θ∈Rn×m得到稀疏权重Θs∈Rn×m,保留Θs中前K个最大绝对值的项,其他项置零,将此过程称为top_K_select功能.顶部权重的选择可以按列、按行或在整个矩阵上应用.由于如下所述的缩放层更新涉及感测权重的列式运算符,所以选择以列方式执行top_K_select.
传感层中的每个神经元连接到输入信号中的K=S2γ元素,其中γ是稀疏比.在执行方面,本文构造了一个稀疏的二进制掩码M∈{0,1}n×m,其条目等于1,对应于Θ中最大的权重.稀疏感测权重根据Θs=H(M,Θ),H(·)代表Hadamard乘积.
二值化步骤涉及稀疏连续值权重Θs和稀疏二进制权重Θsb∈{-1,0,+1}n×m的映射.稀疏和二值化步骤都会带来一些损失,出于这个原因,在传感层之后加一个缩放层,具有权重α∈Rm的该层充当稀疏二元化权重Θsb到连续权重Θs的逆映射.因此,缩放层的输出αΘs bTx是ΘTx的近似值,即对应于连续投影ΘT的测量.设θ(j)和θsb(j)分别为Θ和Θsb的j列,θ(j)表示传感层隐藏单元的j列密集连续权重,则可用αjθsb(j)近似θ(j),αj表示缩放因子,对应于缩放权重α的j个值,αj和θsb(j)的值可以通过其均方误差最小值来确定.
对式(5)进行扩展得到
其中,θ(j)Tθ(j)是一个常数,αj是一个正标量,考虑到本文的稀疏性约束,获得最优稀疏二元矢量θsb(j)作为问题的解决方案.
其中,θs(j)是Θs的第j列,supp(·)表示处理矢量的非零条目位置,式(7)的解是包含θs(j)的符号向量.在获得最优θsb(j)后,可以通过使E的导数等于零来求解最佳αj.考虑到θsb(j)Tθsb(j)=K,最佳αj可以由式(8)得到.
经过稀疏和二值化步骤后,Θsb稀疏并且有K个非零项.遵循现有的具有二进制权重的网络训练算法,在前向和后向传播期间使用稀疏二进制权重Θsb.另一方面,在参数更新期间使用高精度的权重Θ,以适应每次更新步骤后的权重的小变化.在训练中,使用损失函数关于Θsb的梯度来更新Θ.应该注意的是,尽管Θsb在{-1,0,+1}中仅包含离散权重,但相对于它的损失梯度仍然位于连续域中. Θt,Θst和Θs bt分别表示连续的,稀疏的和稀疏的二进制测量权重,αt表示缩放层的权重,Wt表示重建权重Wt和θs(j)t表示在第t步的θs(j),则本文提出的稀疏三元测量矩阵训练算法和步骤t中的重建权重算法如表 1所示.算法输入:图像X,权重Θt-1和Wt-1,学习率u,算法输出:损失函数L,更新权重Θt和Wt,稀疏二值权重Θs bt,缩放权重αj.
2.1. 算法网络结构
2.2. 深度神经网络CS
-
为了评估本文所提出的算法,进行了图像恢复实验,第一个测试集采用了ILSVRC2012数据集进行验证,包括用于训练的50 K图像,并在分辨率为256×256的2组测试图像上测试了本文模型.第2个测试集由LabelMe数据集中随机选择的50个图像组成,所有图像在实验中转换为灰度.为了减少计算量,在32×32像素的小图像块中运行了本文实验.
总共随机抽取了500万个图像来组成训练集,在训练期间通过减去平均值并除以标准偏差对输入图像进行预处理.为了避免过度拟合,本文实验在重建模块上采用l2正则化,权重等于0.001.在测试阶段,从每个测试图像中抽取重叠的块,步幅为2个像素,并将最终的图像重建作为块重建的平均值.使用峰值信噪比(Peak Signal to Noise Ratio,PSNR)作为本文方法的评估指标,关于网络架构凭经验将非线性隐层L的数量设置为2,每个都隐藏2 048个单位,因为这种配置在训练时间和重建质量之间产生了良好的平衡. 图 2是训练的部分图像.
首先,尝试不同的稀疏比,使γ=0.1,压缩采样比R取值为[0.1,0.3],表 2中给出了第一组测试集上的平均PSNR值.
由表 2中数据可以得到,由于在测量中保留了来自信号的更多信息,所以整体重建质量在更大的压缩采样比下变得更好.在R=0.25时,对不同稀疏比条件下图像重建性能进行验证,输入图像的大小为32×32,可以得到Θsb∈{-1,0,+1}1024×256,表 3列出了第一组测试集的平均PSNR值.
表 3中数据第1行是γ值,取值从0.001~1,第2行是PSNR值,由此可以得到只有0.1%非零输入(γ=0.001)极其稀疏的测量矩阵可以实现可接受的重建性能.将γ从0.001变化到0.005可显着改善性能,而γ=0.005和γ=0.010之间的差异可忽略不计.在γ=0.050时达到峰值性能,并且在γ为0.100,0.300,1时表现稍差.应该指出,在γ为0.001,0.005的情况下,测量矩阵中分别有256个和1 280个非零项.前者不足以完全覆盖1 024维输入信号,则认为当γ增加到0.005时,这就是性能明显跳跃的原因.
将本文方法与现有方法进行比较,因为本文方法采用深度网络实现CS,因此将与其他深度学习的CS方法[14],例如从文献[14]中选择最好的算法,称为O-NL-SDA算法,以及传统CS方法采用随机三元测量和BP重构进行比较,使用相同的感测速率R=0.25.我们选择γ=0.05的方法,因为它产生最佳的性能,同时产生一个高度稀疏的测量矩阵,表 4中给出了不同算法的重构性能比较.
在第2个测试集中,O-NL-SDA、BP和本文算法的平均PSNR值分别为26.96 dB,21.93 dB和27.61 dB.本文算法具有比使用BP和三元但不稀疏测量的常规CS重建更好的结果.尽管只有5%非零的稀疏三元矩阵,但本文方法在恢复性能方面优于O-NL-SDA.关于重建器的速度,使用前馈神经网络实现的重构器可以比凸优化求解器快几个数量级,不过本文方法可以提供传感机制的便利硬件实现,具有比现有技术更好重建质量的快速重建器. 图 3是对Dog图像的重构效果图.
可以看出,本文方法重建性能优于O-NL-SDA和BP算法.
-
本文提出了一种新的深度神经网络的稀疏测量的CS方法,该方法设计了一种高度稀疏的三元结构矩阵,方便测量过程硬件实现.另外,该方法采用深度神经网络来训练一对测量矩阵和重构算子,优化线性测量过程和非线性重构过程.实验结果表明,对于具有5%非零二进制条目的测量矩阵和利用所提出算法端对端训练的相应重构算子,能够有效实现图像重构,并且重构性能优于O-NL-SDA和BP的压缩感知算法.极其稀疏的测量矩阵,只使用相同算法0.1%非零值的测量矩阵也可以获得较好的重构性能.








 DownLoad:
DownLoad: