-
聚类有效性评价指标是对聚类结果进行优劣判断的依据, 通过比较指标值可以确定最佳聚类划分和最优聚类数[1].对于无先验知识的样本来说, 不同的指标所得到的最优聚类个数可能不同[2-3], 哪种评价指标的K值更具有参考价值是机器学习领域中的热点问题, 许多经典的内部聚类评价指标被先后提出, 诸如CH, IGP, DB, Fr, BWP[4]已被广泛应用, 并取得了较好的效果.但是, 这些指标往往倾向于从整体结构上度量聚类结果的紧致性, 而对各簇之间可能存在紧致性不一致的情况有所忽略, 导致部分指标的应用范围受到一定限制[5].因此, 如何改进或设计出更为合理的评价指标是聚类评价领域的一个重要研究方向.此外, 聚类结果评价除了和有效性指标本身有关, 还与所采用的聚类算法息息相关, 与K-means[6]、K-medoids[7]算法相比, AP算法[8]无需初始化聚类中心, 具有快速、稳定等优点, 尤其在处理大规模数据集时, AP算法的性能是其他传统聚类算法所不能及的.研究表明:AP算法对结构复杂的数据集进行聚类时, 受参数p的影响较大, 聚类数目往往高于实际值[9-11], 因此有必要进一步分析聚类数的范围及合理性.
鉴于上述指标与AP算法在应用中存在的不足, 本文对AP算法进行了改进, 将其聚类区间进一步压缩, 同时, 在对常用内部评价指标对比分析的基础上, 提出了一个新的评价指标, 并结合改进后的AP算法设计了聚类质量评价模型, 采用UCI数据集和KDD CUP99数据集验证了新模型的有效性.
HTML
-
为便于对AP算法、各内部评价指标和本文算法进行描述, 设样本集合X={x1, x2, …, xi, …, xN}, 样本总数为N, l表示样本的特征维度, xi={xi1, xi2, …, xil}, 将样本集划分为K个簇, X={C1, C2, …, CK}, ni为簇Ci的样本个数, c为样本集的均值中心, 簇中心集合V={v1, v2, …, vK}.
-
AP算法是一种近邻之间互传信息的聚类方法[12], 其基本思想是:首先通过计算样本对之间的相似度s构建整个样本集的相似度矩阵S, 再以迭代的方式分别计算出吸引度r和归属度a, 通过判断r与a的和是否满足一定的条件来计算样本成为类代表点的可能性, 以迭代次数达到预设上限或类代表点经多次迭代后不发生变化为算法终止条件[13-14], AP算法的具体执行步骤如下所示:
步骤1:构建相似度矩阵S.使用式(1)计算2个样本xi和xk间的相似度值s(i, k), 进而完成样本集相似度矩阵S的构建.
其中, p(k)表示xk被选作簇中心的倾向性, 该值越大, 意味着xk成为簇中心的可能性越大.
步骤2:传递信息, 更新吸引度r与归属度a.通过迭代循环不断地进行信息传递, 交替更新吸引度与归属度值, 以产生高质量的类代表.其中, r(i, k)表示xk对xi的吸引度, 可以理解为xk适合作为xi的类代表程度, 该值越大, 说明xk作为xi簇中心的几率越大;a(i, k)表示xi对xk的归属度, 用来描述xi选择xk作为其类代表的适合程度, 该值越大, 说明xi将xk视为簇中心的几率越大. r(i, k)和a(i, k)的具体更新方法如式(2)、(3)所示:
由于在上述信息传递过程中, 存在一定的振荡, 因此需要引入阻尼因子λ, 通常λ∈[0, 1), 其作用是校正前后2次迭代的r(i, k)和a(i, k), λ越大矩阵更新速度越慢, 迭代过程愈加平稳, 消除震荡的效果越好, 设迭代次数为t, 经校正的信息传递过程如式(4)、(5)所示:
其中, r(i, k)t和a(i, k)t分别表示第t次迭代的吸引度和归属度, r(i, k)t+1和a(i, k)t+1分别表示第t+1次迭代的吸引度和归属度.
步骤3:确定类代表点.选择满足吸引度r(i, k)和归属度a(i, k)之和最大的样本xk作为xi的类代表点, k所满足的条件如式(6)所示:
从上述公式可知, 偏向参数p将会在式(2)计算吸引度r中出现, 当p值增大时, r和a也随之增大, 因此候选点成为簇中心的可能性增大.当候选点数量较多且其p值较大时, 将有更多的候选点倾向于成为真正的簇中心, 而p值的选取目前尚无成熟的理论依据, 这样就导致了该算法大多以局部最优或近似全局最优作为最终结果[15].取相似度的中位数作为p值得到的聚类数往往大于正确类数, 这虽然具备一定的参考价值, 但精度依旧不足, 因此需要进一步分析聚类数的合理性, 以达到更理想的效果.此外, 当样本数量过大时, AP算法易出现存储空间不足或者聚类时间过长的问题, 尤其对于非团状的数据集, AP算法往往产生较多的局部聚类.为了解决这一问题, 文献[16]使用BWP指标对AP算法得到的全部聚类结果进行评价, 得出最佳聚类数, 但是由于聚类上限值过大, 算法耗时长的问题依旧未得到有效解决.文献[17]将merge过程融入AP算法中, 将簇间距离最小值小于整个数据集平均距离的2个簇进行合并, 提高了算法的运算速度, 解决了对非团状数据聚类效果不佳的问题.但是由于该算法采用的是簇间最小距离, 因此, 在合并过程中存在将相似度较低的样本数据聚在一类的隐患.
-
内部评价指标是指在不涉及任何外部信息, 仅依赖数据集自身特征和度量值的条件下, 通过计算簇内、簇间或整体相似度来评价聚类效果的优劣.理想的聚类效果是簇内紧密且簇间分离, 已有内部评价指标[18-22]的主要思想是通过簇内距离、簇间距离或样本集的平均距离的某种形式的比值来度量的, 常见的内部评价指标及其特点分析如下所示:
1) DB指标(Davies-Bouldin Index)[18]
DB指标首先将相邻2簇的簇中各样本与簇中心的平均距离之和作为簇内距离, 将相邻2个簇中心的距离作为簇间距离, 然后取二者比值的最大值作为该簇的相似度, 最后对所有簇的相似度取平均值得到样本集的DB指标.可以看出, 该指标越小说明各簇间的相似度越低, 对应的聚类结果越理想, 该指标常用于评价“簇内紧凑, 簇间远离”的数据集.但当数据集的重叠度较大, 如遇到环状分布数据时, 由于各簇中心重叠, 因此DB指标很难对聚类结果形成有效评价.
2) CH指标(Calinski-Harabasz)[19]
CH指标将各簇中心点与样本集的均值中心的距离平方和作为数据集的分离度, 将簇中各点与簇中心的距离平方和作为簇内的紧密度, 将分离度与紧密度的比值视为最终指标.该指标越大表示各簇之间分散程度越高, 簇内越紧密, 聚类结果越优.从CH指标的函数表达式可以看出, 当聚类数趋近于样本容量N时, 各样本自成一簇, 簇中心即为各样本自身, 此时簇内距离和约等于0, 分母为极小值, CH指标将趋于最大, 此时的聚类评价结果无实际意义.
3) Fr指标[20]
针对CH指标中簇内距离和有可能趋于0的问题, 文献[10]对其进行了改进, 在原指标的基础上乘以因子lg K, 来调节当K值趋于N时CH出现极值的情况.一般情况下K≥2, lg K大于0, 因此Fr指标的变化趋势与CH指标相类似, 即该指标值越大, 聚类质量越好.
Dunn指标用簇间距离与簇内距离的比值表示, 簇间距离是任意2个不同簇的样本间的最小距离, 簇内距离用最大簇的“直径”表示(簇内两个样本间的最大距离), 可以看出Dunn指标越大, 意味着簇间距离越大, 同时簇内距离越小, 说明聚类质量越好.事实上, Dunn指标跟CH指标一样, 都不适用于散点状数据, 即当簇内样本趋于1时, 簇内距离接近于0, 指标值最大, 意味着聚类结果最佳, 但此时的聚类结果明显与真实分布有较大偏差.此外, 当数据成环状或长条状分布时, 由于簇间距离很小, 而簇内最大距离却很大时, 也会出现聚类结果理想, 但评价指标很低的情况.另一方面, 由于Dunn采用了聚类结果中所有簇类的最大直径, 而忽略了不同簇间直径的差异性, 因此, 在一定程度上降低了聚类评价的准确度.
5) IGP指标(In-Group Proportion)[22]
IGP将2个距离最近的样本划分到同一簇的比值作为评判聚类质量的标准, 其依据是在对某样本进行聚类划分时, 与该样本所属同一簇的其它对象应该与该样本的相似度最高.即
其中igp(i, X)表示数据集X中的第i类的指标值, jN是距离样本j最近的样本, ClassX(j)表示数据集X中的第j个样本所属的类别.由于IGP仅关注最近邻的一致性, 当K值逐渐增加时, 该指标会不断减少, 在实际使用中, 使用该指标得到的聚类个数往往少于真实个数[23].
1.1. AP算法
1.2. 内部评价指标
-
聚类质量评价模型由改进的AP算法和新内部评价指标两部分构成, 鉴于AP算法对非团状数据的聚类个数远大于真实的聚类数目, 以及上述常用内部评价指标的不足, 本文对二者分别进行了改进.
-
本文在文献[24]的基础上, 对AP算法得到的初步聚类结果按相似度进行合并, 通过减小聚类上限kmax, 将聚类区间压缩至合理范围, 以提高聚类精度.基本思路是:首先使用AP算法对样本集聚类, 再计算任意两簇间最远边界点的距离与样本集平均距离的比值α, α表示相邻两簇与样本集在空间结构上的相对关系, 该值越小意味着2个簇的相对相似度越高, 在遍历完全部簇之后, 若最小α在指定阈值范围内, 则将两簇合二为一, 否则, 保持不变, 新算法的定义和公式如下所示:
定义1 空间任意两点间的欧氏距离定义为
其中, i=1, 2, …, N;j=1, 2, …, N;l表示样本的特征维度.
定义2 样本集的平均距离定义为:各数据对象间的距离总和与样本对数量的比值.
其中, AN2表示从样本集X中任意选取2个样本的排列次数.
定义3 任意两簇之间的距离定义为:2个簇间最远边界点的距离.
其中, xt和xu表示簇Ci和Cj相距最远的2个样本.
定义4 簇间相似度定义为:簇间距离与样本集平均距离的比值.
定义5 如果簇间相似度α在给定阈值范围w内, 则将两簇合并, 否则保持不变.
其中, 阈值范围w可由用户自行设定, 其默认值为[1, 1.5].
-
在对无先验知识样本的聚类结果进行评价时, 通常将簇内紧密, 簇间分离作为内部评价的重要标准, 若将各簇中心点间的距离作为簇间距离, 可能会出现因簇中心重叠而导致聚类评价结果失效等问题.本文在XB指标[25]的基础上进行了优化, 用分属2个不同簇的全部样本对的距离之和的最小值表示簇间距离, 通过增强簇间的平均相似性, 削弱噪声数据的影响, 避免数据成环状或长条状分布时指标失效, 新指标Improve-XB(以下简称IXB)的定义及公式如下:
定义6 簇内紧密度(Compactness)定义为:簇内全部样本与所属簇中心的距离之和.
其中, x表示簇Ci内的样本, vi是簇Ci的中心, K表示样本集的聚类个数.
定义7 簇间分离度(Separation)定义为:两簇间全部样本对的距离之和的最小值.
其中, xt和xu分别表示簇Ci和簇Cj中的任意2个样本.
定义8 IXB指标定义为:簇内紧密度与簇间分离度的比值与其倒数之和.
定义9 最优聚类数Kopt定义为:IXB(K)取最大值时的聚类数目.
其中, K∈[2, Kmax], Kmax由改进的AP算法给出.
从定义8可以看出:IXB指标中的Sep/Com随着聚类数K的增加而递增, 而Com/Sep则反之, IXB通过制衡簇内紧密度和簇间分离度之间的关系, 确保了最优聚类的划分, 该值越大, 说明聚类质量越好.
-
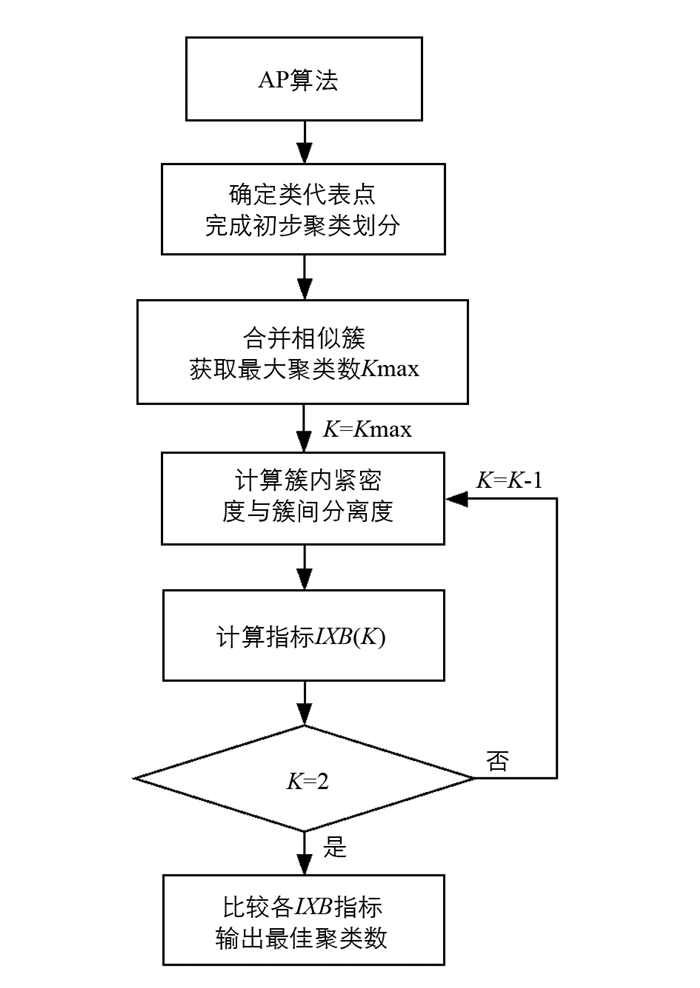
将改进的AP算法与IXB指标相结合, 构建的聚类质量评价(Cluster Quality Evaluation, 以下简称CQE)模型如图 1所示, 模型的实施分为3个环节, 具体描述如下:
1.确定类代表点
a) 使用式(1)计算各样本对间的相似度s, 进而得到样本集的相似度矩阵S.
b) 设置阻尼因子λ, 迭代次数t, 使用式(2)、式(3)迭代更新吸引度r与归属度a, 使用式(4)、式(5)对吸引度和归属度进行校正, 消除震荡.
c) 根据式(6)将吸引度与归属度之和最大的候选点作为类代表点, 重复执行步骤b, 完成全部簇代表点的选取, 最后将非代表点样本划分至相应簇中.
2.获取最大聚类数Kmax
a) 根据式(13)、式(14)计算样本集的平均距离.
b) 根据式(13)、式(15)计算任意两簇的最远边界点间的距离, 并将该值作为这两簇的簇间距离, 重复执行本步骤, 得到各簇间的距离矩阵.
c) 使用式(16)计算各簇间的相似度, 设置阈值范围w, 根据式(17)对满足条件的簇进行合并, 实现簇更新.
d) 重复执行步骤b, c, 更新各簇间的相似度, 直至相似度值超出给定的阈值范围, 得到最大聚类数Kmax.至此, 簇更新结束.
3.确定最优聚类数Kopt
a) 将最大聚类数Kmax作为K的初始值.
b) 使用式(18)、(19)分别计算各簇的簇内紧密度Com与簇间分离度Sep, 使用式(20)计算IXB指标.
c) 令K=K-1, 重复步骤b, 完成K∈[2, Kmax]范围内的IXB指标的计算.
d) 根据式(21), 将IXB取最大值时的K值作为最优聚类数Kopt输出.
2.1. 改进AP算法
2.2. 聚类有效性指标Improve-XB
2.3. 聚类质量评价模型描述
-
实验分为有效性测试和模型应用2个部分:首先, 使用改进的AP算法依次结合IXB和其他5个评价指标对UCI数据集(表 1)进行聚类数对比测试, 目的是验证模型的有效性;其次, 将CQE模型应用于数据集KDD CUP99, 从检测率、分类正确率、漏报率3个方面验证其实用性.本文实验环境:Intel(R) Core(TM) i3-3240, CPU @3.40GHz, 8G内存, Win10专业版, 实验平台Matlab 2011b.
-
在该测试环节中, 使用DB, CH, Fr, DVI和IGP 5个内部评价指标与本文的IXB指标进行对比, 对比结果如表 2所示.
观察表 2可知, IXB在5个UCI数据集上的聚类数正确率为80%, 而DB, CH, Fr, DVI和IGP指标依次为20%, 60%, 60%, 40%, 40%, IXB指标的聚类数正确率明显高于其他5种指标.
-
本实验环节选取KDD CUP99[26-27]训练集中的12 320条记录作为训练数据, 从corrected数据集中随机选取10 520条数据分成4组, 作为测试集用于检验模型的性能.在数据预处理方面, 首先使用One-hot编码完成字符数据的格式转换, 再将数据集的41个特征降维至14个[28], 经归一化处理后的样本集描述如表 3.
-
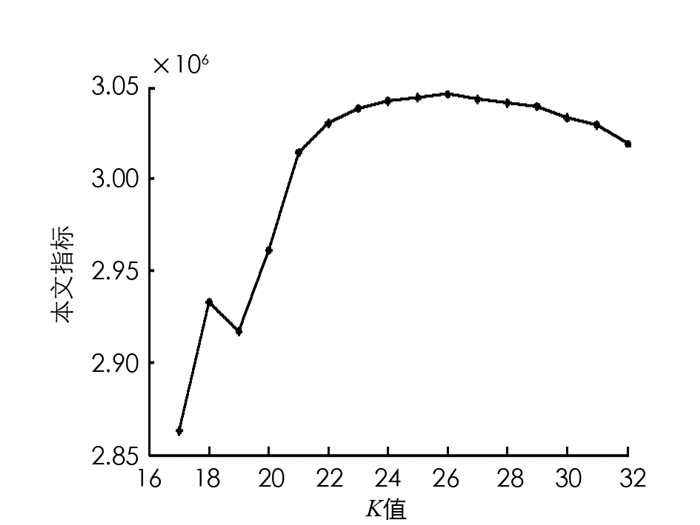
设定阈值范围w=[1, 1.5], 阻尼因子为0.9, 最大迭代次数为1 000次, 执行改进AP算法后得出训练集的最大聚类数Kmax=32, 使用CQE模型得出的IXB指标结果如图 2所示.可以看出, 随着K值的不断增大, IXB呈现上升趋势, 当23≤K≤25时, IXB逐渐趋于平稳;当K=26时, IXB达到极大值, 此后随着K值的再次增大, IXB缓慢下降;当K=29时, 下降幅度明显增加.需要特别指出的是, 当K=18时, IXB指标发生了异常变化, 通过观察表 4中的Com、Sep以及IXB指标值可知, Com18<Com19, 查询K=18和K=19时训练集的聚类结果发现, 前者对异常数据的分类正确率为78%, 后者为76%, 因此, 前者的簇内紧致程度优于后者, 而当K=19时, 虽然簇间分离度有所增加(Sep18=1 524 019 748, Sep19=1 524 738 937), 但其增幅较小, 所以IXB(18)>IXB(19).
-
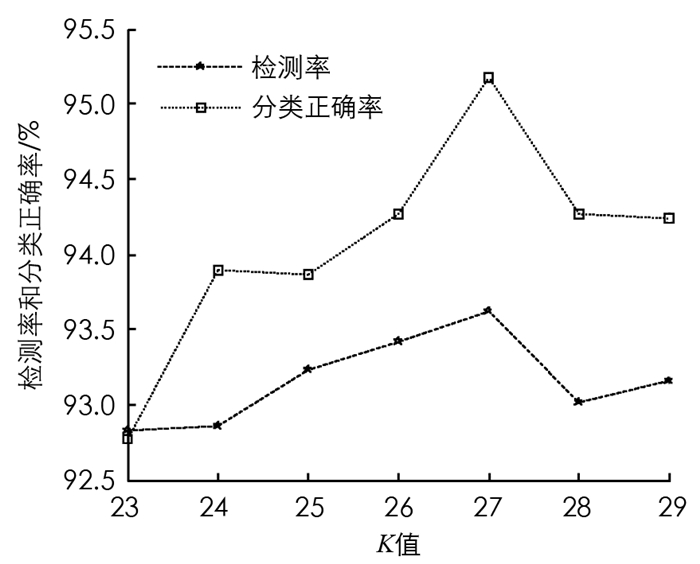
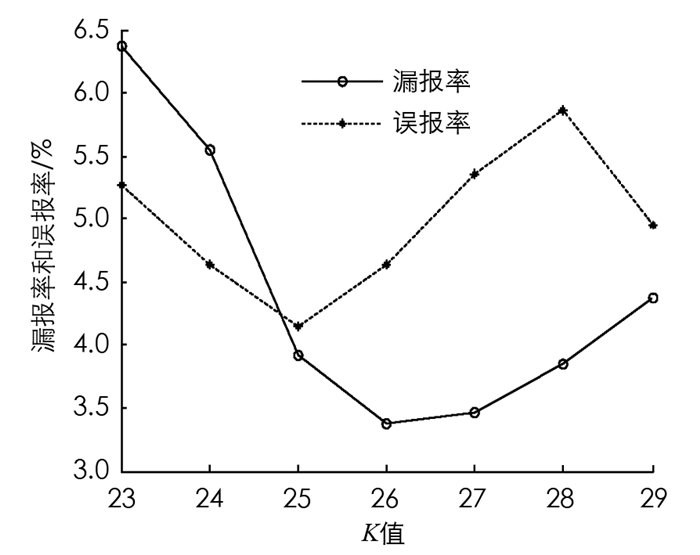
为了验证通过IXB指标得出的最优K值是否有效, 即K取最优值时的各项入侵检测指标是否有效, 本文将图 2中IXB缓慢上升至峰值, 再从峰值缓慢下降这一阶段所对应的多个连续K值定义为最优聚类数范围, 即Kopt∈[23, 29], 使用4组测试集对该范围内的入侵检测指标分别进行了验证, 结果如表 5所示.取平均值后的折线图如图 3、图 4所示, 可以看出, 当聚类数为27时, 入侵检测率和正确分类率同时达到最大值, 分别是93.62%, 95.17%;当聚类数为26时, 漏报率达到最小, 为3.37%;当聚类数为25时, 误报率达到最小, 为4.14%.
-
为进一步验证IXB指标的普适性, 同时也为了将CQE模型和其他算法的聚类质量进行横向比较, 本环节将K-means、文献[18]和文献[19]算法与IXB指标相结合, 在Kopt∈[23, 29]这一区间内对入侵检测指标进行了对比测试.观察表 6和表 7的对比结果可知, 结合了IXB指标的其他3种算法的检测率和分类正确率在K={25, 26, 27}时可得到最大值, CQE模型的检测率和分类正确率在整个区间内全部优于其他3种算法, 其最大检测率为93.62%, 最大分类正确率为95.17%.
由表 8可看出, 在漏报率方面, 除了个别结果, 本文算法均优于其他3种算法, 其最小漏报率为3.37%.
由表 9的误报率可看出, CQE模型在K={24, 25, 26}时的误报率低于其他3种算法, 其他范围内CQE模型的误报率略高, 但总体上低于其他3种算法的平均值.
从本环节的对比测试可以看出, IXB指标具有良好的普适性, 相比于其他3种算法, CQE模型的聚类结果更为理想, 能够以较小的误报率代价, 提高入侵检测率和分类正确率, 降低了漏报率, 在整体性能上取得了较好的效果.
3.1. CQE模型的有效性测试
3.2. CQE模型在KDD CUP99中的应用
3.2.1. IXB指标与K值的关系
3.2.2. 最优聚类数范围内的各检测指标
3.2.3. CQE模型和其他算法的对比测试
-
本文提出了一种改进的AP聚类算法, 以簇间相似度为参考依据, 通过循环合并相似簇的方式, 将聚类区间压缩至较小范围, 解决了AP算法对结构复杂的数据集进行聚类时出现的局部聚类过多、精准度低的问题;改进了XB评价指标, 通过计算不同簇间样本对平均距离的方法削弱噪声数据影响, 增强簇间的平均相似性, 解决了因中心点过于紧密, 而导致指标无效的问题.实验结果表明, 由改进AP算法和IXB指标构建的CQE模型可以给出精准的最优聚类数范围, 但是在如何设定阈值方面, 本文暂时无法给出较为成熟的理论依据.下一步工作将深入研究阈值范围的设定与样本集的关系, 使得CQE模型的功能更加完善, 具有更广的应用范围.






 DownLoad:
DownLoad: