-
随着数据通信和互联网的进步, 数字图像出现了爆炸性增长[1], 同时也伴随着较为严重的信息安全问题[2].图像水印技术作为一种信息隐秘技术, 可以解决图像传输过程中存在的信息安全问题[3-6].
文献[7]的研究结果指出, 水印嵌入强度会影响水印图像的密钥信息隐秘性与稳健性, 因此, 需要对其进行优化, 确定一个最佳的嵌入强度, 以平衡不可感知性与鲁棒性.为此, 根据文献[7]的思想, 本文利用人工蜂群机制, 提出了基于离散余弦变换DCT(Discrete Cosine Transform)与最优嵌入强度预测的鲁棒图像水印算法.通过引入离散余弦变换来分解宿主图像子块, 从中选择一个参考系数和4个嵌入系数.根据水印图像的质量与不同攻击类型的鲁棒性来构建适应度函数, 通过迭代人工蜂群算法来对样本进行训练, 以获取最优嵌入强度值.根据该优化的嵌入强度构建水印嵌入方法, 将水印信息隐藏到宿主图像中, 使其可以较好地兼顾视觉隐秘性与抗攻击能力.最后, 对所提方案的信息隐秘性与抗几何变换能力实施了测试.
HTML
-
对于尺寸为L×H的图像f(x, y), 可以利用两个连续的1D-DCT来计算其2D-DCT[8]:
其中: C(u, v)是2D-DCT变换系数; x, y是f(x, y)中像素点的位置; L×H代表图像尺寸; u, v是像素点(x, y)在DCT域内对应的位置数; S(u), S(v)都是C(u, v)的核变换
通常, 式(1)主要是用于将图像分割为8×8后的非重叠子块, 从而输出对应的低频与高频子带.为了重构图像, 需要用到式(1)的逆变换, 其模型为[8]:
初始图像f(x, y)被式(1)变换后, 其大部分能量主要集中在低频系数上, 充分反映载体图像的背景, 有效避免了显著性目标, 能够改善其隐秘性, 对JPEG压缩等几何变换具有良好的稳健性[9].所以, 在所提水印方案中, 主要是择取宿主图像对应的低频系数来实现水印嵌入.以图 1(a)为样本, 对其实施DCT处理后, 输出数据见图 1(b).
-
人工蜂群(ABC, artificial bee colony)是一种有效的自然启发优化技术, 它是一种基于群体的优化算法[10-11]. ABC算法主要是通过将蜜蜂群体分成3组来执行:
1) 受雇蜜蜂.它们从不同的来源收集食物, 然后返回蜂房储存食物并表演摇摆舞, 以表明它们访问过的食物的质量.
2) 观察蜜蜂.它们观看舞会, 以了解高品质的食物来源, 并据此告知受雇的蜜蜂要探索的邻近来源.
3) 侦查蜜蜂.它们主要是随机探索新的食物来源.
ABC算法主要是通过引入上述3个群体来搜索最优或近似最优解, 主要过程如下:
Step 1:初始化.随机产生一个大小为NS的蜂源, 每个目标X均位于Xmin=(Xmin, 1, Xmin, 2, …, Xmin, Ds)与Xmax=(Xmax, 1, Xmax, 2, …, Xmax, Ds)之间, 其中, Ds是解空间的维度.则蜂源的产生函数如下:
其中: i=1, 2, …, NS是蜂源的数量; j=1, 2, …, Ds是解的维度; r(0, 1)是一个随机数.
Step 2:雇佣蜂阶段.雇佣蜂更新它们的位置(解)以产生新的种群.每个解Xi是通过如下函数修改其邻近元素Xi, j来更新的:
其中: yi, j是更新位置Yi中的第j个元素; φi, j∈[-1, 1]是一个随机数; k=1, 2, …, NS是第k个蜂源.为了保持更新的有效性, 需要保持k≠i, 并根据各自对应的适应度函数来比较Xi与Yi, 若Yi的适应度值大于Xi, 则用Yi替代Xi.
Step 3:观察蜂阶段.在该过程中, 每个观察蜂通过任选一个解, 使用式(5)来更新, 并根据概率值来确定一个最优解[10]
其中: Pi是第i个解对应的选择概率; f(si)是第i个解的适应度.
Step 4:侦查蜂阶段.侦察蜂随机搜索新的解.在ABC算法中, 定义了一个值, 名为“Trials”.所有的更新解均有一个初始的Trials值, 为零.如果一个解的Trials值超过了预设值(称为“Limits”), 则利用式(4)产生的随机解来替代它.
Step 5:检查算法迭代终止条件. ABC算法是一种迭代方法, 它不断重复前面Step 2-Step 4, 直到满足停止准则.一般而言, 通过设置一个表示最大迭代次数的预定值来定义停止准则.
-
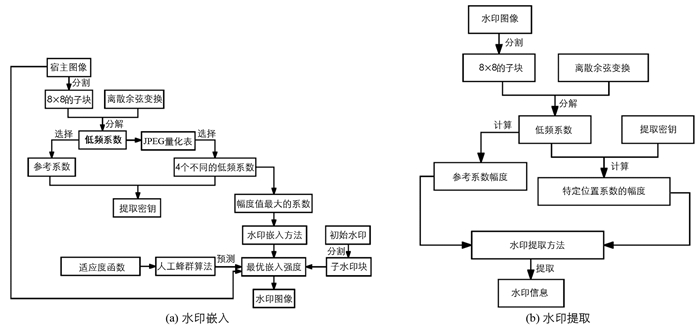
基于离散余弦变换与最优嵌入强度预测的鲁棒图像水印算法示意图见图 2.将安全密钥融入到水印检测阶段, 可增强系统的安全性.基于离散余弦变换与最优嵌入强度预测的鲁棒图像水印算法主要分为两个部分, 分别见图 2(a)和图 2(b).选择离散余弦变换后的低频系数可有效增强水印系统的不可感知性; 利用不同攻击类型的鲁棒性来构建人工蜂群算法的适应度函数, 通过对其迭代, 以预测最优嵌入强度值, 从而设计水印嵌入机制, 可较好地平衡水印隐秘性与抗几何变换能力. 最后, 借助水印检测方案来恢复密钥数据.
-
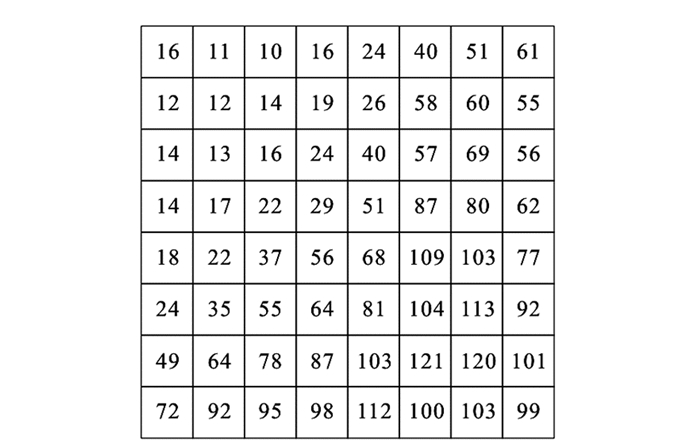
1) 令I={f(x, y), 0≤x < M, 0≤y < N}是大小为M×N的宿主图像, 并将其分割为若干个8×8的非重叠子块, 从而得到图 3所示JPEG量化表;
2) 利用“1离散余弦变换”章节的分解过程, 处理每个子块
利用式(7)处理所有的子块, 可输出对应的低频子带与高频子带.为了便于描述, 令低频子带的系数为C={C1, C2, …, Cz}, 其中z是低频系数的数量.
3) 从C={C1, C2, …, Cz}任意选择一个系数作为参考系数Cref(一般位于左上角处); 再根据JPEG量化表(图 3), 从C={C1, C2, …, Cz}中确定出与Cref具有相近值的4个不同的系数C1, C2, C3, C4;
4) 从C1, C2, C3, C4中选择一个与Cref最为接近的系数
其中: Cw是系数; |·|是求绝对值运算.
5) 记录选择系数Cw的位置, 将其视为选择密钥;
6) 从系数Cref与Cw中确定出最大的幅度值Vmax:
7) 根据Vmax把子水印隐藏到参考系数和选择系数中:
其中: |Cref|*与|Cw|*是嵌入水印后的参考系数与选择系数; α是嵌入强度, 主要通过优化技术来预测其最佳值; I()是指示函数, 其值只有“0”和“1”, 当输入条件wm, n=1时, 则I(wm, n=1)=1.
8) 利用|Cref|*与|Cw|*替代宿主图像中对应位置的系数, 形成水印子块的DCT系数:
其中: (i, j)Cw是选择系数的位置; (i, j)Cref是参考系数的位置.
9) 利用DCT逆变换, 将水印系数转换到空域, 输出水印子块图像.
-
1) 令水印图像为Iw, 并将其分割为一系列的8×8的非重叠子块;
2) 借助DCT方法对每个水印图像的子块实施分解, 输出低频系数:
3) 计算水印子块图像中参考系数的幅度值:
4) 根据水印过程中存储的密钥, 选择位于(i, j)Cw处的系数;
5) 再计算选择系数的幅度值:
6) 借助步骤5)的幅度值, 构建水印检测函数, 以恢复水印内容:
7) 利用步骤1)-步骤6)处理所有的水印子块, 以提取完整的水印信息.
3.1. 水印嵌入
3.2. 水印检测
-
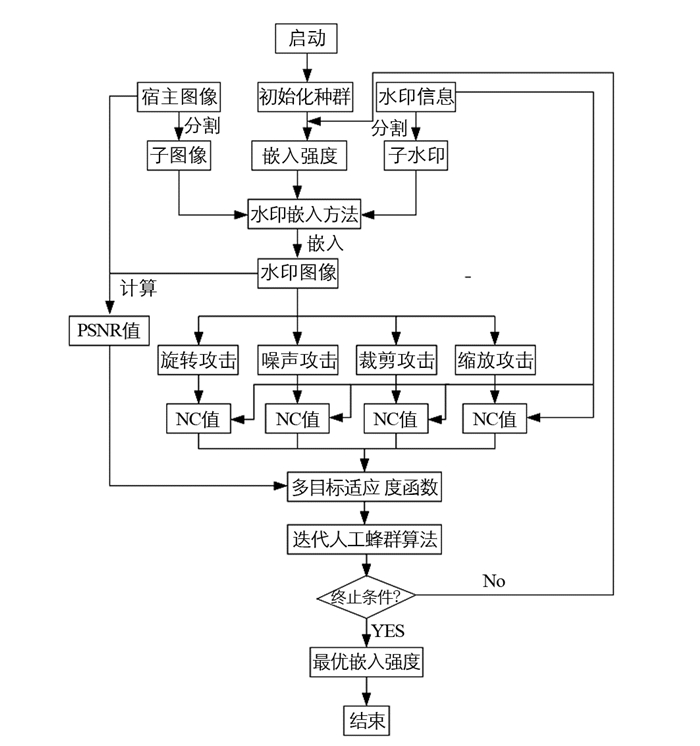
一般而言, 为了增强水印系统的抗攻击能力, 通常会取较大的α值; 然而, 取较大的α值会削弱其不可感知性[7].因此, 为了最大程度地平衡水印图像的不可感知性与鲁棒性, 本文利用人工蜂群算法ABC[11]来预测一个最优的嵌入强度, 其过程见图 4.由图 4发现, 本文主要是利用峰值信噪比[12]PSNR(peak signal noise ratio)与归一化相关系数(normalized correlation-coefficient)[13]NQ来建立ABC算法的适应度函数.其中, PSNR是反映水印图像质量优劣的经典指标, 其值越大, 说明其水印不可感知性越好, 其计算模型为[12]:
其中: PPSNR为PSNR值; I, I′分别是宿主目标与水印结果; n是图像的高度或宽度; (i, j)是像素坐标.
NQ是反映水印系统鲁棒性的经典指标, 其值越大, 表明在几何内容操作下所获取的水印与初始水印更加接近, 其计算公式
根据PSNR与NQ值, 建立人工蜂群算法的适应度函数:
其中q代表几何攻击类型的种类, 在本文中, 取q=4. Qi代表初始水印与在第i种几何攻击下的复原水印之间的归一化相关系数值.
令宿主图像、水印信息分别为I与W, 则水印嵌入强度的优化过程为:
1) 令宿主子图像为Isub, 子水印为wsub, 若Isub的尺寸是Msub×Nsub, 则wsub的尺寸Mw-sub×Nw-sub的计算公式为:
2) 将所有的宿主子图像Isub视为ABC算法的初始蜂源, 用于嵌入水印信息, 并设置最大迭代次数为Tmax, 初始化T=0;
3) 随机选择一个蜂源与一个嵌入强度, 根据“3.1水印嵌入”章节, 将水印信息隐藏到宿主子图像Isub, 形成水印图像, 根据式(16), 计算其与初始宿主子图像之间的PSNR值; 再从水印结果中恢复密钥内容, 并借助式(17), 计算其与源子水印之间的NQ值; 同时, 基于式(18)计算此时的适应度函数;
4) 雇佣蜂利用式(4)来更新子图像Isub对应的蜂源(嵌入强度), 并根据步骤2), 计算不同嵌入强度对应的适应度函数值;
5) 利用式(18)替代式(6)中的适应度f(si), 此时, 侦查蜂利用式(6)来获取蜂源(嵌入强度)的选择概率Pi;
6) 随后, 侦查蜂基于贪婪策略[14]来更新全局最优蜂源;
7) 侦查蜂根据步骤5)得到的Pi确定物源, 且利用式(5)在其领域搜索, 以输出新的蜂源, 并计算其对应的适应度函数值;
8) 如果蜂源经过L次更新保持不变, 则将其丢弃; 否则, 用新的蜂源来替代它;
9) 记录此时的最优蜂源;
10) 判断是否符合迭代终止条件, 如果达到Tmax次, 则输出最优嵌入强度; 反之, 则继续执行步骤4).
对于所有的宿主子图像, 利用上述过程来预测其对应的最优嵌入强度, 以此完成水印信息的隐藏, 最大程度地改善水印图像的视觉隐秘性与抗几何攻击能力, 并将这些嵌入强度组合成一个集合Optimal_α={α1, α2, …αv},
$v=\frac{M \times N}{8 \times 8}$ .
-
将本文算法与文献[6-7]算法进行对比实验.不失一般性, 从USC-SIPI数据库中任选2幅图像, 将二者视为宿主目标, 见图 5(a)-5(b), 大小都是256×256;将图 5(c)-5(d)作为源水印, 尺寸均为64×64.实验参数为: T=0, L=8, Tmax=600, NS=100;观察蜂数量为50个、雇佣蜂数量为50个、嵌入强度α∈[3, 15].
-
利用所提方法与文献[6]、文献[7]的嵌入过程, 将图 5(c)-5(d)分别隐藏到宿主图像(图 5(a)-5(b))中, 形成的水印图像见图 6, 7.由测试结果发现, 3种方案所输出的水印图像都具备良好的视觉不可感知性, 其与初始宿主图像几乎一模一样, 难以直接从中获取有关水印的任何信息.
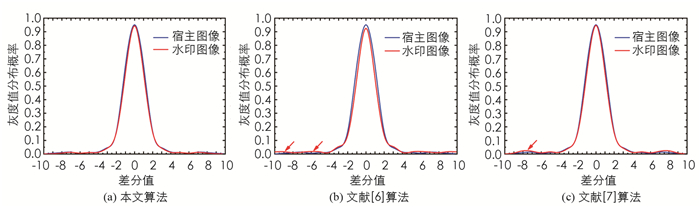
利用人眼主观感觉难以反映技术与文献[6]、文献[7]的水印隐秘性的差异, 因此, 本文借助经典的灰度分布差分图[4]进行客观评价.通常, 若水印图像与宿主图像的灰度分布拟合度越高, 意味着此技术的不可感知性越好.在此次试验中, 将图 7(a), 7(c)-7(e)作为样本, 统计了宿主图像与3种技术所获取的水印图像之间的差分图, 形成的灰度分布见图 8; 又依据式(16)得到了3种技术的峰值信噪比[12]PSNR, 数据见表 1.由图 8可知:本文算法形成的水印图像和宿主图像之间的灰度分布很接近, 几乎没有起伏效应; 文献[7]算法也呈现出理想的差分曲线分布, 灰度拟合情况较好; 文献[6]方法的差分图不佳, 与宿主图像的灰度分布拟合偏差较大, 有明显的起伏效应, 这种灰度分布起伏容易被攻击者发现, 使其不可感知性有待提高.由表 1可知:本文算法得到的PSNR值最大, 约为44.78 dB; 文献[7]算法的PSNR值为43.19, 与本文算法较为接近; 文献[6]方法的PSNR值最小, 约为40.56 dB.主要原因是本文算法利用了DCT机制来分解宿主子图像, 从每个子块中选择低频系数作为嵌入位置, 使得嵌入水印对宿主图像修改范围较小, 且引入了人工蜂群机制来优化嵌入强度, 根据该优化值将水印信息隐藏到DCT系数中, 最大程度地平衡了视觉隐秘性与鲁棒性, 使其很好地保持了宿主图像的灰度分布特征, 因此, 本文算法具有更高的视觉不可感知性.文献[7]技术则是利用离散小波变换来分解宿主子图像, 通过SIFT方法来提取每个子图像的特征点, 并将这些特征点作为嵌入位置, 使其对宿主图像的修改程度较小, 而且利用了粒子群算法来优化其嵌入强度, 较好地兼顾了不可感知性与鲁棒性.但是, 该技术是将整个子块的SIFT特征点作为嵌入位置, 对宿主图像的修改范围要大于本文算法, 故其不可感知性略低.而文献[6]技术则是利用提升小波变换与奇异值分解来实现水印嵌入, 将宿主图像的HL子带作为嵌入位置, 对宿主图像的修改范围较大, 而且嵌入强度主要是一个经验固定值, 故其不可感知性更低.
-
把图 7(c)-7(e)当作对象, 施加表 2所示的几何攻击, 形成一系列的篡改样本.随后, 基于本文方法、文献[6]与文献[7]的水印检测方法, 从这些篡改样本中提取水印, 并根据式(17)相应的归一化系数NQ和位正确率BCR(Bit Correct Ratio)来量化鲁棒性. BCR的计算公式为
其中: W(i, j)是初始水印; W′(i, j)是提取水印; ⊕是XOR算子; ()是NOT算子.
表 3显示了本文算法与文献[6]、文献[7]算法所提取的水印与初始水印之间的NQ与B值.由表 3数据发现, 当水印图像遭受几何变换攻击时, 3种技术所提取的水印质量都存在失真, 鲁棒性由强到弱依次为文献[6]算法、本文算法、文献[7]算法.主要是因为文献[6]算法利用SVM方法设计一种几何校正方法, 在水印提取前, 对遭遇几何攻击的水印图像实施变换参数的预测, 并根据预测结果对攻击水印图像完成校正, 使其具有更高的鲁棒性, 所复原水印具有更好的质量.而本文算法则是利用人工蜂群算法对遭遇多种几何攻击的水印图像进行训练, 以预测最优的嵌入强度, 以此来完成水印嵌入, 最大程度地改善水印系统的鲁棒性.文献[7]算法虽然也利用了粒子群算法来预测最优的嵌入强度, 利用优化后的嵌入强度来获取水印图像, 但是此技术采用的SIFT方法是依赖强度梯度检测的宿主图像特征点来实施水印嵌入, 不能描述图像的非纹理区域的特征, 使得鲁棒性较弱.
-
令载体的大小为M×N, 根据所提算法的过程可知, 其水印嵌入的复杂度主要集中在离散余弦变换DCT处理、JPEG量化以及人工蜂群算法的3个过程.对于大小为M×N图像, 将其分割为8×8的子块, 总共含有(M×N)/64个子块.利用DCT来分解每个子块, 对于其相应的复杂度为o[(M×N)/64]. JPEG量化的复杂度为o(z), z为低频系数的数量.另外, 人工蜂群算法的复杂度为o(Tmax×(M×N)2/642), 其中Tmax为迭代次数.因此, 所提算法的总复杂度为o[(M×N)/64+z+Tmax×(M×N)2/642].
文献[6]的水印嵌入复杂度主要在于小波变换处理、奇异值分解以及支持向量机的训练, 其中, 小波变换的复杂度为o[(M×N)lg(M×N)], 奇异值分解的复杂度为o(1 024 m3), 其中m为每个子块的奇异值数量. SVM的复杂度为o(4a2), a为样本数量.因此, 文献[6]的总复杂度为o[(M×N)lg(M×N)+ 1 024m3+4a2].
文献[7]的水印嵌入复杂度主要集中在SIFT特征点检测、奇异值分解、水印信息的离散小波变换处理以及粒子群算法的优化等4个过程, 其中: SIFT算子的复杂度为o(128n), n为特征点数量.奇异值分解的复杂度为o(4 m3), m为每个子块的奇异值数量.水印的离散小波变换处理复杂度为o[(k×h)lg(k×h)], k×h为水印图像的尺寸.粒子群算法的复杂度为o(4Ts2), T为迭代次数, s为粒子群数量.因此, 文献[7]的总复杂度为o(128n+4m3+(k×h)lg(k×h)+ 4Ts2).
根据上述分析可知, 文献[7]的复杂度最低, 效率最高.而本文算法的复杂度由于采用了人工蜂群算法, 复杂度最高.
5.1. 不可感知性的测试分析
5.2. 鲁棒性测试
5.3. 算法复杂度分析
-
为了较好地平衡水印图像的视觉隐秘性与抗几何攻击能力, 本文提出了基于离散余弦变换与最优嵌入强度预测的鲁棒图像水印算法.在嵌入过程中, 利用离散余弦变换方法来处理宿主子图像, 从中确定出合适的低频系数作为嵌入位置.并基于峰值信噪比与不同类型攻击下的归一化相关系数来建立适应度函数, 通过执行人工蜂群机制, 对每个子图像及其相应的子水印进行水印嵌入强度的优化预测.根据优化的嵌入强度, 将水印信息隐藏到宿主子块中, 形成水印图像.在水印检测阶段, 利用水印嵌入过程中产生的安全密钥, 从水印图像中恢复密钥内容, 并将所提水印方案与已有的水印方法实施了对比测试, 试验数据显示了所提技术不仅具有更高的水印视觉隐秘性, 同样也具备较强的鲁棒性, 可以有效抵御多种不同的几何变换攻击类型.
由于所提水印方案采用了人工蜂群机制, 在一定程度上增加了算法的复杂度, 在未来研究中, 将对其进行优化, 在兼顾水印隐秘性与鲁棒性的同时, 也尽可能地降低算法耗时.







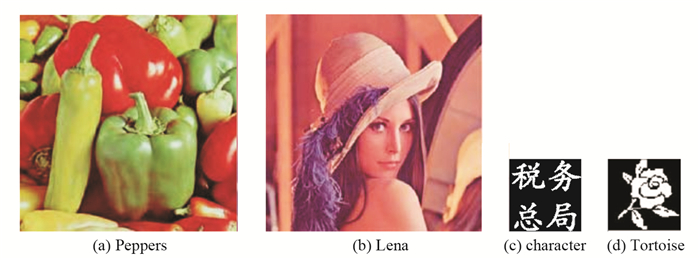


 DownLoad:
DownLoad: