-
在气候变暖背景下,全球各地极端降水过程呈总体增强态势,美国、英国、日本、澳大利亚、南非、印度等国的极端降水事件均呈显著上升或增多的趋势[1-6]. 近50年中国各地降水量虽没有明显的变化,但西南地区年降水量“西增东减”的分布形势却日益凸显,这与降水日数的增减关系密切[7]. 有研究[8]指出,西南4省(市)(川、渝、滇和黔)的极端降水强度在大部地区为增大趋势,而区域平均极端降水日数为下降趋势. 地处青藏高原和川西高原共同地形作用下的西南地区,天气尺度和中尺度系统的综合配置往往是引起区域内短时强降水过程的直接诱因[9-12],特别在西南涡影响下[13-14]极端降水事件时有发生,过程中强降水的密集区往往灾损重、社会民生影响大[15-16]. 为此迫切需要构建一种区域暴雨综合强度评估模型,既能满足气象灾害预警,以及气候监测业务对空间上局地极端强降水的高分辨需求,又能为重庆各级政府或公众媒体提供短时区域暴雨过程强度评估服务,具有十分重要的现实意义[17].
之前国内学者相关工作多是基于地面台站日降水资料展开的中国各地区域暴雨过程年际变率分析. 20世纪60年代以来,中国区域暴雨有10年的周期振荡,华南地区最为多发,长江中下游地区的暴雨综合强度呈微弱增强趋势,而四川盆地区域暴雨频次呈缓慢减少趋势[18-20]. 其中,区域暴雨过程的判识及综合指标的确立常需引入暴雨(或大雨)站次、极端日降水量、过程累积(或日平均)降水量、影响范围和持续时间等因子,极端阈值的筛选则常用广义极值分布(GEV)、百分位法和概率分布转换等方法[21-25]. 降水强度的精细化定量评估是气象现代化重要方向之一,而降水日数据可能高估(低估)长时弱降水(短时强降水)过程的强度,极端降水过程中采用小时尺度数据可留存更精确的细节信号[26]. 为统一小时—日尺度下降水过程强度表征因子的量纲,王莉萍等[27]将累计总雨量换算为平均日降水量,提取过程中的最大值,最大小时降水量也等效转换为日降水量;Zheng等[28]利用GEV法得到50 a中国大陆地区国家站五类极端滑动累积降水量升序排列的第70个和第90个百分位划分极端1-3级,1 h,3 h,6 h,12 h和24 h降水量达2级的阈值分别为75 mm,125 mm,160 mm,195 mm,230 mm;重庆站点1 h,3 h,6 h累积降水量阈值基本处全国极端1级范围内,12 h,24 h则在较强的极端2级;极端过程较强的地区主要在华南—东南沿海和华北东部—江淮地区[29]. 四川盆地短时降水率一般为18~36 mm/h,其极端值受地形影响较大[30]. Lu等[31]研究表明以幂函数表征极端降水事件的时长和面积范围是可行的,在此基础上本研究尝试以对数函数形式结合滑动小时累积雨量数据构建重庆单站及区域暴雨天气过程强度评估模型,通过历史个例回算,并借鉴气候监测业务中突显极端降水过程的单站影响及区域致灾效应,进一步落实气象防灾预灾减灾、保护人民生命财产安全的关键作用.
HTML
-
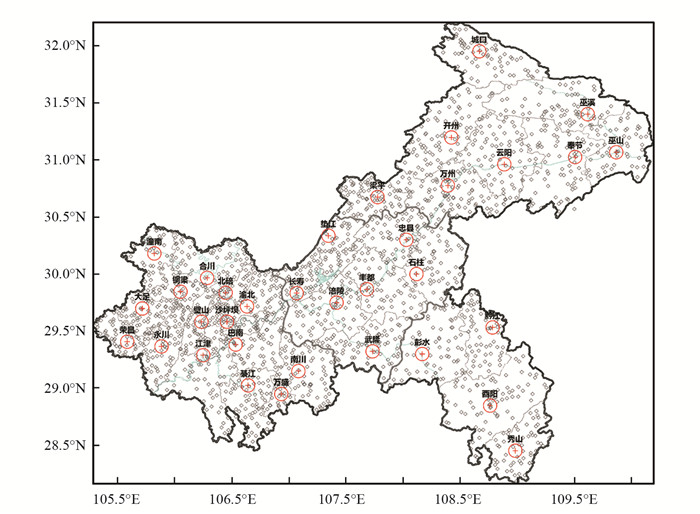
本研究主要利用重庆国家级气象观测站(简称国家站)和区域自动观测站(简称区域站)2类站点的5类滑动小时累积雨量数据进行研究(表 1),重庆区域范围内的两类站点总站数为2 092个,它们分布密集且均匀. 本研究将重庆的长寿、涪陵、丰都、垫江、武隆、石柱和忠县等7个行政区(县)定义为中部地区,该地区以东(西)为重庆东(西)部地区(图 1). 其中,区域站小时数据均源于国家气象信息中心的全国综合气象信息共享平台(CIMISS),并经过重庆市气象信息与技术保障中心质量控制,具体使用时我们对极端大值进行了再次复核.
-
单站暴雨过程强度评估模型见公式(1):
式中:I为单站暴雨过程强度,I>0表示该站出现单站暴雨过程,I值越大过程越强,反之亦然;T1(1 h),T3(3 h),T6(6 h),T12(12 h),T24(24 h)分别表示5类不同时长. 参考上海中心城区小时累积雨量达30~40 mm时开始出现暴雨积水、达50 mm时积涝会显著增多,北京城区道路出现积水的阈值则为40 mm/h[32-33],结合重庆近些年灾情较重的区域暴雨过程,综合考虑小时降水阈值既要突出降水序列中的极端个例,同时需保留强度近于极端的有效信号,本研究设定5类时长的滑动小时累积降水量阈值分别为R1=45 mm,R3=95 mm,R6=145 mm,R12=195 mm,R24=245 mm,其中,R1,R3和R24分别接近暴雨(24 h降雨50 mm)、大暴雨(24 h降雨100 mm)和特大暴雨(24 h降雨250 mm)量级[34],且R12,R24均对应我国极端2级阈值范围内,R1,R3,R6则均为1级[28]. Nn,Sn(n=1,3,6,12,24)分别表示5类时长各自达阈值的时次和总雨量,当Nn在任意一类时长的时次大于0时,利用公式(1)可得到该单站的暴雨过程强度. 重庆2016-2020年5年内50次区域暴雨过程中能达到Rn(n=1,3,6,12,24)各时长阈值的站数均值占总站数的比值分别为14.6‰,5.2‰,1.9‰,0.59‰,0.27‰. X0=1/2为时次权重(通过幂平均适当放大Nn值较大单站的雨强),1/1 000为避错因子,即在保证正常运算精度的前提下避免分母或真数为零的情况发生.
-
区域暴雨过程综合强度评估模型见公式(2):
式中:RI为区域暴雨过程综合强度,RI>0表示重庆出现区域暴雨过程,RI值越大区域过程越强,反之亦然. 具体算法为:对重庆区域内所有I>0的单站进行区间划分,由公式(1)得到单站1 h,3 h,6 h滑动小时数据同时达到阈值的最小过程强度为2.0,所以Z1和Z2分别设为I值在常区间(0,2)和强区间[2,2.8]的站数,RS1和RS2则对应Z1和Z2个站点的I值之和,X1=1/6和X2=1/3均为空间上的站数权重(突出强区间的幂结果),1/1 000为避错因子. 其中,n=1和n=2时对应的RI子项值分别称为常区间对数强度和强区间对数强度,当上述强区间和常区间对数强度中任意一个大于0时,便可利用公式(2)算出区域暴雨过程综合强度.
1.1. 重庆气象站点数据介绍
1.2. 重庆单站暴雨过程强度评估模型
1.3. 重庆区域暴雨过程综合强度评估模型
-
由公式(1)、公式(2)得到2016-2020年气象业务服务中所有区域暴雨过程的综合强度排位. 由表 2可知,区域综合强度序列与最大1 h,3 h,6 h雨强(即单站中能达到对应时长阈值的时次幂平均小时雨强的极大值)、极端均值序列的相关系数分别为0.76,0.80,0.68,0.77,且均通过99.9%的信度检验,由此可见,区域综合强度与极端雨强关系密切,特别是极端1 h、3 h幂平均小时雨强和极端均值都很突出. 综合考虑,通过某次区域过程中达到阈值的单站数及其较极端的强区间站数来表征重庆区域暴雨过程的影响范围和站点强度,由公式(2)推算:极端强区间站数为4站、常区间站数为36站时,区域综合强度可到0.9以上,因此,设定站数分类条件,即能(或不能)同时满足Z2≤4和1≤Z1+Z2≤40时,表 2中区域暴雨过程综合强度0.9可以等量划分为2类数据,前25位归为较强的极端密集类(Extreme Concentration,EC),后25位则为较弱的正常疏散类(Normal Dispersion,ND);空间分型如表 3所示,极端密集类可下分5型,即全域型(Regional Extreme Concentration,REC)、西部型(WEC)、东部型(EEC)、中西部型(MWEC)和中东部型(MEEC),由于正常疏散类的强度和致灾能力较EC类均偏弱,本研究在此不作分型且仅给出均值.
-
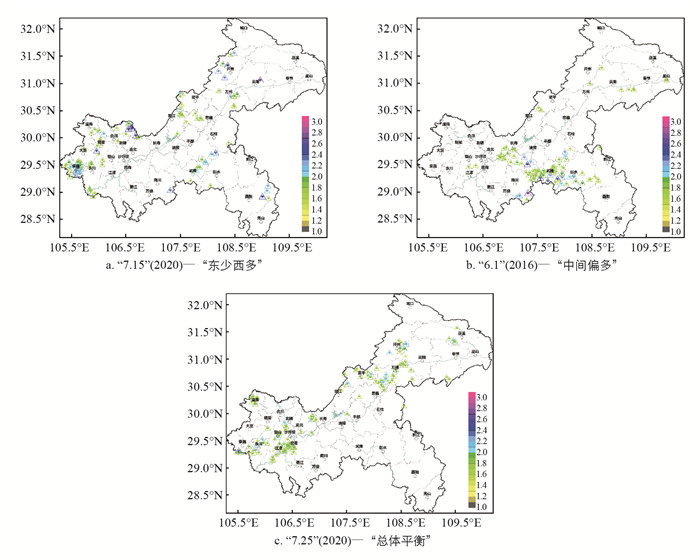
全域型在重庆极端密集类中占比为32%,区域综合强度均值达1.222,分型中排第三位,但单站数均值却为最多(表 3). 该型又可分“东少西多”“中间偏多”和“总体平衡”3种形态,归因可能是由中—大尺度天气系统如低涡或冷(暖)切变线等造成的. 其中,①“东少西多”形态:2020年“7.15”单站数和强区间站数的东—西对比值分别为25∶55和11∶19,荣昌和合川聚集的单站分别为最多和次多(图 2a);②“中间偏多”形态:2016年“6.1”密集影响中部的武隆、涪陵、丰都和长寿的48个站(强区间10个站),相比而言,在渝东的彭水—黔江和梁平—云阳—奉节—巫山共23个站(强区间3个站),渝西的中心城区、璧山和南川总计17个站(强区间3站)(图 2b),2017年“8.7”与之类似,主要密集影响重庆中部的垫江—长寿—丰都—石柱—忠县一线30个站(强区间5个站),而在渝西部和东部分别有12个站和17个站(图略),上述2例中东部与西部的站数之和都不及中部,可见中部地区在全域中的主体优势;③“总体平衡”形态:2020年“7.25”的单站数和强区间站数在中东部分别为53个站、7个站,西部分别为60个站、7个站(图 2c),2019年“7.31”、2017年“7.13”也很相似,二者单站数(强区间站数)在中东部和西部的比值依次为36(3)∶37(1)、18(2)∶15(3)(图略),全域站点分布基本平衡、极端强区间站数也很接近. REC三态平均强度由强到弱依次为“东少西多”(7.15,6.19,6.27)、“中间偏多”(6.1,8.7)、“总体平衡”(7.25,7.13,7.31)(表 3).
-
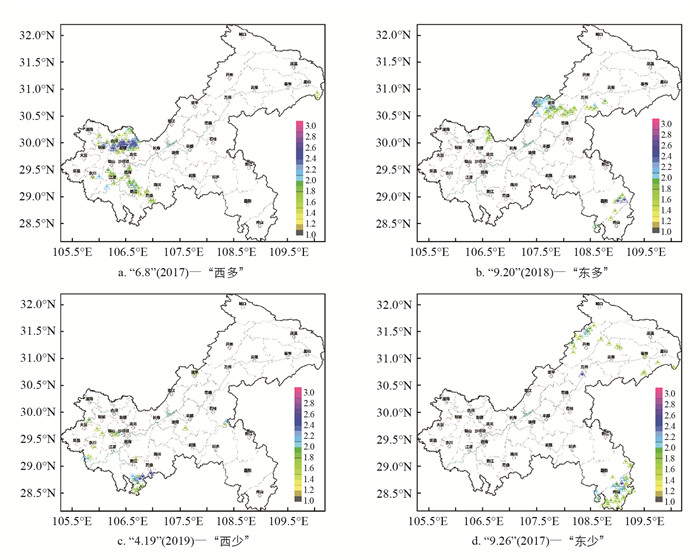
西部型和东部型在重庆极端密集类中占比分别为16%和20%,西部型的单站数和强区间站数均值较东部型分别偏多10.1个和5.8个,西部型、东部型的区域综合强度分别为最强和最弱,二者反差明显(表 3). 2017年“6.8”和2018年“9.20”分别为西部型和东部型的最强过程,前者79个站点集中于渝西的中心城区和合川、璧山、铜梁、永川、江津、綦江、万盛,占单站数的97.5%,含所有33个强区间站,合川保合最强,后者则主要分布在渝东的梁平—万州—云阳一线41个单站及酉阳7个站、秀山1个站,包含所有19个强区间站,最强站为酉阳米旺(图 3a-b). 对比而言,2019年“4.19”有23个单站(占比71.9%)聚集在渝西部的綦江、万盛、中心城区、永川,且含10个强区间站,万盛南门最强;2017年“9.26”有58个站、100%的单站在渝东部的秀山、酉阳、开州、万州、云阳、奉节和巫山,含所有14个强区间站,万州高峰最强(图 3c-d). 将上述两型逐一分析可见,WEC和EEC型均呈典型的片区式聚集,短时极端降水成灾的概率较大,西部型尤其值得重点关注.
-
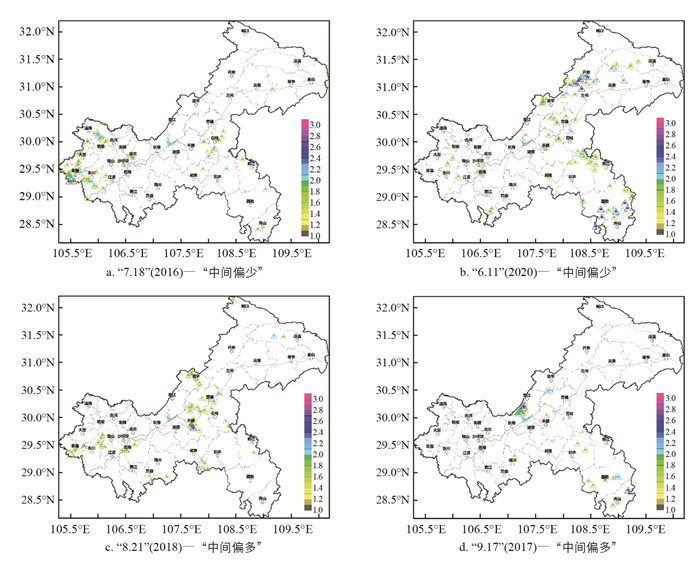
中西部型和中东部型在重庆极端密集类中占比分别为12%和20%,中东部型(排第2位)较中西部型(排第4位)总体偏强0.061,强区间站数均值也偏多3.6个(表 3). 上述两型以重庆中部为关键区,大体可划为以下2种形态,①“中间偏少”形态:2016年“7.18”主要影响渝西的中心城区—合川—潼南—大足—荣昌—永川一线的49个站(含10个强区间站),而在中部地区仅有石柱—丰都—武隆共计11个站(含2个强区间站),2020年“6.11”与之类似,中部的忠县、石柱和丰都也仅有15个站、含2个强区间站,而在东部的梁平—开州—万州—云阳—奉节—巫溪及彭水—黔江—酉阳—秀山累计有62个站、含24个强区间站(图 4a-b);②“中间偏多”形态:2018年“8.21”在中部的忠县—石柱—丰都—武隆沿线25个站含3个强区间站,而在渝西的荣昌—大足—永川—铜梁—璧山—中心城区一线有19个站且无强区间站,2017年“9.17”与之相似,中部长寿、垫江、忠县和丰都总计17个站,含7个强区间站,而在东部的酉阳、秀山、彭水和梁平总计11个站,含4个强区间站(图 4c-d). 综合MWEC和MEEC的两态强度对比得到,“中间偏少”(7.18,6.11,7.22,6.21,4.21,7.2)明显强于“中间偏多”(8.21,9.17).
-
2016-2020年重庆区域暴雨过程中正常疏散类区域过程综合强度、强区间对数强度分别较极端密集类偏弱0.666、0.513,单站数、强区间站数也分别偏少44.4次、11.7次(表 3),由此可见,疏散类相对密集类明显偏弱,但仍不能忽略局地极端强降水的影响,如表 2中2019年“8.6”过程属于ND类,这次过程中极端1 h,3 h,6 h,12 h幂平均小时雨强可达到110.8 mm/h,92.4 mm/h,71.4 mm/h和56.4 mm/h,其中,忠县洋渡镇单站强度达2.521,为ND类中最强单站,另外还有2016年“6.30”大足骑胜村(2.443)、2020年“3.27”彭水潘龙山(2.317)、2018年“4.4”丰都高镇(2.310)等(表略).
-
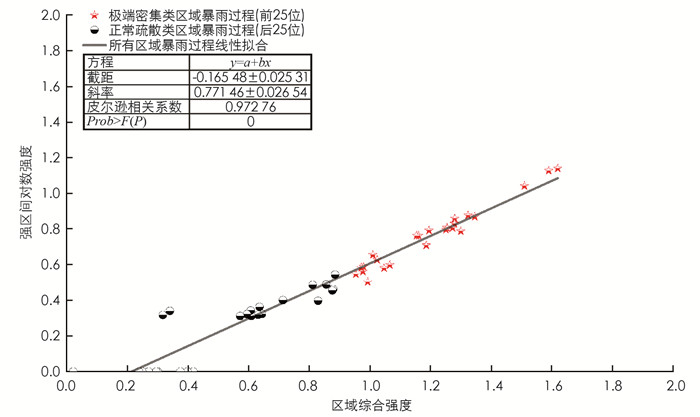
表 3中重庆极端密集类区域过程的综合强度序列与单站数、强区间站数的相关系数分别为0.71、0.97,且均呈显著性正相关(通过99.9%的信度检验). 图 5为5年间区域暴雨过程强区间对数强度和区域综合强度的线性回归,44个散点分布于趋势线附近,显著的正相关(皮尔逊系数=0.973和p=0)可通过99%的信度检验,这说明所有极端密集类区域暴雨过程和多数正常疏散类过程的区域综合强度均由[2,2.8]强区间站决定,强区间站的对数强度较常区间起更明显的主导作用,同时保留对无强区间站(即强区间对数强度为零,如ND类中的2016年“7.13”、2017年“5.2” “6.3”、2018年“4.12”、2019年“6.7” “5.18” “10.4” “10.7”和2020年“6.2”等9次过程)过程的评估能力,这与区域暴雨过程综合强度评估模型设计的初衷一致(表 2).
2.1. 2016-2020年重庆区域暴雨过程时空分析
2.1.1. 全域型(REC)
2.1.2. 西部型和东部型(WEC和EEC)
2.1.3. 中西部型和中东部型(MWEC和MEEC)
2.1.4. 正常疏散类(ND)
2.2. 2016-2020年重庆区域暴雨过程线性拟合
-
1) 本研究显示,重庆2016-2020年50场区域暴雨过程可分为两大类,在不考虑下垫面及城乡排水差异的前提下,应重点考虑极端密集类的致灾效应,但不能忽视正常疏散类的局地突发影响. 其中,极端密集类下分各型的平均区域综合强度由强至弱依次为WEC,MEEC,REC,MWEC,EEC,极端密集类的区域综合强度与单站数、强区间站数均呈显著正相关关系,后者相关系数达0.97.
2) 单站点分布范围相对较广的全域型可分为“东少西多”“中间偏多”“总体平衡”3态,而中西部型和中东部型极端密集类都分为“中间偏少”“中间偏多”两态,其中,REC和MWEC/MEEC下对应“东少西多”和“中间偏少”的致灾力为最强,相比而言,WEC/EEC体现为分片区聚集成灾,虽影响范围较小但短时极端强降水不可忽视,尤其是重庆西部地区,致灾概率较东部更大、破坏力也更强.
3) 对所有区域暴雨过程而言,区域综合强度与极端1 h,3 h,6 h幂平均小时雨强、极端均值的相关系数分别为0.76,0.80,0.68,0.77,区域综合强度与极端雨强关系密切;单站过程强度在[2,2.8]强区间的站点主导区域暴雨过程的综合强度,其对数强度与区域综合强度呈显著正相关,5年间88%的区域过程评估均可适用.
讨论:本研究发现,研究区域暴雨过程的强区间站与对应过程中大暴雨及以上量级的落区有较好匹配,常区间站则对应暴雨—大暴雨量级(图略). 需注意的是,公式(1)-(2)设计时,X0,X1,X23个幂指数之和恰为1.0,说明单站过程的时次和区域过程的站数各为1/2等权重. 单站暴雨过程评估模型中5类不同时长选取的阈值可根据研究或业务对常规或极端事件要求作相应调整,实际应用时建议根据各自需求用百分位数法来划定单站暴雨过程和区域暴雨过程的强度等级. 本研究主要针对极端降水过程的单站和区域强度进行评估,并未与实际灾情关联,且重庆范围内的区域站多位于城市楼房、公园、郊区或乡镇僻静地区,城市排水管网不一、下垫面情况复杂,因此,单站强度评估模型的应用对市郊、山地或道路两侧等高风险次生灾害区域具有指示意义.






 DownLoad:
DownLoad: