Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2022 Volume 47 Issue 10
Article Contents
Previous Article Next Article

JI Li, LIU Xiaoran, WU Qiang, et al. Establishment of Prediction Model of Early Flowering Period of Prunus Mume Based on PCA[J]. Journal of Southwest China Normal University(Natural Science Edition), 2022, 47(10): 59-66. doi: 10.13718/j.cnki.xsxb.2022.10.009
Citation: JI Li, LIU Xiaoran, WU Qiang, et al. Establishment of Prediction Model of Early Flowering Period of Prunus Mume Based on PCA[J]. Journal of Southwest China Normal University(Natural Science Edition), 2022, 47(10): 59-66. doi: 10.13718/j.cnki.xsxb.2022.10.009
shu

Establishment of Prediction Model of Early Flowering Period of Prunus Mume Based on PCA

  • 1.

    Weather Bureau in Beibei District of Chongqing City, Chongqing 400700, China

  • 2.

    Chongqing Institute of Meteorological Sciences, Chongqing 401147, China

More Information
  • Corresponding author: LIU Xiaoran ; 
  • Received Date: 06/06/2022
    Available Online: 20/10/2022

  • MSC: P49; S16

  • Taking the early blooming period of Chongqing Beibei Jingguan Suxin Chimonanthus as the research object, the variation characteristics of the early blooming period from 2007 to 2021 were statistically analyzed. Based on principal component analysis(PCA), a prediction model for the early blooming period from 2007 to 2021 was constructed by BP neural network algorithm and stepwise regression algorithm. The prediction effects of the two prediction models were compared and tested to select the best prediction model. The results show that the prediction fitting rate of the prediction model based on BP neural network algorithm in training is as high as 99%, and the correlation with the measured value is more than 0.9. In the back substitution test, the fitting rate was lower than that in training; the error between the prediction model based on stepwise regression algorithm and the measured value in training is greater than that based on BP neural network algorithm, with an average error of 1.7d. In the back substitution test, the effect is significantly better than what is based on BP neural network algorithm, and the linear correlation is also relatively stable. At the same time, the independent sample value, standard deviation and average absolute error of the prediction model based on stepwise regression algorithm are also better than the prediction model based on BP neural network algorithm. In general, the prediction model based on stepwise regression algorithm is better than the prediction model based on BP neural network algorithm.
  • 加载中
  • [1] 邵金彩, 杨灿芳, 关正, 等. 重庆市静观镇蜡梅产业现状与发展策略[J]. 北京林业大学学报, 2015, 37(S1): 29-33.

    Google Scholar

    [2] 杜军, 厉爱丽, 次旺顿珠, 等. 藏东南冬小麦生育期变化及其对气候变化的响应[J]. 生态学杂志, 2022, 41(4): 668-675.

    Google Scholar

    [3] 刘璐, 王景红, 傅玮东, 等. 中国北方主产地苹果始花期与气候要素的关系[J]. 中国农业气象, 2020, 41(1): 51-60. doi: 10.3969/j.issn.1000-6362.2020.01.006

    CrossRef Google Scholar

    [4] 李文静, 黄蔚薇, 李倩, 等. 长江流域油菜花期预报方法研究[J]. 中国农业资源与区划, 2020, 41(2): 101-108.

    Google Scholar

    [5] 林婷, 石雅, 王海洋, 等. 重庆地区毛叶木姜子种群结构及开花特征分析[J]. 西南师范大学学报(自然科学版), 2020, 45(7): 47-54. doi: 10.13718/j.cnki.xsxb.2020.07.007

    CrossRef Google Scholar

    [6] 王雷, 李玲莉, 王海洋, 等. 重庆市46种木本园林植物不同生长型对开花物候的效应[J]. 西南大学学报(自然科学版), 2020, 42(11): 86-94.

    Google Scholar

    [7] GONSAMO A, CHEN J M, WU C Y. Citizen Science: Linking the Recent Rapid Advances of Plant Flowering in Canada with Climate Variability[J]. Scientific Reports, 2013, 3: 2239. doi: 10.1038/srep02239

    CrossRef Google Scholar

    [8] 刘流, 甘一忠. 桃花迟早年型的冬季气候特点及花期预测[J]. 气象, 2006, 32(1): 113-116.

    Google Scholar

    [9] 张志薇, 高苹, 王宏斌, 等. 油菜花最佳观赏期变化及其对温度因子的响应[J]. 气象, 2019, 45(5): 667-675.

    Google Scholar

    [10] 孙明, 徐敏, 高苹, 等. 气象条件对悬铃木始花期的影响分析及预报模型构建——以江苏兴化为例[J]. 气象, 2021, 47(7): 862-871.

    Google Scholar

    [11] 岳高峰, 王丽萍, 刘丽, 等. 基于气象条件下的牡丹花期预报预测研究[J]. 江西农业学报, 2020, 32(2): 105-109.

    Google Scholar

    [12] 李菁博, 陈进勇, 程炜. 北京地区蜡梅冬季开花的影响因素研究[J]. 北京林业大学学报, 2012, 34(S1): 122-126.

    Google Scholar

    [13] 周贝宁, 毛恋, 花壮壮, 等. 碱性盐胁迫对夏蜡梅光合荧光特性影响[J]. 浙江农业学报, 2021, 33(8): 1416-1425.

    Google Scholar

    [14] 张家瑞, 杨姗. 重庆市北碚区蜡梅产业化开发利用思考[J]. 南方农业, 2014, 8(22): 58-60.

    Google Scholar

    [15] 赵冰, 张启翔. 中国蜡梅种质资源研究进展[J]. 西北林学院学报, 2007, 22(4): 57-61.

    Google Scholar

    [16] 程红梅, 周耘峰, 詹双侯. 蜡梅栽培现状及资源保护和利用[J]. 北京林业大学学报, 2007, 29(S1): 130-133.

    Google Scholar

    [17] 李海燕, 邵金彩, 王静, 等. NaCl胁迫对5年生蜡梅生长及生理特性的影响[J]. 东北林业大学学报, 2021, 49(3): 31-38.

    Google Scholar

    [18] 郭亚菲, 樊超, 闫洪涛. 基于主成分分析和粒子群优化神经网络的粮食产量预测[J]. 江苏农业科学, 2019, 47(19): 241-245.

    Google Scholar

    [19] 谭静, 陈正洪, 肖玫. 武汉大学樱花花期长度特征及预报方法[J]. 生态学报, 2021, 41(1): 38-47.

    Google Scholar

    [20] 朱兰娟, 金志凤, 张玉静, 等. 西湖龙井茶开采期影响因子及预报模型[J]. 中国农业气象, 2019, 40(3): 159-169.

    Google Scholar

    [21] 孙家清, 张志薇, 艾文文. BP神经网络在油菜花期预报中的应用[J]. 气象与环境科学, 2019, 42(4): 22-26.

    Google Scholar

    [22] 陈颖, 张仲伍. 基于聚类分析和主成分分析的城市空气质量评价——以山西省11个地级市为例[J]. 山西师范大学学报(自然科学版), 2020, 34(4): 72-78.

    Google Scholar

    [23] 李萍, 曾令可, 税安泽, 等. 基于MATLAB的BP神经网络预测系统的设计[J]. 计算机应用与软件, 2008, 25(4): 149-150, 184.

    Google Scholar

    [24] 徐敏, 赵艳霞, 张顾, 等. 基于机器学习算法的冬小麦始花期预报方法[J]. 农业工程学报, 2021, 37(11): 162-171.

    Google Scholar

    [25] 冯敏玉, 孔萍, 胡萍, 等. 基于花前物候利用灰色关联分析法建立油菜花期预报模型[J]. 中国农业气象, 2021, 42(11): 929-938.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(5)  /  Tables(4)

Export Citation
PDF
XML

Article Metrics

Article views(1380) PDF downloads(263) Cited by(0)

Access History

Other Articles By Authors

Establishment of Prediction Model of Early Flowering Period of Prunus Mume Based on PCA

    Corresponding author: LIU Xiaoran ; 
  • Received Date: 06/06/2022
  • Available Online: 20/10/2022

Abstract: Taking the early blooming period of Chongqing Beibei Jingguan Suxin Chimonanthus as the research object, the variation characteristics of the early blooming period from 2007 to 2021 were statistically analyzed. Based on principal component analysis(PCA), a prediction model for the early blooming period from 2007 to 2021 was constructed by BP neural network algorithm and stepwise regression algorithm. The prediction effects of the two prediction models were compared and tested to select the best prediction model. The results show that the prediction fitting rate of the prediction model based on BP neural network algorithm in training is as high as 99%, and the correlation with the measured value is more than 0.9. In the back substitution test, the fitting rate was lower than that in training; the error between the prediction model based on stepwise regression algorithm and the measured value in training is greater than that based on BP neural network algorithm, with an average error of 1.7d. In the back substitution test, the effect is significantly better than what is based on BP neural network algorithm, and the linear correlation is also relatively stable. At the same time, the independent sample value, standard deviation and average absolute error of the prediction model based on stepwise regression algorithm are also better than the prediction model based on BP neural network algorithm. In general, the prediction model based on stepwise regression algorithm is better than the prediction model based on BP neural network algorithm.

    HTML

  • 蜡梅为蜡梅科蜡梅属植物，是珍贵的天然香料植物[1]. 重庆市北碚区蜡梅种植面积占全市蜡梅总面积的85%，有500多年种植历史，与河南鄢陵、湖北保康并称为“中国三大蜡梅基地”，每年吸引了大量的游客来此地观赏蜡梅. 科学、准确地开展蜡梅花期预报可指导人们合理安排时间观赏蜡梅，促进当地生态旅游发展.

    关于植物花期与气候变化规律，以及花期预测技术国内外均有大量的研究[2-6]. Gonsamo等[7]模拟加拿大19种植物的始花期变化；刘流等[8]对桂林桃花开花期与气象要素的关系进行研究，发现桃花开花期与当年1月下旬到2月下旬气温和上年冬季降水量有显著的相关性；张志薇等[9]基于1986-2016年油菜花物候观测资料，分析了盛花期的物候特征及与温度因子的关系；孙明等[10]基于1990-2020年悬铃木花的物候资料，明确了关键气象因子对始花期的定量影响，并建立预测模型；岳高峰等[11]以牡丹花花期为预报主体，选取气温、积温、日照和空气湿度气象因子进行主成分分析和逐步回归分析，建立多元回归预测模型，为牡丹文化节组委会提供决策依据. 相对而言，由于蜡梅种植面积少，种植范围不广，对蜡梅花期研究较少，目前国内外关于蜡梅的研究报道主要集中在栽培技术[12-17]、化学成分、品种等方面.

    近年来，机器学习作为人工智能领域的重要分支，国内外越来越多的学者将机器学习技术应用于各个领域，其中在作物预测方面的研究取得了较好的成绩[18-20]. 这些分析方法能够从多水平、多因素着手，综合分析各指标的整体效应，使筛选出的结果更具科学性. 本研究以重庆市北碚区静观素心蜡梅早熟品种的初花期为研究对象，统计分析2007-2021年初花期变化特征，基于PCA主成分分析法，通过BP神经网络算法及逐步回归算法，对蜡梅初花期预测进行预测试验，以期为科学有效开展蜡梅初花期气象服务提供理论依据和技术支持.

1.   资料与方法

    1.1.   资料

    1.1.1.   资料来源

  • 素心蜡梅初花期是指蜡梅树枝开花率为20%左右的时间，素心蜡梅早熟品种初花期2007-2013年资料为课题组对北碚区静观镇、柳荫镇等地实地走访调查所得，2014-2021年数据来源于静观蜡梅气象服务站观测数据. 气象资料是北碚区国家气象观测站2007-2021年逐日资料，包括平均气温、最低气温、最高气温、降水量、日照时数等，气温、降水量、日照时数的日气象资料统计为旬资料，雨日数为日降水量L≥0.1 mm的日数.

    蜡梅初花期转换为年日序值，即1月1日为1，1月2日为2，以此类推.

    • 1.1.2.   气象因子

  • 影响蜡梅花开花的过程主要是受气温、降水、日照的影响. 光、温、水条件的匹配程度影响初花期的早晚时间，因此为筛选出对蜡梅花初花期有影响的气象因子，本研究将气温、降水、日照作为预测初花期的初选因子. 蜡梅一般在10月进入长枝期，11月进入定型期，花芽逐渐生出，早熟初花期一般在12月11日左右，因此本研究主要选取11月的18类气象因子(表 1).

    • 1.2.   研究方法

    1.2.1.   PCA

  • 主成分分析(PCA)[21-22]是通过对协方差矩阵进行特征分析，在减少数据维数的同时，保持数据集对方差贡献最大的目的. 利用数据降维的思想，在损失较少数据信息的前提下，把多个指标转化成几个为数较少的综合指标的多元分析方法，各个主成分是原始变量的线性组合，彼此之间互不相关. 主成分分析以方差作为信息量的测度，取累计贡献率大的几个成分作为主成分.

    • 1.2.2.   BP神经网络预报方法

  • BP神经网络算法是目前应用最广泛的预测方法，其基本思想是工作信号正向传递和误差信号反向传递两个子过程，学习规则和目标是使用最速下降法，通过反向传播不断调整网络的权值和阈值使全局误差系数最小，学习本质是对连接权值的动态调整. 基本结构由输入层、隐层和输出层构成[23].

    • 1.2.3.   逐步回归预报方法

  • 采用回归方法是根据自变量的取值来预测因变量的取值[24-25]，以变量对目标的影响程度大小，从大到小逐个引入回归方程，再对回归方程所含的变量进行检验，显著则引入方程，不显著则剔除，直到没有显著因素可以引入，或不显著变量需剔除为止. 本文主要选取主成分作为初花期预测因子，采用SPSS软件，利用“步进法”建立蜡梅花初花期预测模型.

    • 1.2.4.   数据评估方法

  • 偏度系数是统计数据分布偏斜方向和程度的度量，用于衡量数据的对称性的特征数；峰度系数是表征概率密度分布曲线在平均值处峰值高低的特征数. 本研究主要采用SPSS软件对蜡梅花序日进行正态分布性检验[23].

    • 1.2.5.   数据预处理

  • 通常使用的机器学习算法将数据样本分为训练集与测试集，通过训练集数据建立模型，测试数据则用于检验模型的泛化能力，因此在确定建立模型前，为消除指标之间的量纲影响，需对数据进行归一化处理. 通过对数据进行分段建模的方式拟合，本研究以2007-2017年有效初花期数据作为训练集数据，再选取高影响气象因子，以初花期日序为输入目标，利用SPPS Modeler软件构建BP神经网络预测模型和逐步回归预测模型，然后利用boosting集成学习思想，为每一个训练样本赋一个权重，在每一轮提升过程结束时自动调整权重，提高预测模型的泛化能力，防止模型过度拟合. 最后为进一步验证该模型的准确性，对2018-2021的数据进行预测效果检验.

2.   结果分析

    2.1.   蜡梅初花期及气象要素分析

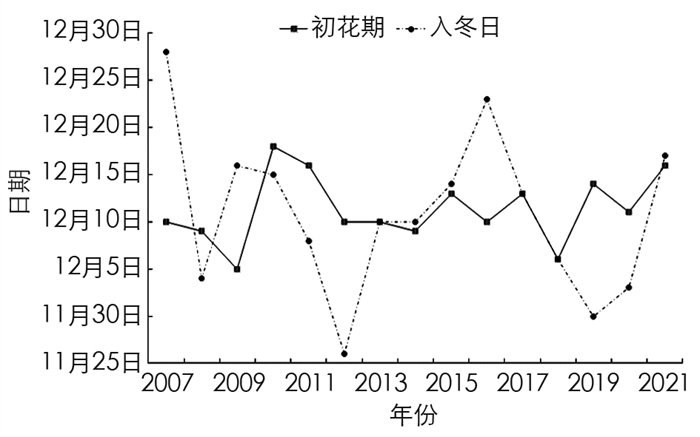
  • 由图 1蜡梅花初花期可知，2007-2021年，蜡梅初花期主要集中在12月，平均初花期在12月11日左右，接近入冬初日. 其中年份较晚的初花期出现在12月18日(2010年)，最早的初花期出现在12月5日(2009年)，最早和最晚的日期相差13 d. 采用偏度和峰度检验法，对蜡梅花序日进行正态分布性检验[23]，计算出花序日时间序列的偏度、偏度标准差、峰度、峰度标准差，其值分别为-0.134，0.580，-0.055，1.121，发现偏度和峰度均在±1.96之间，说明静观蜡梅初花期资料符合正态分布的特征，可以通过建立回归模型进行预报.

    根据气象学定义，入冬日为当年滑动平均气温序列连续5天小于10 ℃，则以其对应的常年气温序列中第一个小于10 ℃的日期作为入冬初日，由图 1可见入冬日在2007年后略有提前，2007-2021年蜡梅初花期多数晚于入冬初期，相差不超过5 d，其中入冬初日最早出现日期为2019年11月30日，蜡梅初花期则为12月14日，入冬初日最晚出现日期为2007年12月28日，但是当年蜡梅初花期并未延后，接近平均初花期.

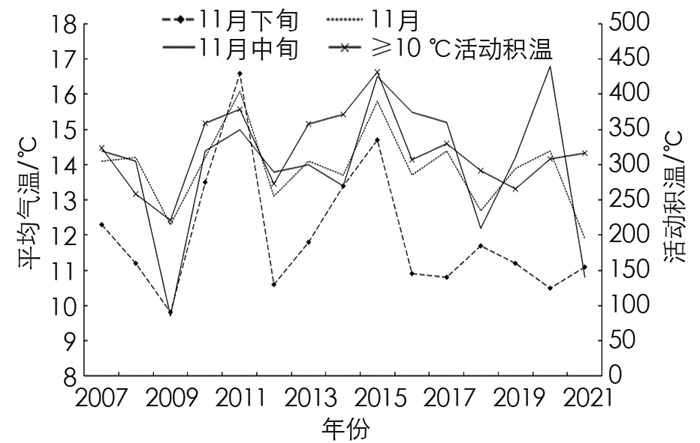
    对2007-2021年蜡梅花开花前期气温趋势图(图 2)分析发现，近16 a的时间段内，11月平均气温为13.9 ℃，11月中旬平均气温为14.0 ℃，11月下旬平均气温为12.0 ℃，其中下旬气温除2009年为9.8 ℃，2011年为16.6 ℃外，气温主要集中在10 ℃~14 ℃之间，其中花日序与11月下旬平均气温相关系数最高(0.444)，这与前人研究结论基本一致[24]，即蜡梅开花时的适宜温度在10 ℃左右，温度越低，花蕾比例越高，且随着温度的升高，花蕾开花数量随之增加. 由图 2可知，t≥10 ℃活动积温趋势与11月中旬平均气温趋势基本一致，t≥10 ℃活动积温主要集中在221 ℃~432 ℃之间，其中2015年积温最大，为431.2 ℃，其次是2011年，为379.1 ℃，最小值出现在2009年. 花日序与t≥10 ℃活动积温呈正相关性，相关系数为0.486，说明花期与t≥10 ℃活动积温的关系较为密切.

    • 2.2.   蜡梅花初花期气象因子筛选

  • 本研究利用SPSS软件将表 1中的18个气象因子作为原始输入变量，以降维方式提取主成分，提取出的主成分是原始变量的综合考量，简化数据的复杂度. 采用PCA算法分别对18项影响因素进行特征值和特征向量计算，从表 2中可知，前6个主成分均大于1，累积贡献率为85.239%，对比旋转载荷平方和的结果，发现两者累计贡献率一致，基本上可以反映气象因子的大部分信息.

    表 3是2007-2021年气象因子主成分特征向量值，由表 3可知，在第1主成分的特征向量中，特征值大于0.8的因子是t≥10℃活动积温、11月中旬极端最低气温、11月中旬平均气温，说明第1主成分中初花期与11月中旬的气温有着紧密的相关性；在第2主成分的特征向量中，特征值绝对值大于0.8的因子是11月上旬日照、11月上旬极端最高气温、11月雨日，其中正值最大的是11月上旬日照(0.862)，负值最小的是11月雨日(-0.862)，说明第2主成分中初花期与光照和雨水关系较大；第3主成分的特征向量中，最大的正值是11月中旬日照，而最小的负值是11月下旬日照，说明在第3主成分中初花期主要受日照的影响；同理，第4主成分中初花期受11月上旬气温的影响较大，第5主成分中初花期受11月上旬降水和11月下旬最高气温的影响较大，第6主成分中初花期受11月中旬降水的影响较大. 根据主成分的特征向量，获得6个主成分与气象因子间的线性方程，即第1主成分(F1)为各气象因子与主成分系数的积相加的总和：

    • 2.3.   预测模型结果分析

    2.3.1.   模型构建

  • 以主成分分析法得到的影响蜡梅花初花期的6个主成分作为预测模型的影响因子，以蜡梅花初花期年日序为目标，构建BP网络神经预测模型，在建立BP神经网络预测模型过程中，基于Boosting集成学习思想，模型的拟合高达99%，其中预测值与实际值的相关性为0.99，通过了α=0.01的检验，标准差为0.171，均方根误差为0.17.

    以6个主成分作为自变量，蜡梅花初花期日序为因变量，利用SPSS软件，运用逐步回归算法建模，得到预报模型：

    从模型中可看出，主成分2是影响蜡梅花初花期的关键气象因子，结合表 3可知，11月上旬的光照、气温及雨水日数是影响初花期主要气象因子. 利用逐步回归预报模型对2007-2017年的初花期日序进行拟合，模型预测值与实际值的相关性为0.77，通过了α=0.01的检验，标准差为2.212，均方根误差为2.10.

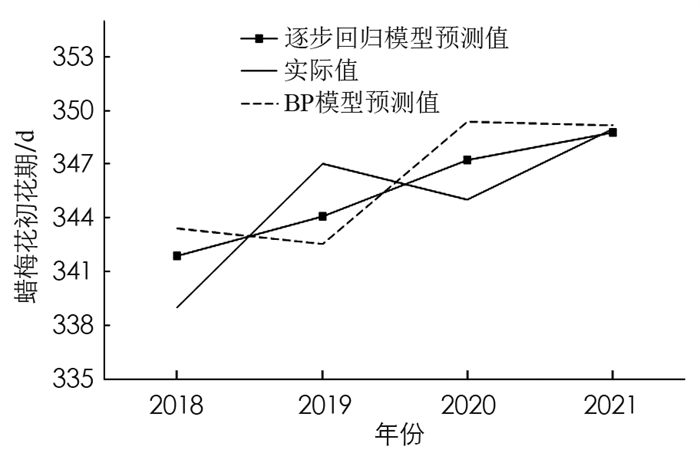
    绘制模型预测值与实际值对比发现(图 3)，BP模型预测值与实际值的趋势，除2008年外，其余年份的趋势基本重合，其中误差最大年份是2008年，误差为1 d；基于逐步回归算法的预测值与实测值的误差较BP神经网络的模型较大，平均误差有1.7 d，最小误差出现在2011年，与实测值基本一致；最大误差出现在2010年(5 d)，其余年份与实测值基本相差1 d左右.

    • 2.3.2.   预测模型回代检验

  • 将2018-2021的数据代入该模型进行进一步预测效果检验，绘制检验结果对比图(图 4)，从图中可知，基于逐步回归算法的预测模型较基于BP神经网络算法的预测模型的误差较小. 基于BP神经网络算法的预测模型回代检验平均误差为3.3 d，其中2019年预测值与实测值误差最大(提前了5 d)，误差值最小值出现2021年，与实测值基本一致，2018年和2020年均延后了4 d；基于逐步回归算法的预测模型的平均误差为2.1 d，误差值最大的年份同样出现在2019年，延后了3 d，误差值最小的年份出现在2021年，与实测值基本一致. 造成误差的原因是由于构建预报模型时出于预报时效性考虑，选择11月的气象要素作为主要因子，若蜡梅受前期气象要素的影响，导致生长期的变化，花期也易相应得到改变；同时若临近预测期的天气情况有较大的关系，若常年初花期前出现持续晴好天气或者阴雨天气，易提前或推迟花期. 因此在实际应用过程中，需根据蜡梅生育期情况，结合实际气候趋势，进行订正.

    • 2.4.   评价

  • 对比2种建模方法发现(表 4)，在2007-2017年训练集中，2种预测模型的效果都较好，其中基于BP神经网络算法的预测模型效果最好，其预测值的独立样本更接近实测值，标准差低于基于逐步回归算法的预测，线性相关性也较强.

    选取2018-2021年的有效数据作为检验样本，由表 4中可知，2种预测模型的预测效果较训练时有所下降，从检验样本来看，基于逐步回归算法的预测模型独立样本值，即最大值、最小值都较基于BP神经网络算法的预测值更接近实测值；从标准差和平均绝对误差来看，同样基于逐步回归算法的预测模型表现要优于另外一种预测模型. 同时从线性相关性来看，基于逐步回归算法的预测模型在建模和回代检验的过程中，线性相关性都较稳定，均在0.78左右. 总体来说，从预报检验结果来看，基于逐步回归算法的预测模型在检验过程中更优于基于BP神经网络算法的预测模型.

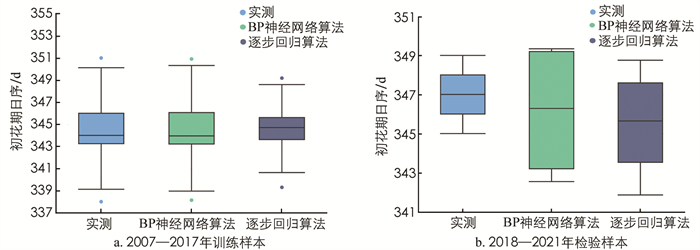
    绘制2007-2017年模型预报初花期日序箱线图(图 5a)，从箱线上下边缘可见，基于BP神经网络算法的预测模型较基于逐步回归算法的模型更接近实测值；从箱体来看基于逐步回归算法的模型的预测值较为集中，箱体主要在343.3~345.6之间，中位数344；基于BP神经网络算法的模型的箱体则在343.2~346.1之间，中位数343；实测值的箱体则在343.25~346之间，中位数344. 综上所述，基于BP神经网络算法的模型较接近实测值.

    绘制2018-2021年模型预报初花期日序箱线图(图 5b)，从图中可知，2018-2021年实测值整体较为集中，上边缘349，下边缘345，上四分位348，下四分位346，中位数347；基于BP神经网络算法的预测值的上边缘和上四分位基本接近，分别是349.34和349.19，下边缘342.54，下四分位343.19，中位数346.28；基于逐步回归算法的模型的上边缘348，下边缘341.85，上四分位347.59，下四分位343.52，中位数345.6；两个模型对比可见，基于逐步回归算法的预报模型较基于BP神经网络算法的模型的最大值与实测值基本一致，最小值基于BP神经网络算法更接近实测值，但从整个箱体来看，基于逐步回归算法的模型较BP神经网络算法更稳定.

3.   结论与讨论

  • 为探索蜡梅花早熟品种的初花期的预测，本研究基于PCA通过BP神经网络算法及逐步回归算法，构建了2007-2021年初花期预测模型，并对2种预测模型的预报效果进行对比检验，筛选最优预测模型. 结果表明，基于BP神经网络算法的预测模型在训练中的预报拟合率高达99%，与实测值的相关性超过了0.9，拟合度较高，在回代检验中拟合率低于训练时；基于逐步回归算法的预测模型在训练中与实测值误差大于基于BP神经网络算法，平均误差为1.7 d，在回代检验中效果明显优于基于BP神经网络算法，且线性相关性也较稳定；同时在回代模型中基于逐步回归算法的预测模型的独立样本值、标准差和平均绝对误差也同样优于基于BP神经网络算法的预测模型. 总体来说，基于逐步回归算法的预测模型更优于基于BP神经网络算法的预测模型.

    花期预测模型的基础就是预报因子的筛选，主成分分析法(PCA)是机器学习方法中对多指标综合分析方法，这种分析方法能够从多水平、多因素着手，综合分析各指标的整体效应，使筛选出的结果更具有科学性. 但是蜡梅花开花的生育期，不仅仅受气象要素的影响，还与田间管理、肥料、品种等多方面有着密切的关联，因此通过机器学习建立预测模型，还存在一定的偏差. 同时，本研究蜡梅花的生育期观测资料还较少，预测模型还有较大的不确定性，因此在后续研究中，需进行持续观测，收集更多的蜡梅花花期样本资料，不断地调试模型，提高预测精度.

Figure (5)  Table (4) Reference (25)

Catalog

    Copyright Journal of Southwest China Normal University(Natural Science Edition)

    Address： Tel：023-68252540，68254576，68254478 E-mail：xbbjb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return