本研究利用沈阳市2007-2011年6、7、8月探空因子与闪电定位资料.探空数据来自沈阳站(54342)，一日2次，分别是北京时间8：00点和20：00点，将每次探空得到的因子与探空后12 h内闪电定位系统探测到的雷暴发生与否组成样本对，经统计样本数量为910个样本.这里定义：若探空后12 h内，沈阳站附近50 km范围内发生一次及以上的雷暴即认为该样本是雷暴样本，否则为非雷暴样本.

多个因子中有些与雷暴发生与否相关性不大，应予以甄选.由于对流参数物理量是连续型因子，雷暴发生与否为0，1变量，所以不可直接求出其相关系数，而是求出其双点序列相关系数^[16].

78个因子双点序列相关系数(r)大于或等于0.25的有12个，序列号分别是1，2，3，4，7，9，13，17，18，57，72，73，如表 1所示.其中序列号57因为样本缺失过多，只有95个可用，所以不予考虑. 1，2号因子分别是总指数T和修正总指数mTT，3，4号因子分别是K指数和修正K指数，为了避免信息重复，所以保留相关系数略大的修正总指数和修正K指数.因此，参与预报的因子共计9个，分别是：修正总指数、修正K指数、沙氏指数、条件稳定度指数、条件对流稳定度指数、Teffer指数、Charba总指数、瑞士雷暴指数、抬升指数这9个因子，样本168、645号有缺失，至此，共有样本908个，其中雷暴样本402个，非雷暴样本506个.

908个样本中，3/4的样本用来训练网络，1/4的样本用于检验.为避免样本之间的相关性影响预报结果，故这里采取随机选取的方式来进行样本划分.因此样本被分为681个训练样本和227个独立检验样本. 908个样本中，雷暴样本有402个，占44.27%；681个训练样本中，雷暴样本有305个，占44.79%；227个独立检验样本中，雷暴样本有97个，占42.73%.网络输出采用两级分类，将有雷暴样本设计成[0.9，0.1]，无雷暴样本设计成[0.1，0.9]，并将训练样本对进行归一化，数值范围归一到[0.1，0.9]，独立检验样本按照与训练样本同样的方法进行归一化处理.

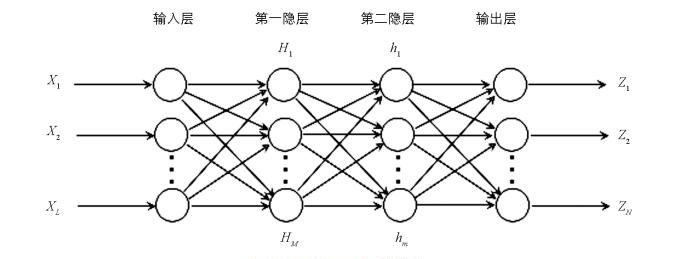
BP人工神经网络可有效地用于复杂的非线性函数的逼近，一个3层的前馈网络能够实现任意精度的连续函数映射^[18]，两个隐层的神经网络则可以解决各种分类问题^[19].因此本文尝试构建两个隐藏层的BP网络，下文称为双隐形BP网络，双隐层BP网络模型示意图如图 1所示.

训练样本集是影响BP网络性能优劣的关键，神经网络是以样本在事件中的统计几率来进行训练和预测的.归一化是归纳统一样本的统计分布性，可以简化计算，缩小量值，加快网络的收敛.归一化在[0,1]之间是统计的概率分布，归一化在[-1，+1]之间是统计的坐标分布.兼顾sigmod函数的定义，这里采取式(1) 对输入输出样本进行[0.1，0.9]之间的归一化.

这里，P表示归一化前的输入数据；P_min表示矩阵P的最小值；P_max表示矩阵P的最大值；X表示归一化之后的输入矩阵.

选择算法对网络进行训练时，在网络参数很多，需要考虑存储容量问题时，选择共轭梯度法.经试验，这里选择Scaled共轭梯度法trainscg.

各层神经元的传递函数根据需要，不同层内采取不同的传递函数组合，并且一般常采用S形函数和线性函数组合，S形函数能将跨度很大的数值压缩到一个很小的固定范围内.输出层常采用线性函数，这样整个网络的输出可以取实数域内任何值.双隐层的网络结构，需要3层传递函数，选取tansig和purelin的结合，在试验中，最终确定tansig-tansig-purelin组合. tansig的表达式如下：

其中，P表示输入矩阵，W表示权值矩阵，b表示偏置矩阵，A表示输出.

怎样寻求泛化能力最大的网络是网络构建的一个难题，网络的泛化性能是指神经网络对训练样本以外的新样本的适应能力.在网络的训练过程中经常会出现过拟合现象，即在网络训练过程中，从某一次训练开始，随着网络的训练能力提高，仿真的能力反而下降，解决这个问题的一种办法是：在数据输入中，给训练的数据分类，分为正常训练数据、变量数据、测试数据，3种数据占用全部样本的70%，15%，15%.设定参数maxfail为6(最大失败次数)，在网络训练的过程中，如果从某一步开始，变量数据的误差不降反升，则Validation Checks开始计数，当计数到6，则认为网络陷入过拟合，停止训练.

目前隐节点的选取还没有一个统一的标准，前人也进行了许多研究，得到几种隐节点的计算公式^[19-22]，由于这些公式只是大致给出了隐节点的取值范围，而不同的研究问题之间有很大的差别，所以仅根据上述公式来确定隐节点数不合适，这里将其作为参考，尝试多种隐节点数组合，根据网络训练的MSE，最终确定隐节点数.

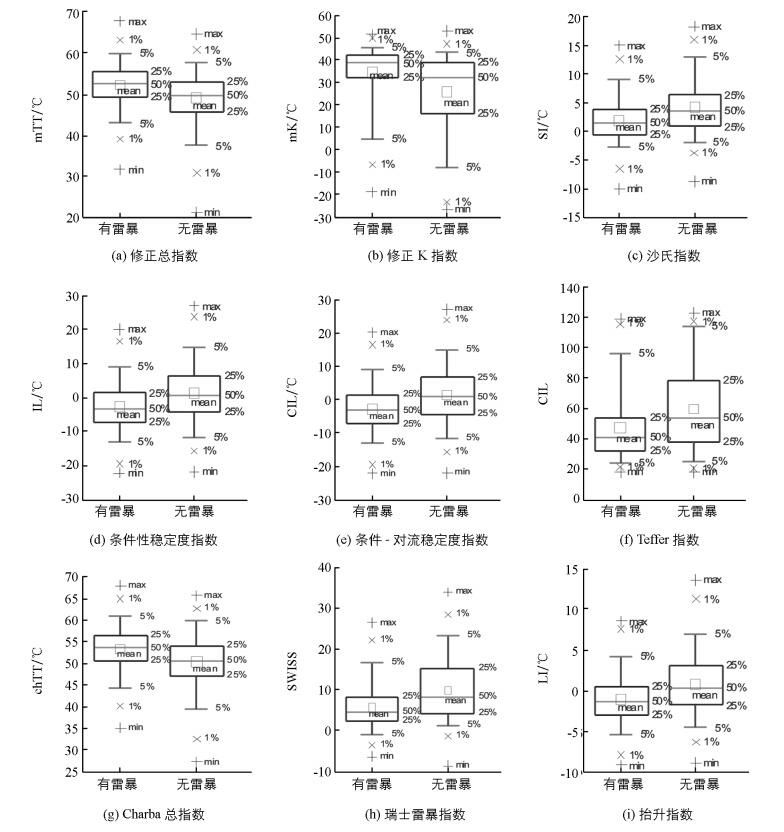
将选取的9个探空因子分别统计雷暴样本、非雷暴样本的数值分布，制成方框-端须图，纵坐标为因子数值.一般来说，对于大量的统计测量数据，均可视作是呈现正态分布，在此将这9个因子视为呈现正态分布.

如图 2所示，在每个长方形上下底分别表示正态分布两端占该类样本总数(有雷暴样本或无雷暴样本)25%个例的因子数值，方框内的横线表示占该类样本总数50%个例的因子数值，从长方形上下边延伸出的线段端点表示占该类样本5%个例的因子数值，“×”表示的是占该类样本总数1%个例的因子数值，最上端和最下端的“+”表示该类样本的最大和最小值，方框中的‘□’表示该类样本均值.

1) 修正总指数

图 2(a)给出了修正总指数的分布，可以看出雷暴样本的数值偏大，雷暴样本的中位数是52.4 ℃，说明雷暴样本有半数＞52.4 ℃，而在这一区间仅有约25%的非雷暴样本修正总指数的定义为

下标500表示气压，T与T_d分别表示地面至850 hPa的平均温度与平均露点温度.由定义可以看出mTT越大，越容易发生对流天气.

2) 修正K指数

图 2(b)给出了修正K指数的分布，可以看出雷暴样本数值偏大，中位数接近40 ℃，非雷暴样本的中位数位于30 ℃左右. 79.35%的雷暴样本mK大于30 ℃，59.95%的雷暴样本mK大于40 ℃，相应的非雷暴样本对应的比例为54.35%，41.90%. mK的定义中考虑了温度之间率、底层水汽条件、中层饱和度以及地面温度状况，因此K指数可以反映大气的层结稳定情况，mK值越大表示气团低层越暖湿，稳定度越小，层结越不稳定，因而越有利于对流产生.

3) 沙氏指数SI

图 2(c)给出了沙氏指数的分布，可以看出雷暴样本的沙氏指数偏低，71.89%雷暴样本的SI小于3 ℃，而非雷暴样本在这一区间的比例有45.65%.在SI小于0 ℃区间，雷暴样本比例达到32.84%，非雷暴样本仅有15.81%.沙氏指数作为一个能够表征大气稳定状况的指数，它定义：850 hPa等压面上的湿空气团沿干绝热线上升，到达凝结高度后再沿湿绝热线上升至500 hPa时所具有的气团温度T_s850与500 hPa等压面上的环境温度T₅₀₀的差值.当SI小于0时，大气层结不稳定，且不稳定程度与负值成正比.反之，当SI大于0时，表示气层是稳定的. SI虽然也是表示条件性稳定度的，但只有当起始高度为850 hPa，上层为500 hPa时，它才与IL类似.

4) 条件性稳定度指数

当IL小于0，为条件性不稳定；IL为0，为中性；IL大于0，为条件性稳定. 图 2(d)可以清晰地看出雷暴样本的中位数位于0以下，而非雷暴样本的中位数位于0之上，67.66%的雷暴样本处于不稳定状态，仅46.44%的非雷暴样本处于这一区间.

5) 条件对流稳定度指数

条件性稳定度指数考虑的是一小块空气上升得到的，而对流性稳定度考虑的是整层空气抬升得到的，常把IL与IC相加称为条件-对流稳定度指数，也有称为位势稳定度指数，因此当CIL小于0，为对流性不稳定；CIL为0，为中性；CIL大于0，为对流性稳定.由图 2(e)可以看出近70%的雷暴样本处于不稳定状态下.

6) Teffer指数

图 2(f)给出了Teffer指数的分布，可以看出雷暴样本该指数数值偏小，雷暴样本有75%位于53.59以下，而位于此区间的非雷暴样本仅有50%.

7) Charba总指数

由图 2(g)可以看出，雷暴样本的值较大，雷暴样本有50%位于54 ℃以上，而这个区间非雷暴样本仅有25%，该指数用于表征对流稳定度，数值越大，越不稳定，越容易发生强对流天气.

8) 瑞士雷暴指数

瑞士雷暴指数用于确定是否有雷暴发生，它类似强天气威胁指数，这是一个无量纲的指数，一般来讲，当SWISS小于5.1时预报有雷暴. 图 2(h)给出了瑞士雷暴指数的分布，54.73%的雷暴样本该指数小于5.1，而非雷暴样本只有29.64%小于5.1.

9) 抬升指数LI

图 2(i)给出了抬升指数的分布，可以看出雷暴样本的沙氏指数偏低，67.66%雷暴样本的LI小于0 ℃，而非雷暴样本在这一区间的比例有46.44%；雷暴样本的均值及中位数均在0 ℃以下，而非雷暴样本均在0 ℃以上.抬升指数表征的是气块从低层900 m高度沿干绝热线上升，到达凝结高度后，再沿湿绝热线上升至500 hPa时所具有的温度T_s与500 hPa等压面上的环境温度T₅₀₀的差值.当LI小于0时，且不稳定程度与负值成正比.反之，当LI大于0时，表示气层是稳定的.

总的来说，这9个因子表征着大气层结稳定度、对流稳定度、底层水汽等条件，而这些条件与对流的产生、发展有紧密的联系，因此一定程度上包含了雷暴的信息，并且这些因子与辽宁地区雷暴发生与否相关性较高，因此利用这9个因子作为辽宁地区雷暴潜势预报的因子是可行的.

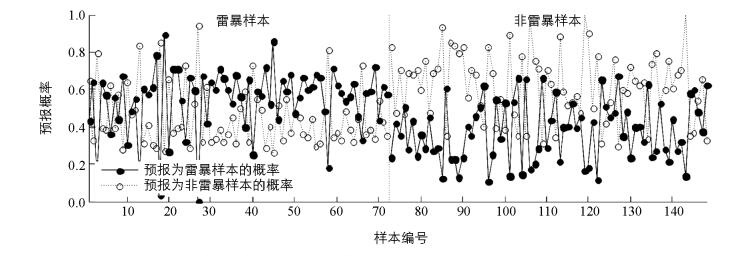
为了验证预报方法的优劣，这里采用独立样本来检验预报结果，并用4个指数作为评估标准，分别是：临界成功指数CSI^[22]、探测概率POD^[23]、虚假报警率FAR^[24]和总指数TS^[25].经多次试验，隐节点数设为7，20，采取两级分类输出，即：当预报该样本为雷暴样本的概率大于预报其为非雷暴样本的概率时，将其预报为雷暴样本，反之为非雷暴样本，预报结果见表 2.

C_CSI，T_TS，F_FAR，P_POD分别为成功指数、探侧概率、虚假报警率和总指数的值.

雷暴是局地强对流天气，其发生发展往往比较迅速，12 h预报模型常常由于实效过长导致预报结果达不到理想效果.因此，为寻求最佳的预报模型，调整实效，尝试建立6 h实效的雷暴潜势预报模型.

因此，908个样本被分为3类，6 h内有雷暴样本276个，6 h以上12 h以内有雷暴样本126个，12 h以内无雷暴样本506个.针对6 h实效，雷暴样本是276个，无雷暴样本是632个，雷暴样本比例30.4%，需要删除一些非雷暴样本来提高雷暴样本的比例，这么做的目的是为了使网络能够掌握每一类样本的特征.处理方法是，6 h以上12 h以内有雷暴样本随机删除一半，12 h以内无雷暴样本随机删除一半，至此，剩余的样本中，雷暴样本276个，非雷暴样本316个，雷暴样本比例达到了46.62%，将这592个样本随机抽取其中3/4用来训练，1/4用来独立检验.这一模型中，训练样本共有444个，检验样本有148个.将样本采取与2.2同样的处理方法进行预处理并建模，得到的双隐层BP网络两层隐节点数分别为16，13，预报结果如表 3.

与12 h实效的预报结果对比发现，6 h实效的预报结果更好，CSI评分提高了3.65%，总指数提高了1.46%，虚假报警率降低7.8%，探测率略有降低，降低2.99%.

通过统计12 h实效双隐层两级输出BP网络预报错误的样本发现：空报的37个样本中探空前1 h发生雷暴的样本有3个，探空前3 h发生雷暴的样本有9个，探空前6 h发生雷暴的样本有13个，这些雷暴的发生对大气电场以及探空因子产生的影响可能还没有消失，容易导致空报.漏报的20个样本中，探空前12 h未发生雷暴，探空后仅发生1次闪电的样本有7个，平均发生在探空后6.4 h.这7次雷暴发生的地点有6个距离探空站在37 km之外，平均距离36.97 km.由于雷暴发生距离探空时间较长，且距离探空站点距离较远，探空时这些因子可能还没有受雷暴影响，容易导致漏报.

同样，统计6 h实效BP网络模型预报错误的样本发现：空报的18个样本中6 h实效前后1 h发生雷暴的样本有5个，6 h实效前后3 h发生雷暴的样本有7个.漏报的17个样本中，探空前6 h未发生雷暴，探空后仅发生1次闪电的样本有5个，平均发生在探空后3.2 h.这5次雷暴发生的地点有4个距离探空站在29 km之外，平均距离26.73 km.

1) 利用和雷暴相关的9个因子：修正总指数、修正K指数、沙氏指数、对流稳定度指数、条件对流稳定度指数、Teffer指数、Charba总指数、瑞士雷暴指数、抬升指数作为辽宁地区雷暴潜势预报的因子.

2) 利用BP人工神经网络模型对雷暴天气进行潜势预报研究，临界成功指数为57.46%、探测概率为79.38%、虚假报警率为32.46%和总指数为74.89%，预报效果较令人满意.

3) 建立12 h和6 h潜势预报BP神经网络模型，通过预报结果对比发现，6h BP神经网络模型更适用于沈阳地区雷暴潜势预报.对预报误差进行初步分析，发现雷暴发生与探空的时间差、距离、雷暴强度、陡度、密集程度都对探空因子产生影响，从而影响预报精度.雷暴临近预报还是需要结合卫星云图、雷达回波等数据进行综合预报来提高预报精度.